让变式“因地制宜”使探究“水到渠成”①
——开放性变式探究教学一例
张宗余
(浙江省象山中学 315700)
1 问题的提出
“使高考复习成为好数学教学”,其具体体现在使学生学会思考,进而学会学习.例题变式探究教学是在教师的指导下,以例题为载体,以学生自主学习和合作讨论为前提,以变式为主要学习手段,为学生提供自由表述、质疑、探讨问题的机会,强调多向互动,教学相长的一种教与学的操作体系. 教学中教师有意识地对数学例题作多层面、多角度的变式与探究,引导学生从“变”的现象中发现“不变”的本质,从“不变”中探求规律,将教学活动营造为开放、宽松、愉悦、和谐的师生探究与合作交流的过程,逐步培养学生灵活多变的创新思维品质,完善学生的认知结构,提高学生发现问题、解决问题和探索创新的能力。但在实践过程中,如何把握变式探究的节奏,使其真正发挥教育功能,是一个值得不断探讨的话题.
2 教学设计及意图
引例在△ABC中,若c2=a2+b2,则△ABC是直角三角形. 若cn=an+bn(n∈N*,n>2),问△ABC为何种三角形,为什么?
设计意图问题是课堂活动的载体,本题是一道难得的好题,综合性强,内涵丰富,横跨几何、三角、代数三学科.而且结论是开放的,给学生思考与探讨的空间.
分析本例条件抽象,先取一些特殊值试探一下.令n=3,a=1,b=1,则c≈1.26,画以(1,1,1.26)为边的三角形草图,易观察知是锐角三角形.上述用特殊值试验的结论具有一般性,师生一起用分析证法.
解因为cn=an+bn(n>2),所以c>a,c>b.由c是△ABC的最大边,需证明C为锐角,只要cosC>0就行了,即证a2+b2>c2.(*)
再注意到条件an+bn=cn,于是将(*)等价变形为(a2+b2)cn-2>cn.
因为c>a,c>b,n>2,
所以cn-2>an-2,cn-2>bn-2,
从而
(a2+b2)cn-2-cn=(a2+b2)cn-2-an-bn
=a2(cn-2-an-2)+b2(cn-2-bn-2)>0,
说明(*)式成立,故cosC>0,C是锐角,△ABC为锐角三角形.
设计意图由特殊到一般的探究法是一种重要的解题思维方法, 与学生一起分析题意,交流解题思路,教师在适当时机给点睛之笔.在分析过程中要注重知识的横向联系,及例题具有的延伸性,挖掘其潜在的内容,进一步一题多变,让变式“顺势而为”.
变式1已知△ABC中,a,b,c分别是∠A,∠B,∠C对应的边,且a2+b2=c2,求证an+bn 设计意图引导学生向更广的范围、更深层次去联想、纵横引申,通过一题多解促进学生知识融会贯通,促进解题能力和思维能力不断提高,形成解题方法和策略. 证1不等式放缩 因为a2+b2=c2,所以c>a,c>b. 又因为n≥3,所以n-2≥1, 所以cn-2>an-2,cn-2>bn-2. 所以c2·cn-2=(a2+b2)·cn-2>a2an-2+b2bn-2, 即cn>an+bn. 证2进行三角换元适当放缩 所以0 所以cnsinnA 所以cnsinnA+cncosnA 即an+bn 证3利用二项式定理的展开式 因为 因为a2+b2=c2, 又因为 所以an+bn 证4构造函数,利用函数的单调性 因为a2+b2=c2,所以c>a,c>b; 因为n≥3,所以f(n) 证5与自然数有关的命题,用数学归纳法证明. ①当n=3时,(因为a2+b2=c2,a>0,b>0,c>0,所以c>a,c>b). a3+b3=a·a2+b·b2 =c·(a2+b2)=c3. ②假设若当n=k时成立,即ak+bk 则当n=k+1时, ak+1+bk+1=a·ak+b·bk =c(ak+bk) 即ak+1+bk+1 综合①②可知当n≥3时,an+bn 设计意图启发同学们从不同角度思考问题,五种解法跨越三角函数,排列组合,函数单调性,数学归纳法等知识板块,起到了很好的复习作用. 同时通过对变式题探讨激发同学们的思维,此时教师要“顺势而动”,让变式探究再进行. 变式2已知 △ABC的三边a,b,c满足 设计意图变式教学诱发一题多解,但解题教学的最终目的是让学生学会思考,通过解法的展示与评价,让学生总结各种方法的优劣,以学会合理地选择,从而快速地、有效地解题.让学生对变式1的多种解法重新审视,找出其中本质的、核心的方法.显然变式1中的证法1、2、3、5都有其局限性,证法4是自然、简单的. 探究1若△ABC的三边长a,b,c满足aα+bα=cα,则a>1或α<0. 证明显然α=0不合题意. 假设0<α≤1,则由已知得cα>aα且cα>bα. 因为y=xα是(0,+)上的增函数, 所以,c>a且c>b. 所以f(1)≤f(α), 亦即a+b≤c. 这与a,b,c是△ABC的三边长矛盾. 所以a>1或α<0. 探究2若△ABC的三边长a,b,c满足aα+bα=cα(α>1),则 1°当1 2°当a=2时,△ABC是直角三角形; 3°当a>2时,△ABC是锐角三角形. 证明因为a>1,aα+bα=cα, 所以c>a,c>b. 已知f(x)是R上的减函数,于是有: 1°当1 所以a2+b2-c2<0,从而cosC<0, 所以C是钝角.故△ABC是钝角三角形; 2°当a=2时,显然cosC=0,所以C是直角,故△ABC是直角三角形; 3°当a>2时, 所以a2+b2-c2>0,从而cosC>0, 所以C是锐角. 故△ABC是锐角三角形. 设计意图数学解题勿忘自然、简单的原则,在探究1、2始终围绕证法4展开,从一题多解到多题一法,深化理性的认识.在例题变式探究教学过程中,“多题一法”是在“一题多解”、“一题多变”基础上的一次提升,更是对核心问题和核心方法的一次提炼.所以也可以引导学生自行解决探究3. 探究3若△ABC的三边长a,b,c满足aα+bα=cα(α<0),则△ABC既可以是锐角三角形,又可以是直角三角形或钝角三角形.(证略) 变式探究应“因地制宜”,不能为变式而变式,为探究而探究,要“顺势而为”。 这里的“地、势”是指学生的认知结构与思维方式,这是变式探究教学的根本.本节课例题选择了开放的视角,从特殊到一般,调动学生学习的兴趣,让学生自主参与分析与研讨。此时学生探究意识已被激发,教师要把原来的题目变成“长流活水”,顺着学生思维发展的方向,利用变式的手段挖掘不断例题的内涵.变式1的设计起点低,却视角丰富,显然为学生进一步探究提供了“把练场”,使学生在引例中引发的思维之花得以尽情绽放,变式诱发了一题多解,这才是课堂教学的魅力所在。 对变式1的解法中引导学生一题多解, 一题多解能重构知识网络,认清知识内在联系,提炼不同的数学思想方法. 而一题多解的目的并不在于“多解”,而在于思维的“多层次”,在于学生从多解中分析出解法的优劣,获得高水平的思维训练,从而提高学生的数学思维能力,培养学生的创新意识.时时不忘提醒学生,是否有更为自然、简单的解题方法呢?探究1与探究2的设计看似从“一题多解”到“多题一法”的跨越,其背后是培养学生从发散思维到聚敛思维,收到“解一题,会一类,同一片”的效果.这样的教学不但培养学生问题意识,发展学生创新思维能力,更重要的是通过变式和自我探究引导学生学会学习和掌握科学方法. 将数学探究活动植根于例题教学活动中,让更多的教学环节渗透探究的元素、探索方法、探究思想,让数学探究真正成为学生学习的习惯.这样才能真正改变学生的学习方式,提高学生的创新能力.当然探究学习过程不是强加于学生,教师应引导学生研究探究对象背景、形成过程及与其他对象之间的联系.让学生真正经历探究的过程,这样探究活动才是真实且自然的.要把握探究内容的难度,创设探究的情境,“惑学生所惑,难学生所难,错学生所错”设身处地地揣摩学生的认知状态,在此基础上因势利导,实现师生“思维共振”,有效地促进了学生的思维的参与,让整个探究过程显得更自然、流畅,让学生在探究中学会探究. “让学生带着问题轻松步入课堂,在愉快且又适度紧张中学习(探究);又要让学生带着新的、更高层次的问题走出课堂,在自由自在中研究(学习)、发展.”这是例题变式探究教学理想化追求,也是实现使高三例题教学成为好数学教学的关键所在。教师要让变式“因地制宜”,学生的探究“水到渠成”,使变式探究教学这朵绚丽的奇葩,在数学教学的百花园争奇斗艳.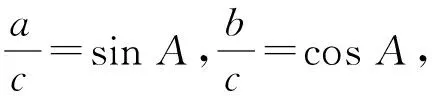
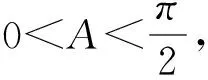
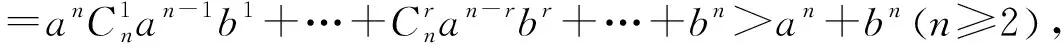

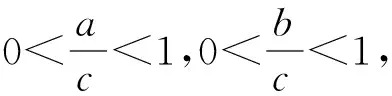
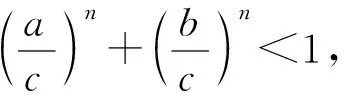
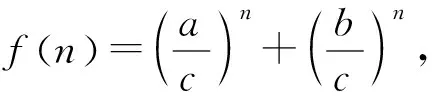
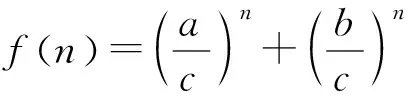
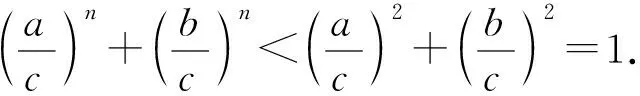
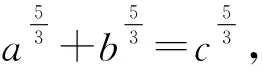
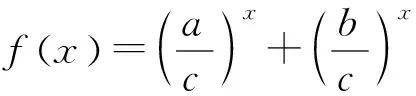
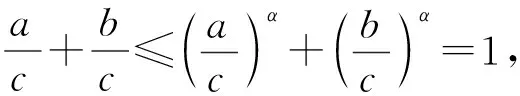
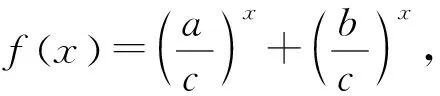
3 几点教学建议
3.1 变式教学诱发一题多解
3.2 解题勿忘自然、简单的原则
3.3 让探究成为一种习惯

