数学问题解答

2017年10月号问题解答

(解答由问题提供人给出)

求证：S△BP1Q1·S△BP2Q2=S△FA1P1·S△FA2P2．

(北京市陈经纶中学 张留杰 100020)

证明如图，连结CF，

因为A1E1∥A2E2，A1E1=A2E2，

又直径BF⊥A1E1于O1，

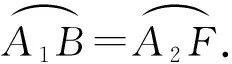
所以∠BCA1=∠FCA2，即∠BCP1=∠FCP2，

∠BCA2=∠FCA1，即∠BCP2=∠FCP1．

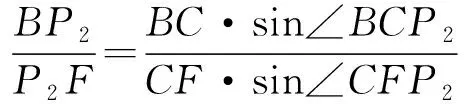
②

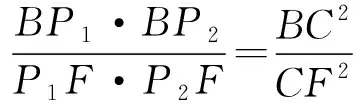
③

因为BF为圆O的直径，所以 ∠BCF=90°，

所以 Rt△BO1Q1～Rt△BCF，

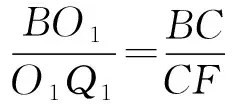
④

⑤

⑥

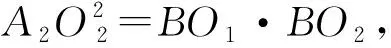
又A1O1=A2O2，

所以A1O1·A2O2=BO1·BO2．

由③和⑥式得

所以(BP1·O1Q1)·(BP2·O2Q2)

=(A1O1·P1F)·(A2O2·P2F)

即S△BP1Q1·S△BP2Q2=S△FA1P1·S△FA2P2．

2387设a,b,c≥0，a+b+c=6，求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

证明不妨设a≥b≥c≥0，则2≥c≥0，先考虑

(1)

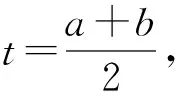
不等式(1)等价于

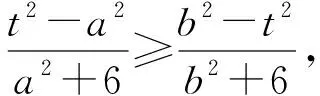
等价于(t+a)(b2+6)≤(b+t)(a2+6)，

等价于6(a-b)≤ab(a-b)+t(a2-b2)，

等价于[(a+b)2+2ab-12](a-b)≥0，

(2)

因为a+b=6-c≥4，

所以(a+b)2+2ab-12≥42+2ab-12>0，

而a≥b，即(2)成立，也就是(1)成立.

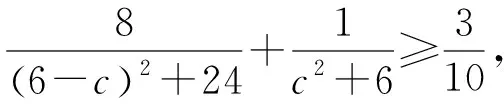
(3)

其中2≥c≥0.

不等式(3)等价于

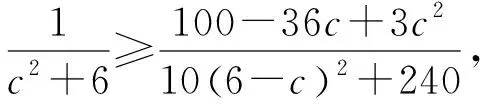
等价于 10(6-c)2+240

≥(c2+6)(100-36c+3c2)，

等价于c4-12c3+36c2-32c≤0，

等价于c(c-2)2(c-8)≤0，

(4)

注意到2≥c≥0，立即知(4)成立.

从以上证明过程，容易知道：当a,b,c都为2，或者a,b,c中一个为0，另两个为3时，所证不等式取得等号.

2388如图，经过直角梯形ABCD的顶点A作斜腰CD的平行线交下底BC于点M，△DBC的外接圆ω1交直线DM于点D,G，△AMC的外接圆ω2交ω1于点C,F，△BGM的外接圆ω3交ω2于点M,E， 证明：直线BE,CF,DG交于一点，且此点为△AMC的重心.

(河南省辉县市一中 贺基军 453600)

证明依题意，只须证明直线BE,CF,DG分别过△AMC的重心.

(Ⅰ)如图，设直角梯形上底AD的延长线与直线BE交于点H.

因∠AMB=∠DCB=∠DGB=∠MGB，

故圆ω3与直线AM相切于点M，

从而有∠EMA=∠EBM=∠EHA，

由此可知A,E,M,H四点共圆，点H在圆ω2上.

因AH∥MC，故圆内接四边形AMCH为等腰梯形.设它的底边MC和AH的中点分别为P,Q，

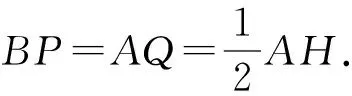
设△AMC的中线AP与直线BH的交点为W，

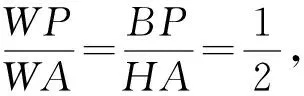
因此W为△AMC的重心，直线BE过点W.

(Ⅱ)在△AMC中，设线段CW的延长线与AM交于点O，并与它的外接圆ω2交于点F′.

作MN⊥AH于点N，则四边形ABMN为矩形，

点O为对角线AM与NB的交点.

因NB=AM=DC，故四边形NBCD为等腰梯形(当N与D重合时该图形为等腰三角形)，它的顶点N,B,C,D共圆，因此点N在圆ω1上.

在圆ω2中，由相交弦定理得

F′O·OC=AO·OM.

因AO·OM=NO·OB，

故F′O·OC=NO·OB，

由此可知F′,B,C,N四点共圆，

点F′在圆ω1上.

这就是说，点F′为圆ω1与ω2的交点，且异于交点C，因此F′,F两点重合，直线CF过点W.

(Ⅲ)因四边形AMCD为平行四边形，故它的对角线MD平分AC，从而可知MD过△AMC的重心W，因此直线DG过点W.

综上，命题得证.

2389在△ABC中，a,b,c；ta,tb,tc；R，r分别表示三边长，内角平分线长，外接圆半径和内切圆半径， 则有

(河南质量工程职业学院 李永利 467000)

证明设△ABC的半周长为p，面积为△，ha,hb,hc分别是三边a,b,c上的高．

先证(1)式左端的不等式：

由三角形内角平分线公式

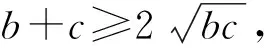
于是，由上面三式、均值不等式、柯西不等式和a+b+c=2p可得

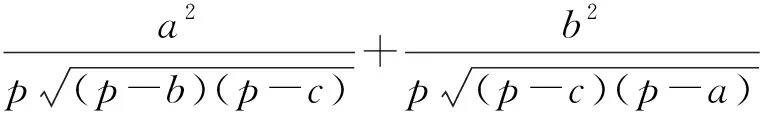
=4，

故(2)式成立．

下面再证(1)式右端的不等式：

由ta≥ha,tb≥hb,tc≥hc和三角形面积公式

及abc=4Rrp，a+b+c=2p可得

故(3)式成立．

由(2)，(3)两式可知不等式(1)成立．

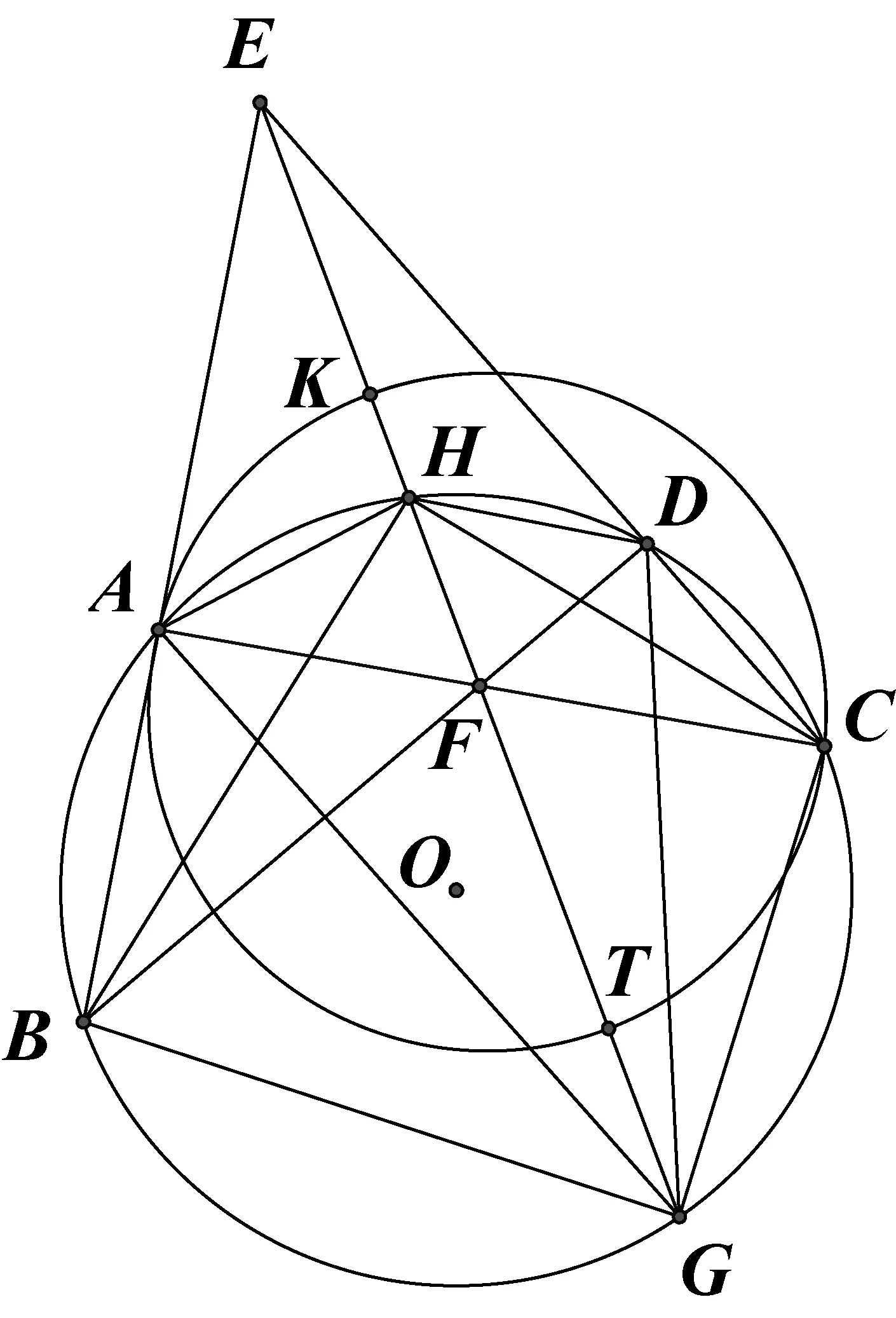
2390如图，已知⊙O上四点A、B、C、D，BA交CD于E，AC交BD于F，EF交⊙O于H、G，K为EF中点，以点A、K、C作圆交EG于T，求证：HF=TG．

(江西师范高等专科学校 王建荣 335000；温州私立第一实验学校 刘沙西 325000)

证明如图，由相交弦定理

KF·FT=AF·FC=HF·FG和EF=2KF，

因此HF=TG

⟺KF·FT+KF·TG=AF·FC+KF·HF

⟺KF(FT+TG)=HF·FG+KF·HF

⟺KF·FG-KF·HF=HF·FG，

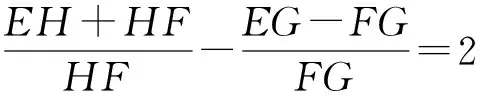
由面积比可知

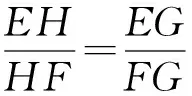
再由正弦定理

故HF=TG．

2017年11月号问题

(来稿请注明出处——编者)

2391凸四边形A1A2A3A4在直线l同一侧，A1A3与A2A4是凸四边形的两条对角线，△A2A3A4,△A1A3A4,△A1A2A4及△A1A2A3的面积分别是S1，S2，S3，S4.Ai至直线l的距离为di(i=1,2,3,4)，则d1S1+d3S3=d2S2+d4S4.

(江苏如皋市老师进修学校 徐道 226500)

2392如图，PAB、PCD分别是⊙O的两条割线，交⊙O于点A、B、C、D，AD与BC相交于点Q.若

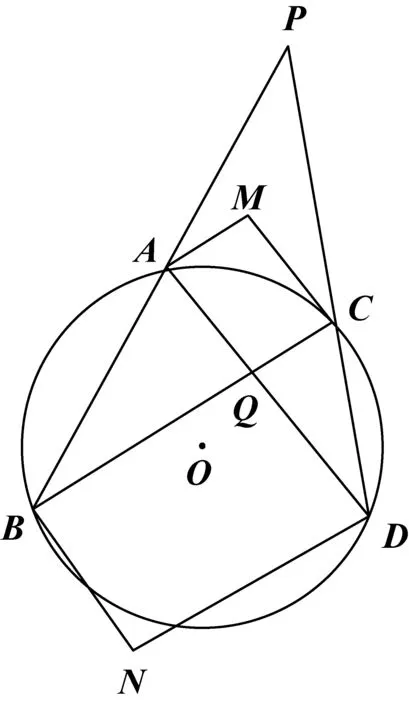
点M、N分别满足四边形MAQC、四边形NBQD都是平行四边形.证明：P、M、N三点共线.

(重庆市合川太和中学 袁安全 401555)

(浙江温州市区马鞍池东路1-408 陈克瀛 325000)

2394在等边三角形ABC中，D为边BC的中点，P为线段BD上异于端点的一点，延长线段AP交该三角形的外接圆于点Q，延长线段QD交AQ的垂直平分线MN于点M,证明：

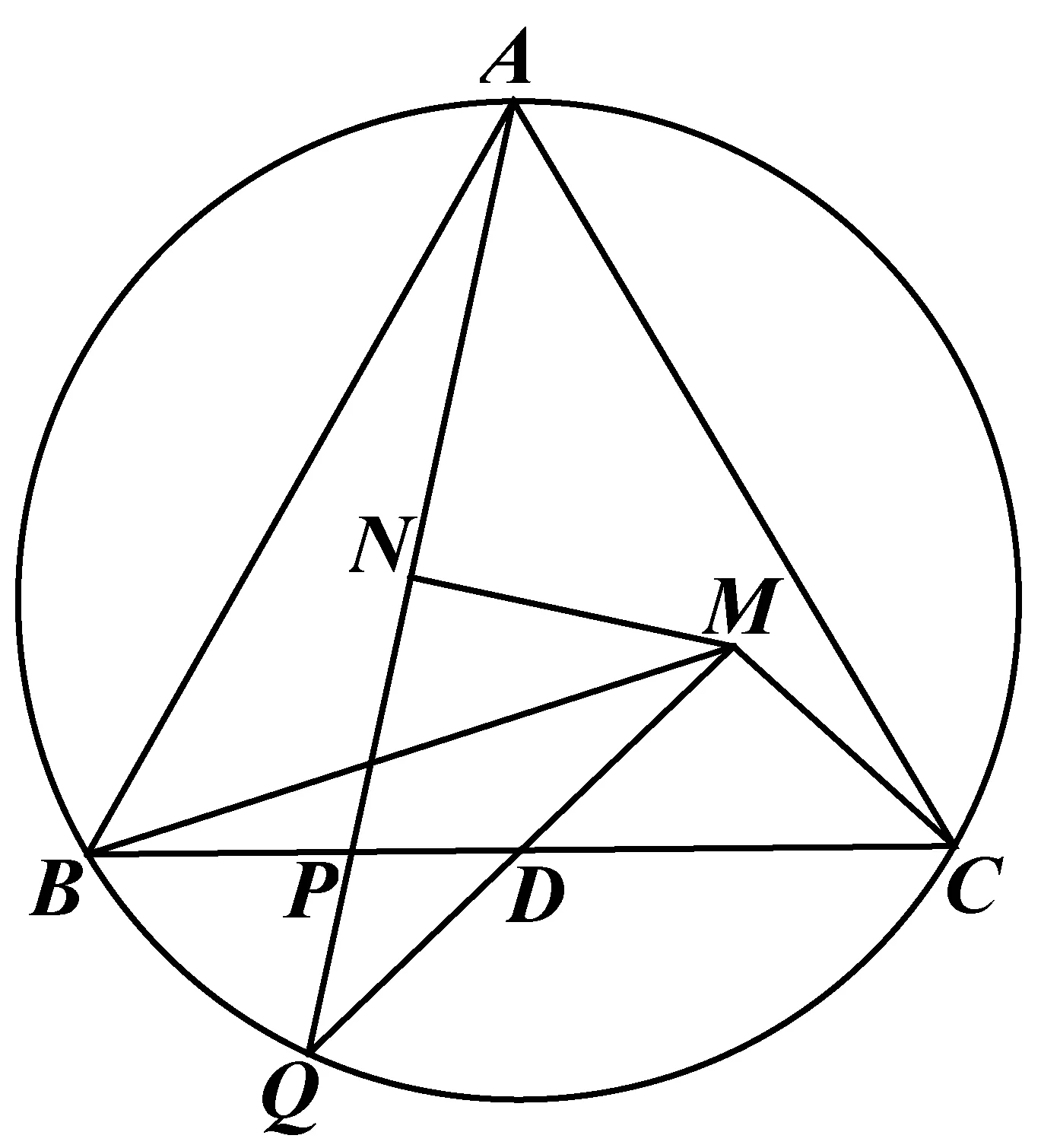
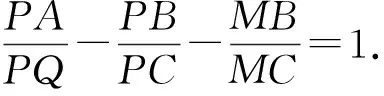
(河南省辉县市一中 贺基军 453600)

2395已知△ABC三边长,面积,半周长,外接圆及内切圆半径分别为a,b,c,△,s,R,r.则

(黄兆麟 天津水运高级技工学校 300456)