数学教学中培养学生发现问题能力的实践①
陆正海 杨子圣
(江苏省泰州中学 225300)
1 问题的提出
“解决问题”是相当长的一段时期及至当下数学教育的重要形式,而《义务教育课程标准(2011年版)》早已将原来总目标中的“解决问题”改为“问题解决”,进行修改的目的是为了更加重视学生问题意识培养,以及解决问题综合能力的培养,强调学生在具体的情境中发现问题、提出问题,提高分析问题和解决问题的能力;修订中的普通高中《数学课程标准》中课程目标进一步明确了通过高中数学课程的学习,“……;提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”);…….”.事实上,在初高中数学课程教学中,提高学生的数学核心素养必须凭借数学化过程,其核心环节就在于,从数学的视角发现问题、提出问题并加以分析和解决.
新课程强调培养学生发现问题和解决问题的能力,强调数学要促进学生的思维发展就应当培养学生的问题意识,只有成功地使学生产生问题的教学,才能真正调动学生的学习积极性.然而在现行的数学教学中,部分老师还是很少为学生提供发现问题、提出问题的平台,仍停留在传统意义上的“老师问学生答”的“解决问题”基本模式上,因此学生没有时间发现问题,也不可能自主发现问题,更谈不上提出问题和解决问题了.由此可见,在初高中数学教学中培养学生发现问题的能力是使学生获得数学核心素养的重要途径,应该成为数学教师教学设计的出发点和教学行为转变的方向.
2 培养学生发现问题能力的策略与方法
数学教学中要使学生产生学习的兴趣,就要精心创设教学情境,吸引学生的注意力,激发其求知欲与好奇心,激发学生对数学知识学习的热情,进而引导学生自己发现问题、提出问题,拉近学生与新知识的距离,让学生真正成为学习的主人.如何培养学生发现问题和解决问题的能力呢?
2.1 概念教学中提出问题
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产生、发展、应用的过程中.通过高中数学课程的学习,学生能在情境中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验;养成在日常生活和实践中一般性思考问题的习惯,把握事物的本质,以简驭繁.因此,数学抽象思维训练是培养学生提出问题能力的重要途径和方法.
例1向量及其运算的教学
向量和物理学有着密切的联系,物理学研究的基本对象之一是矢量,矢量是既有大小又有方向的量.如力、位移、速度、加速度、动量、电场强度等,这些量贯穿于物理学的许多分支,矢量是现实存在的,可以观察、感受到的,物理学中的矢量是向量的现实模型;向量的加法运算可以以位移的合成为背景;向量的数乘运算以位移或速度的倍数为背景,可使学生对数与向量的数乘运算的结果仍然是向量有直观的认识;两个向量的数量积运算以力所做的功为背景.所以,向量及其运算是物理学中矢量及运算的抽象,教学中应引导学生从物理情境中抽象出数学概念和问题,培养学生的问题意识、创新意识和应用意识.
2.2 数学理论建构过程中提出问题
抽象建立起来的数学概念和理论,其不断发展完善过程的教学也是培养学生发现问题、提出问题的重要途径.
例2一脉相承的共线向量定理和平面(空间)向量基本定理
共线向量定理:共线的的向量可选择其中一个非零向量为基向量,用它可以表示共线的任一向量,即若b∥a,且a≠0,则有且只有一个实数λ,使b=λa.
事实上因为b∥a,

而唯一性常用反证法,
若又有b=λ′a(λ′≠λ),
则λ′a=λa,(λ′-λ)a=0,
|(λ′-λ)a|=0,|(λ′-λ)|·|a|=0,
因为a≠0,所以|a|≠0,
所以(λ′-λ)=0,
即λ′=λ与假设λ′≠λ矛盾,
故λ是唯一的.
说明:
(1)非零向量a可看成所有共线向量的基向量;
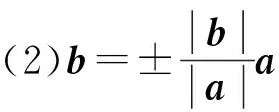
①单位化a;②乘以|b|;③确定符号.
共线的的向量可选择其中一个非零向量为基向量,用它可以表示共线的任一向量,那平面内、空间内的向量,是否有相应的理论呢?水到渠成地引导学生提出了新的问题.
例3有心二次曲线的“垂径定理”
下面的图形是从圆的两个性质定理引导学生提出椭圆和双曲线(有心二次曲线)的类似性质问题的示意图(图中M是弦AB中点或曲线上一点,有关斜率存在时).
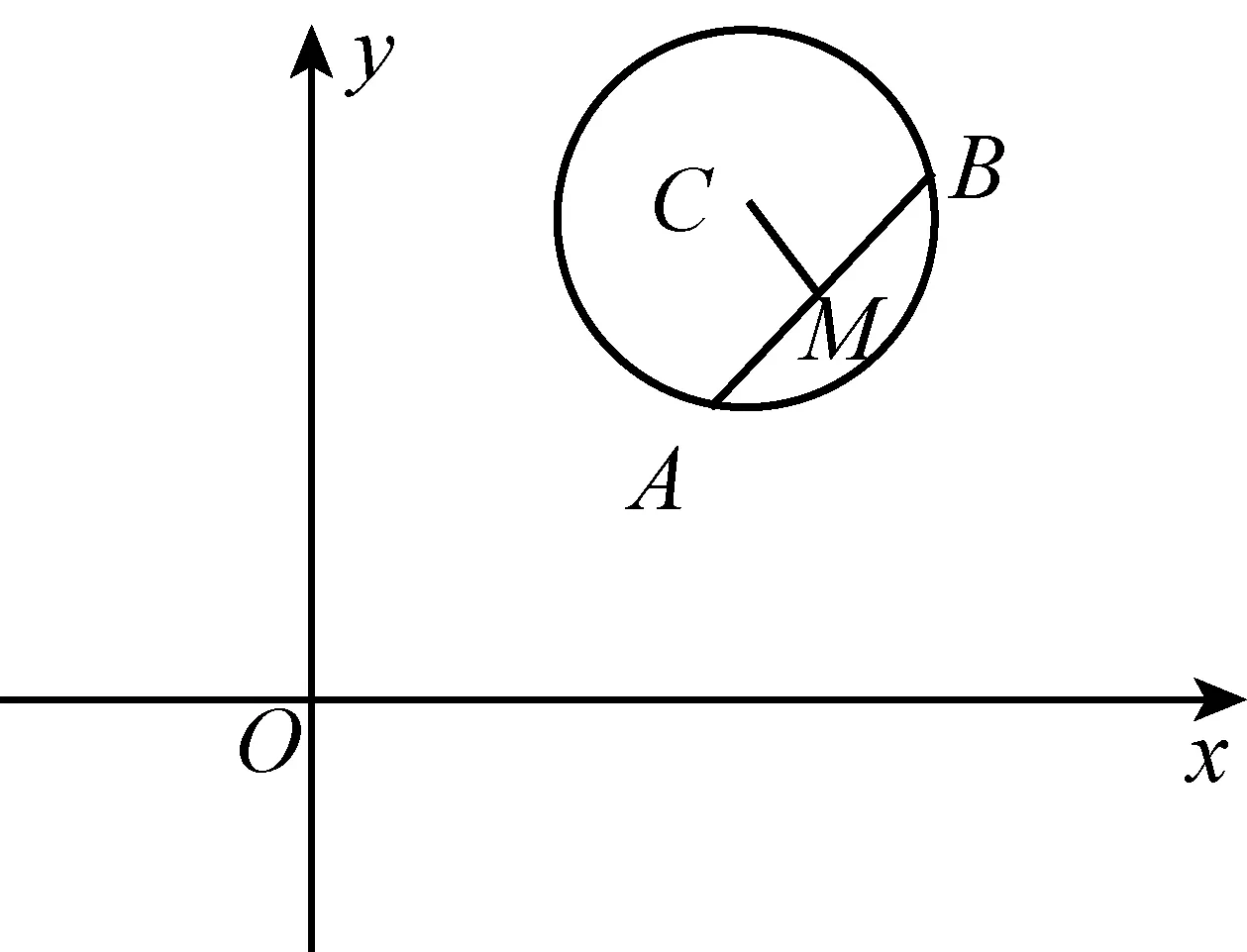
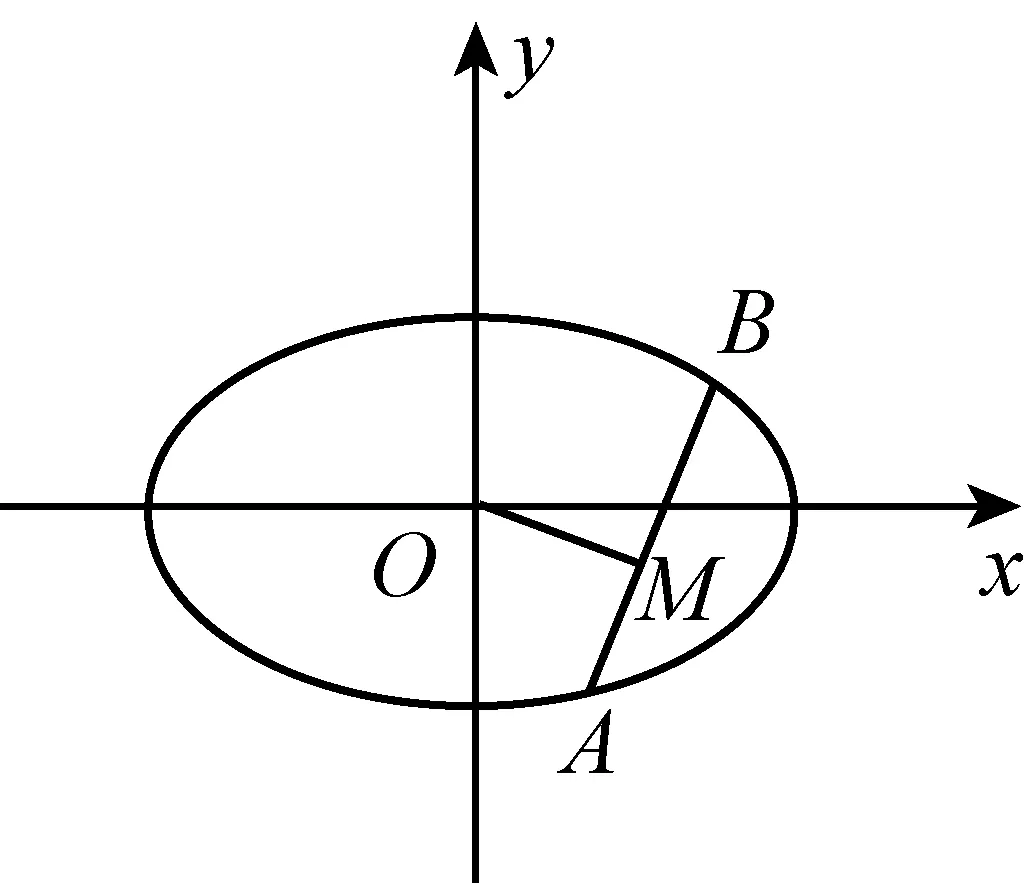
(x-a)2+(y-b)2=R2⟹mx2+ny2=1,(mn≠0)

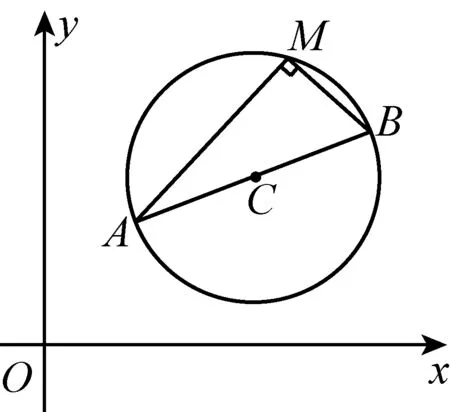
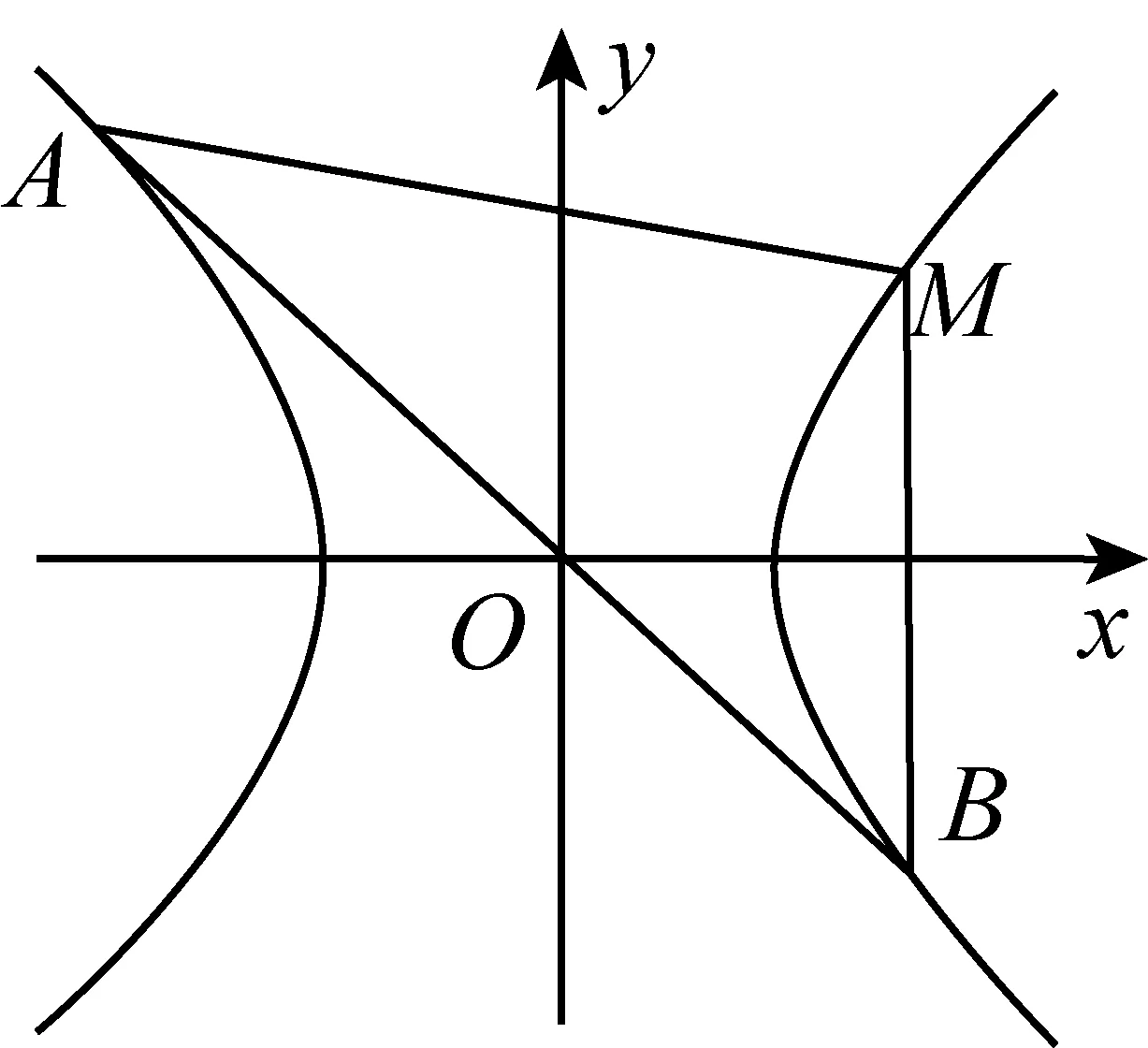
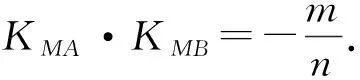
这里的本质其实就是通过类比思维发现问题提出问题,这样的情形在我们平常的教学中比比皆是,自然也是很重要的培养学生发现问题、提出问题的途径.
2.3 数学问题解决的过程中提出问题
数学问题解决是一种积极探索和克服障碍的活动过程,它所采用的途经和方法是新的,至少其中某些部分是新的,这些方法和途径是已有数学知识和方法的重新组合,这种重新组合通常构成一些更高级的规则和解题方法,因此数学问题解决的过程又是一个发现和创新的过程.
例4“设而不求”在导数应用中的运用
导数应用的所有问题都以研究导函数f′(x)的零点, 即方程f′(x)=0的解为基础, 当断定方程f′(x)=0有解, 但又发现其解不能求或不易求时, 就可引导学生提出新的解题构想,即“设而不求 整体代入”的方法.
已知函数f(x)=xex-1,g(x)=lnx+kx,若f(x)≥g(x)对任意x∈(0,+∞)恒成立,求实数k的最大值.
解由f(x)≥g(x)分离参数得
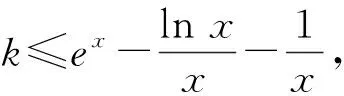
则k≤h(x)min,
显然x>0时,函数x2ex+lnx单调递增,
值域为R,有唯一的零点,但不可求,
这时发现问题并引导学生提出新的解决问题的思路和方法, 即“设而不求”方法.
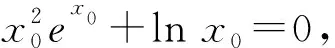
且x∈(0,x0)时,h′(x)<0,h(x)递减,
x∈(x0,+∞)时,h′(x)>0,h(x)递增,
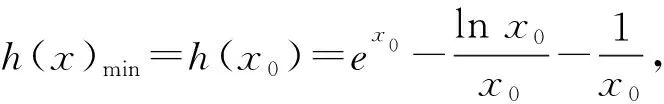
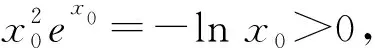
2lnx0+x0=ln(-lnx0),
lnx0+x0=ln(-lnx0)+(-lnx0),
而函数lnx+x单调递增,

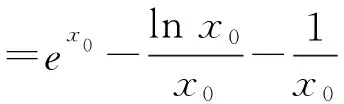
所以k≤1,k的最大值为1.
例5一道填空题的解法探究
在平面直角坐标系中,圆C1:(x+1)2+(y-6)2=25,圆C2:(x-17)2+(y-30)2=r2.
若圆C2上存在一点P,使得过点P可作一条射线与圆C1依次交于点A、B,满足PA=2AB,则半径r的取值范围是____________.[5,55]

学生以及教辅资料中有关这道题的很多解法都是利用特殊情形和极限情形得到答案的,教学中应引导学生发现这类解法的问题并提出如何给出严谨的解法.
设C1到直线PA的距离C1M=d,
由PA=2AB,得PM=5AM,

从而圆C2与C3有公共点,则不等式组
对0≤d<5能成立,
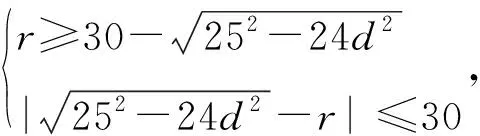
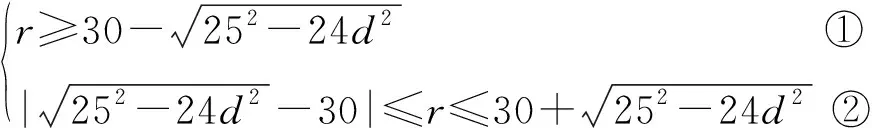
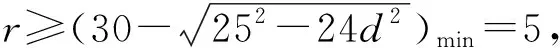
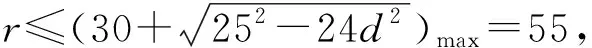
所以5≤r≤55.
可见,这样的解题反思也是发现问题、提出问题的重要途径.
3 结束语
数学新课程强调培养学生发现问题和解决问题的能力,强调数学要促进学生的思维发展就应当培养学生的问题意识,只有成功地使学生产生问题的教学,才能真正调动学生的学习积极性.长期的数学问题解决学习,能培养学生用数学的眼光去观察身边的事物,用数学的思维方法去分析日常生活中的现象.在数学问题解决过程中学生还能切身感受到运用数学知识解决问题后的成功体验,这不仅可以增强学生学好数学的信心,还可以使他们更加深刻地感受到自己所学的数学知识都是有用的.在教学中挖掘数学问题解决中隐藏的培养学生探索精神和创新能力的巨大潜力,引导学生加强数学问题解决的学习,充分发挥其培养学生探索精神和创新能力的功能,是培养学生数学核心素养、实施素质教育的必然要求.

