数学问题2313号的简证与探究

欧阳熙琴

(江西省赣州师范高等专科学校 341000)

在△ABC中，记BC=a,CA=b,AB=c,其半周长、面积分别为p、S;ra,rb,rc,ma,mb,mc,wa,wb,wc,ha,hb,hc分别是△ABC对应边上的旁切圆半径、中线、内角平分线、高．

《数学通报》2016年第7期刊登2313号问题：

经笔者探究发现三角形的中线、内角平分线及高线也有以上有趣性质．即

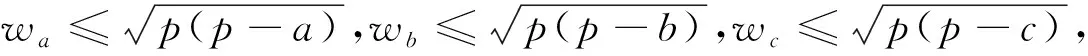
由Heron公式知 2∑a2b2-∑a4=16S2，

又据平凡不等式 ∑a4≥∑a2b2，

得 ∑a2b2-16S2=∑a4-∑a2b2≥0，

其实上述过程就是对问题2313号的简洁证明．

由权方和不等式得

定理1得证．

从而得ma≥wa，同理得mb≥wb，mc≥wc，又据熟知的wa≥ha，wb≥hb，wc≥hc，由此得到一个优美的不等式链：

笔者进一步通过研究得到如下更一般结果．

定理2对于n∈N+且n≥2,我们有

证明由幂平均不等式及权方和不等式得

则

旁切圆半径、中线与高线的证明仿内角平分线，故略．