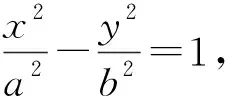对一道解析几何高考题的推广

储今雨

(北京师范大学附属中学 100052)

高中遇到的很多解析几何题，特别是一些证明题，给人的感觉总是充满了机缘巧合.通过学习分析探究这些题目，发现所给的条件往往都是一般问题的特殊化处理.一些看似简单的条件，往往都是做了精心的设计.因此在解题过程中，对所给条件内在联系的把握至关重要.

下面以2017年全国高考北京卷理科的第18题为例，对题目条件相关问题进行了探究，以揭示看似简单的条件背后的秘密.

(Ⅰ)求抛物线C的方程，并求其焦点坐标和准线方程；

(Ⅱ)求证：A为线段BM的中点．

解(Ⅰ)略.

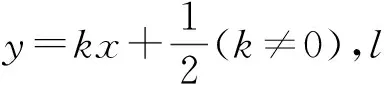
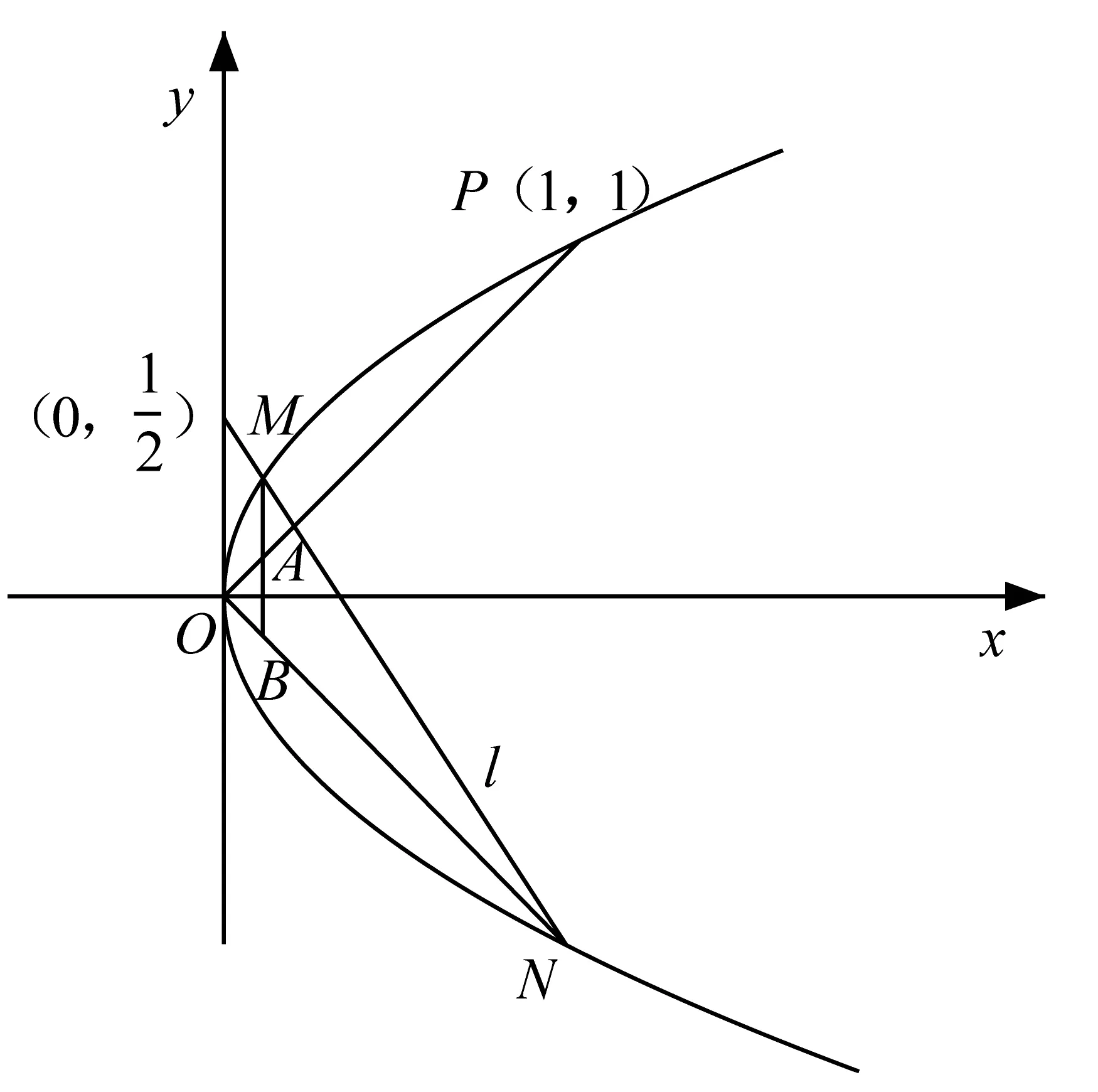
图1

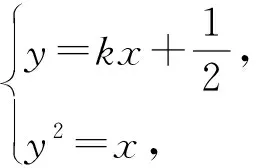
得4k2x2+(4k-4)x+1=0．

因为点P的坐标为(1,1)，

所以直线OP的方程为y=x，

点A的坐标为(x1,x1)．

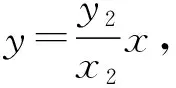
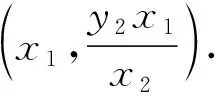
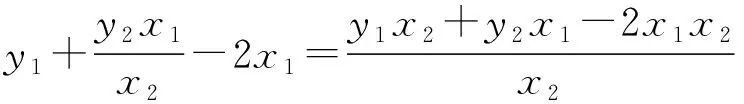
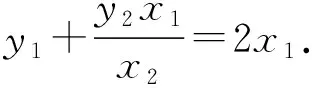
故A为线段BM的中点．

分析设直线的方程为y=kx+b(k≠0)，

得k2x2+(2kb-1)x+b2=0．

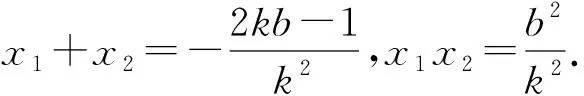
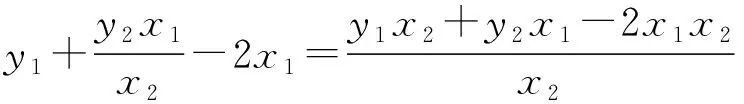
也就是当点P(1,1)不变时，D换成y轴上除原点外的其他点，结论就不成立了，因此抛物线的方程是由点P(1,1)决定的，这说明D与P之间是有联系的.

探究2过点D作直线l与抛物线C交于不同的两点M,N，点M,N是否会与点P重合呢？

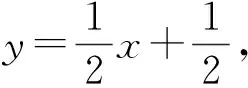
也即直线DP与抛物线C只有一个交点，所以点M,N不会与点P重合.

探究3解决了上述两个问题，对题目条件作进一步分析：直线DP与抛物线C只有一个交点，等价于直线DP是抛物C线的切线.那么能否从切线的角度将点D的范围推广呢？也就是对于抛物线C:y2=2px，过y轴上除原点外的任意一点D作抛物线的切线DP，若其他条件不变，A为线段BM的中点的结论仍成立吗？

分析设D(0,b)，直线l的方程为y=kx+b(k≠0)，

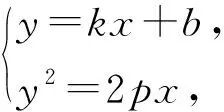
得k2x2+2(kb-p)x+b2=0．

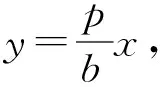
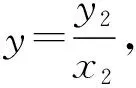
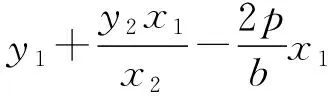
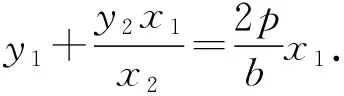
故A为线段BM的中点．

由此可得出：

推广1已知抛物线C:y2=2px，过y轴除原点外的任意一点D作抛物线的切线DP，切点P，过点D作直线l与抛物线C交于不同的两点M,N，过点M作x轴的垂线分别与直线OP,ON交于点A,B，其中O为原点．则A为线段BM的中点.

探究4再将点D的范围作进一步的推广：对于抛物线外任意点D，是否有类似的结论成立？原题中的其他条件是否也要变化？原题中点A,B是过点M作x轴的垂线分别与直线OP,ON的交点，与x轴垂直的直线也可以看作是与y轴平行的直线.从抛物线的角度来看，y轴是切线，O是切点，所以当点D推广时，过点D作抛物线的两条切线，点A,B是过点M作与一条切线平行的直线分别与直线QP,QN的交点，A还是线段BM的中点吗？

分析设D(x0,y0)，当x0=0时，已证明.下面证明x0≠0的情况，设切点Q(x3,y3),P(x4,y4)，此时y0y3y4≠0.如图2，直线DQ的斜率一定存在，则直线DQ:y3y=p(x+x3)，

直线DP:y4y=p(x+x4)，

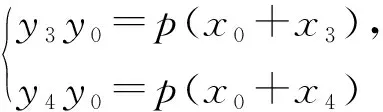
解得2px0=y3y4，2y0=y3+y4.

①

直线PQ:y0y=p(x0+x)，

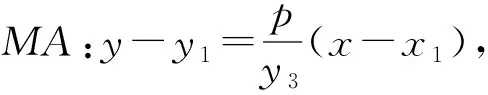
因为D，M,N在一条直线上，

所以(y1-y0)(x2-x1)=(y2-y1)(x1-x0)，

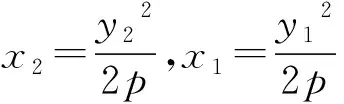
图2

得(y1-y0)(y2+y1)=2p(x1-x0)，

化简得y1y2-y0y2-y0y1+2px0=0，

将①代入得

(y1+y2)(y3+y4)=2y1y2+2y3y4

②

若证明A为线段BM的中点，只要证明点M关于A的对称点A′在直线QN上.A′在直线QN上等价于

(yA′-y3)(x2-x3)=(y2-y3)(xA′-x3)，

即证 (yA′-y3)(y2+y3)=2p(xA′-x3)

③

又xA′=2xA-x1

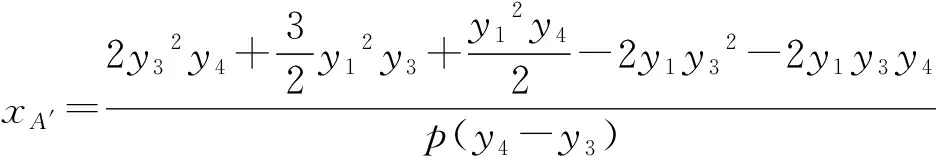
2y32y4+y3y12+y4y12-y32y1-y32y2-2y12y2+3y1y2y3-3y1y3y4+y1y2y4-y2y3y4=0

④

原命题就是证明上式恒成立.

左边变形为

(y3-y1)(2y3y4+2y1y2)+y1(y1y3+y2y3+y1y4+y2y4)-y3(y1y3+y1y4+y3y2+y2y4)

把②变形为y1y3+y2y3+y1y4+y2y4=2y1y2+2y3y4

显然④成立，因此猜想得证.

由此得出：

推广2已知抛物线C:y2=2px，过抛物线外任意一点D作抛物线的两条切线，设切点为P,Q，过点D作直线l与抛物线C交于不同的两点M,N，过点M作与DQ平行的直线与直线PQ,QN交于点A,B，则A是线段BM的中点.

探究5类似地，如果把抛物线换成椭圆和双曲线，同理可证类似结论仍成立.由此可得到以下两个结论: