对一类三元n次不等式的证明

杨学枝

(福建省福州第二十四中学 350015)

以下四个定理可用于证明一类三元n次不等式.文中“∑”与“∏”分别为三元数的循环和与循环积.

定理一若①λ,u≥v≥0，w≥0；②(λ-1)(λ-w)≤0，(u-1)(u-w)≤0(或λ,v≥u≥0，w≥0，(λ-1)(λ-w)≤0，(v-1)(v-w)≤0；或u,v≥λ≥0，w≥0，(u-1)(u-w)≤0，(v-1)(v-w)≤0)；③(λ-1)(λ-w)+(u-1)·(u-w)+(v-1)(v-w)≤0；④λ+u+v≤1+2w.则对于n∈N，n≥2，有

λn+un+vn≤1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

证明为以下书写方便，记

fk(p,q)=pk+pk-1q+pk-2q2+…+qk(k=0,1,2,…)，并约定f0(p,q)=1，则

λn+un+vn-1-2wn

=(λn-1)+(un-1)+(vn-1)-2(wn-1)

=(λ-1)fn-1(λ,1)+(u-1)fn-1(u,1)+

(v-1)fn-1(v,1)-2(w-1)fn-1(w,1)

≤(λ-1)fn-1(λ,1)+(u-1)fn-1(u,1)+

(v-1)fn-1(v,1)-[(λ-1)+(u-1)+

(v-1)]fn-1(w,1)

(应用④)

=(λ-1)[fn-1(λ,1)-fn-1(w,1)]+(u-1)[fn-1(u,1)-fn-1(w,1)]+

(v-1)[fn-1(v,1)-fn-1(w,1)]

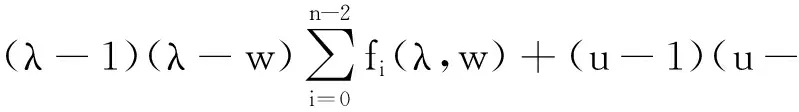
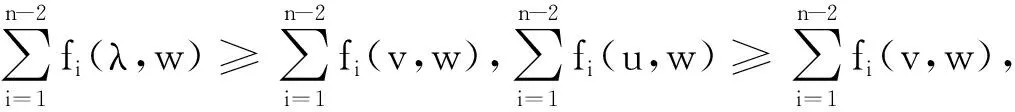
应用③，即得原式.

推论一若①λ,u,v,w≥0；②(λ-1)(λ-w)≤0，(u-1)(u-w)≤0；(v-1)(v-w)≤0；③λ+u+v≤1+2w.则对于n∈N，n≥2，有

λn+un+vn≤1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

同理可证以下三个定理(证略).

定理二若①0≤λ,u≤v，w≥0；②(λ-1)(λ-w)≥0，(u-1)(u-w)≥0(或0≤λ,v≤u，w≥0，(λ-1)(λ-w)≥0，(v-1)(v-w)≥0；或0≤u,v≤λ，w≥0，(u-1)(u-w)≥0，(v-1)(v-w)≥0)；③(λ-1)(λ-w)+(u-1)(u-w)+(v-1)(v-w)≤0；④λ+u+v≤1+2w.则对于n∈N，n≥2，有

λn+un+vn≤1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

定理三若①λ,u≥v≥0，w≥0；②(λ-1)(λ-w)≥0，(u-1)(u-w)≥0(或λ,v≥u≥0，w≥0，(λ-1)(λ-w)≥0，(v-1)(v-w)≥0；或u,v≥λ≥0，w≥0，(u-1)(u-w)≥0，(v-1)(v-w)≥0)；③(λ-1)(λ-w)+(u-1)(u-w)+(v-1)(v-w)≥0；④λ+u+v≥1+2w.则对于n∈N，n≥2，有

λn+un+vn≥1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

推论二若①λ,u≥v≥0，w≥0；②(λ-1)(λ-w)≥0，(u-1)(u-w)≥0；(v-1)(v-w)≥0；③λ+u+v≥1+2w.则对于n∈N，n≥2，有

λn+un+vn≥1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

定理四若①0≤λ,u≤v，w≥0；②(λ-1)(λ-w)≤0，(u-1)(u-w)≤0(或0≤λ,v≤u，w≥0，(λ-1)(λ-w)≤0，(v-1)(v-w)≤0；或0≤u,v≤λ，w≥0，(u-1)(u-w)≤0，(v-1)(v-w)≤0)；③(λ-1)(λ-w)+(u-1)(u-w)+(v-1)(v-w)≥0；④λ+u+v≥1+2w.则对于n∈N，n≥2，有

λn+un+vn≥1+2wn，

当且仅当λ,u,v有一个等于1，其余两个及w都相等时取等号.

下面举数例说明以上定理的应用.

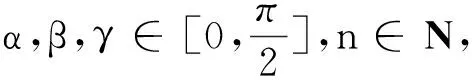
∑cos2n(β-γ)≤1+2∏cosn(β-γ)(1)

当且仅当α,β,γ中有两个相等时，式(1)取等号.

cos2(β-γ)≥cos2(α-γ)≥0，

cos2(α-β)≥cos2(α-γ)≥0，

∏cos (β-γ)≥0,

满足定理一中条件①.

另外，由于

cos2(β-γ)-1≤0；

cos2(β-γ)-∏cos (β-γ)

=cos (β-γ)[cos (β-γ)-cos (α-γ)cos (α-β)]

=cos (β-γ)sin (α-γ)sin (α-β)

≥0，

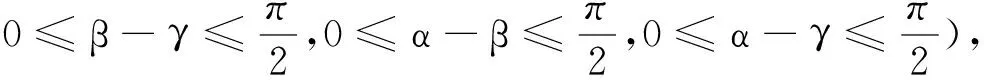
因此，有

[cos2(β-γ)-1][cos2(β-γ)-∏cos (β-γ)]≤0，

同理，有

[cos2(α-β)-1][cos2(α-β)-∏cos (β-γ)]≤0,

满足定理一中条件②.

[cos2(β-γ)-1][cos2(β-γ)-∏cos (β-γ)]

+[cos2(α-γ)-1][cos2(α-γ)-∏cos (β-γ)]

+[cos2(α-β)-1][cos2(α-β)-∏cos (β-γ)]

=-sin2(β-γ)sin (α-γ)sin (α-β)cos (β-γ)

+sin (β-γ)sin2(α-γ)sin (α-β)cos (α-γ)

-sin (β-γ)sin (α-γ)sin2(α-β)cos (α-β)

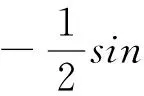
=-2sin2(β-γ)sin2(α-γ)sin2(α-β)≤0,

满足定理一中条件③.

又由于

∑cos2(β-γ)-[1+2∏cos (β-γ)]

=[cos (β-γ)-cos (γ-α)cos (α-β)]2-[1-cos2(γ-α)][1-cos2(α-β)]

=sin2(γ-α)sin2(α-β)-sin2(γ-α)sin2(α-β)=0，

即有

∑cos2(β-γ)=1+2∏cos (β-γ)，

满足定理一中条件④.

因此，由定理一知原命题成立，并知当且仅当α,β,γ中有两个相等时，式(1)取等号.

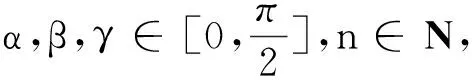
(2)

当且仅当α,β,γ中有两个相等时，式(2)取等号.

证明显然,当α,β,γ中有两个相等时，式(2)取等号，原命题成立.下面对α,β,γ互不相等情况，证明原式成立.

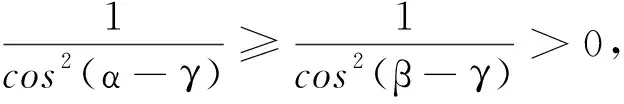
满足定理四中条件①.

另外，由于

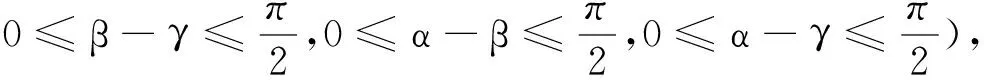
因此，有

同理，有

满足定理四中条件②.

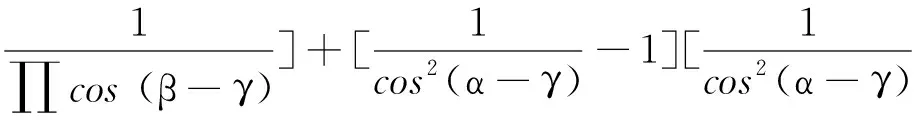
=∏tan (β-γ)[∑tan (β-γ)+∑tan3(β-γ)]

=∏tan (β-γ){∑tan (β-γ)+[∑tan (β-γ)]3

-3∑tan (β-γ)∑tan (α-γ)tan (α-β)

+3∏tan (β-γ)}

=∏tan (β-γ){∏tan (β-γ)+[∏tan (β-γ)]3

-3∏tan (β-γ)∑tan (α-γ)tan (α-β)

+3∏tan (β-γ)}

=[∏tan (β-γ)]2{4+[∏tan (β-γ)]2

-3∑tan (α-γ)tan (α-β)}

=[∏tan (β-γ)]2{4+[∑tan (β-γ)]2

-3∑tan (α-γ)tan (α-β)}

=[∏tan (β-γ)]2[4+∑tan2(β-γ)

-∑tan (α-γ)tan (α-β)]≥0

(注意应用等式∑tan (β-γ)=∏tan (β-γ)),

满足定理四中条件③.

又由于

[1-∏cos (β-γ)]

(注意应用等式

∑cos2(β-γ)-2∏cos (β-γ)=1)

=∑tan2(β-γ)+2∏tan (β-γ)∑cot(β-γ)

(注意应用等式

=∑tan2(β-γ)+2∑tan (γ-α)tan (α-β)

=[∑tan (β-γ)]2≥0,

满足定理四中条件④.

因此，由定理四知原命题成立，并知当且仅当α,β,γ中有两个相等时，式(1)取等号.

例3(自创题)设x,y,z∈R+，n∈N，n≥2，则有

(3)

当且仅当x,y,z中有两个相等时，式(3)取等号.

证明由对称性，不妨设x≥y≥z>0，则

满足定理一中条件①.

另外，由于

≤0,

同理,有

满足定理一中条件②.

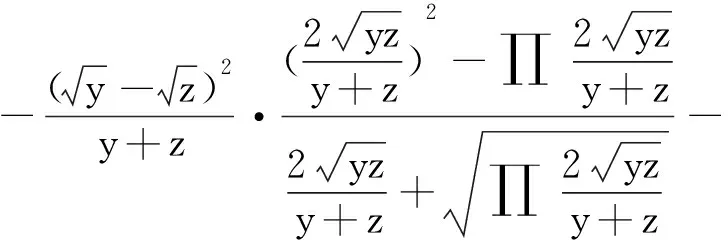
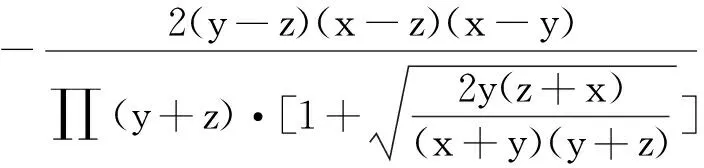
(注意到当x≥y≥z>0时，有

(注意到当x≥y≥z>0时，有

≤0,

满足定理一中条件③.

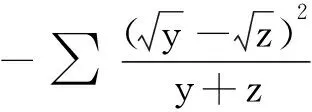
由此可知,我们只要证明

≥0,

≥0，

≥0，

≥0，

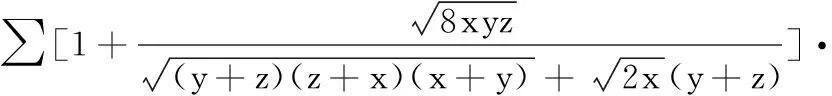
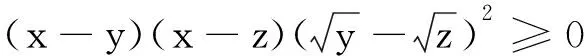
由于x≥y≥z>0，则有

因此，式(※)左边式子

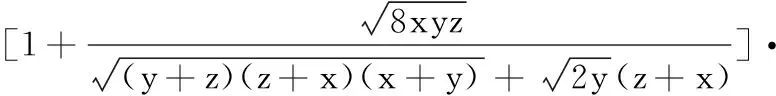
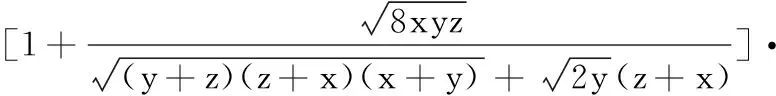
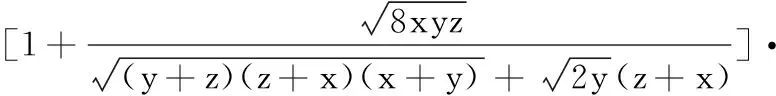
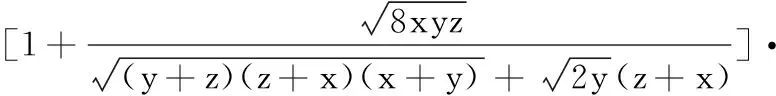
因此，要证明式(※)，只要证明

上式容易证明，事实上，有

≥0，

于是式(※)得证，因此得到

满足定理一中条件④.

因此，由定理一知原命题成立，并知当且仅当x,y,z中有两个相等时，式(3)取等号.

类似证法，若利用定理四，可得

例4(自创题)设x,y,z∈R+，n∈N，n≥2，则有

(4)

当且仅当n=2，或x,y,z中有两个相等时，式(4)取等号.

由例3，例4可得以下不等式链

例5(自创题)设△ABC三边长为BC=a,CA=b,AB=c,其对应边上的中线分别为ma,mb,mc，面积为△，n∈N，则

(5)

当且仅当△ABC为等腰三角形时，式(5)取等号.

证明不妨设a≥b≥c>0，则

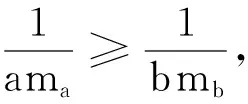
另外,由于2△≤ama,同时有

=(b2c2+c2a2+a2b2)-a2(2b2+2c2-a2)

=(a2-b2)(a2-c2)≥0,

因此,

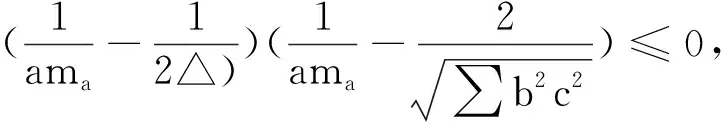
同理可得

满足定理一中条件②.

(注意到在a≥b≥c>0时，上面已证有bmb≥ama，bmb≥cmc)

=0,

满足定理一中条件③.

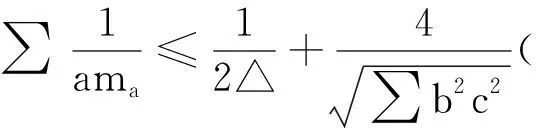
因此, 由定理一知原命题成立，并知当且仅当△ABC为等腰三角形时，式(5)取等号.

利用本文中的定理还可以证明许多类似不等式，这里就不再赘述了.