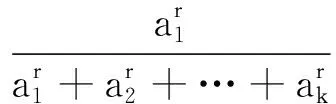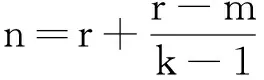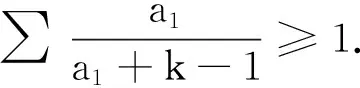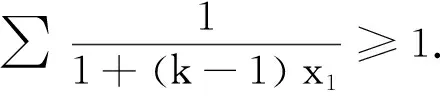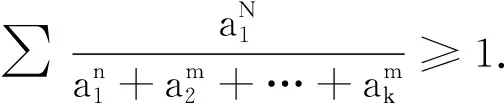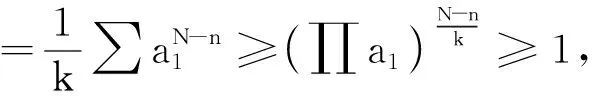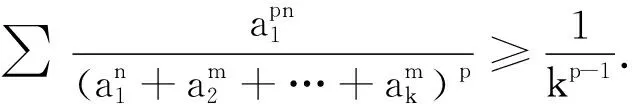对一个数学问题的推广探究
储百六
(安徽省岳西中学 246600)
1 引言
《数学通报》2016年第11期上刊登的2332号问题,笔者通过研究发现该不等式不仅可以推广到一般情况,还可以类比得出很多有意思的不等式,先整理如下.
数学通报第2332号问题:
已知a,b,c,d>0,且abcd=1,求证:
2 问题的推广
2.1 在探讨之前先证两个引理
引理1若ai>0(i=1,2…,k),n≥m≥0,则
证明不妨设a1≤a2≤…≤ak,则有
由Chebyshev不等式可得
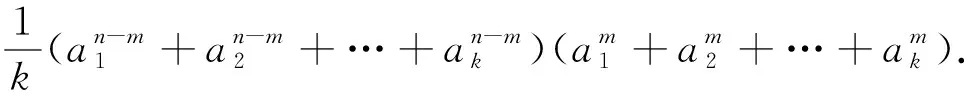
引理2若ai>0(i=1,2…,k),∏ai≥1,i=1,2,…,k,n≥m≥0,则
可由引理1和均值不等式易得.
2.2 问题的推广
定理1设ai>0,且∏ai≥1,i=1,2,…,k(k≥3,k∈N),n>m且n>-(k-1)m,
证明先待定指数r,由引理1和均值不等式可得
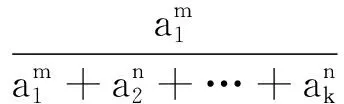
上式成立只需n>r>0,
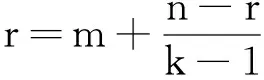
显然n>r>0,于是有
①
类似可得其他式子.所以
证毕.
注1.当k=4,m=0,n=1时,即为数学通报第2332号问题.
2.当k=3,m=0,n=1时,该不等式为2000年澳门地区数学奥林匹克竞赛试题.
3.当k=3,m=-1,n=5时,该不等式为1996年IMO试题.
推论设ai>0,且∏ai≥1,i=1,2,…,k(k≥3,k∈N),n≥m≥s≥0,
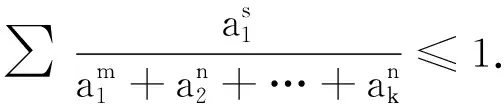
证明由定理1证明中的①式可得
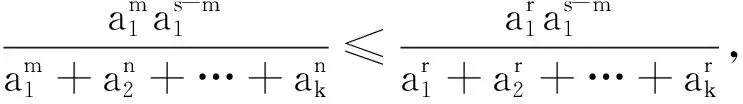
所以
上式最后一步是由引理2推出,
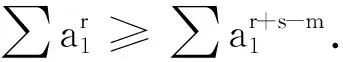
类比定理1可得:
(2)管线埋设于地下,处于隐蔽状态,为确定位置可用管线探测仪、雷达等多种探测方法。目前,业内开始借助潜望镜进行管线探测。潜望镜主要用于井、涵洞,以及暗沟暗区管线探测,在不需人员进入的情况下可以直观观察到内部构造和线路情况,同时也保证了人员下井的安全。潜望镜在排水管线专业中可更好地发挥探测作用,而且还可以直观查看排水管线的内部构造和淤积堵塞情况,为排水管线的隐患排查显示出更大的作用。
定理2设ai>0,且∏ai≥1,i=1,2,…,k(k≥3,k∈N),0≤m 证明先待定指数r,由引理1和均值不等式可得 上式成立只需r>m>0, 于是有 ② 所以 证毕. 注当m=0,n=1时,可得: 从上述证明中的②式,由引理1还可将定理2推广为: 推广1设ai>0,且∏ai≥1,i=1,2,…,k(k≥3,k∈N),0≤m 证明由②式可得 推广2设ai>0,且∏ai≥1,i=1,2,…,k(k≥3,k∈N),0≤m 证明将②式两边p次方可得 于是由幂平均不等式可得