主动变式探究 体验数学发现——以一道向量题的变式教学为例

顾日新

(苏州工业园区星海实验中学 215021)

荷兰著名数学教育家汉斯·弗赖登塔尔认为：数学教育方法的核心是学生的“再创造”，他反复强调：学习数学的唯一正确的方法是“再创造”，也就是由学生本人把要学的东西在实践中发现或创造出来，教师的任务是引导和帮助学生进行这种再创造的工作，而不是把现成的知识直接灌输给学生．反思当前习以为常的变式教学，教师始终是变式的主体——提出问题，学生只是被动的接受——解决问题，对于为什么要进行变式或者如何进行变式，学生一概不清楚，学生的“再创造”难以实现，创新精神难以培养．本文以一道经典的向量高考题为例，尝试引导学生对题目的条件加以变化，在实施变式探究的过程中，体会变与不变的辩证思想，体验数学创造、数学发现的历程．现摘部分教学简录，敬请同行及专家斧正．

1 经典真题回顾

(2008浙江卷·理9)已知a、b是平面内两个互相垂直的单位向量．若向量c满足(a-c)·(b-c)=0，则|c|的最大值是( )(答案：C)

A．1 B．2

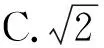
评注：这道题看似简单，其实内涵丰富，堪称经典．

2 教学简录

2.1 解法探究——体现向量的数、形交融

师：分析题目的条件，大家想到了什么方法？

生1：题设中出现了单位向量，以及两组向量垂直，我觉得可以用几何法解决．

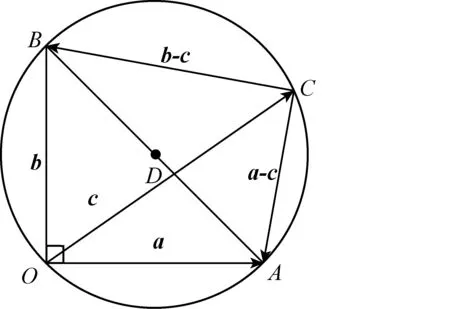
图1

师：你善于抓住题设特征，合理运用了数量积为0的几何意义，得出点C在以AB为直径的圆上，数形结合，简洁明了．还有不同方法吗？

生2：由于a、b是平面内两个互相垂直的单位向量，所以可以考虑用坐标法进行转化．设a=(1,0),b=(0,1),c=(x,y)，由(a-c)·(b-c)=0得

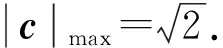
师：和生1一样，你也是转化的高手．用坐标表示向量，得点(x,y)的轨迹是一个圆(原点在圆上)，|c|的最大值即为圆的直径，思路清晰，运算简便．

生3：将等式(a-c)·(b-c)=0直接展开，得c·(a+b)=c2．设a+b与c的夹角为θ,

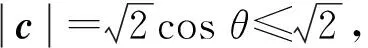
师：引入向量a+b与c的夹角为θ，得到|c|关于θ的三角函数，函数思想的运用恰到好处．比较三种解法，生1、生2的解法体现了向量“形”的神韵，生3的解法则体现了向量“数”的特征．

2.2 变式探究——透过现象看本质

师：变式最为常见方法是改变题目的非核心条件．分析本题的两个条件.

条件1：a、b是平面内两个互相垂直的单位向量；

条件2：向量c满足(a-c)·(b-c)=0.

哪一个条件是核心条件？

生4：条件2．

师：理由？

生4：条件2的几何意义是点C在以AB为直径的圆上，这是解题的关键，但是它和条件1没有关系．

师：你的分析很精辟，你想如何变式？

生4：改变向量a、b的夹角．变式如下：

变式1已知a、b是平面内两个夹角为60°的单位向量．若向量c满足(a-c)·(b-c)=0，则|c|的最大值是．

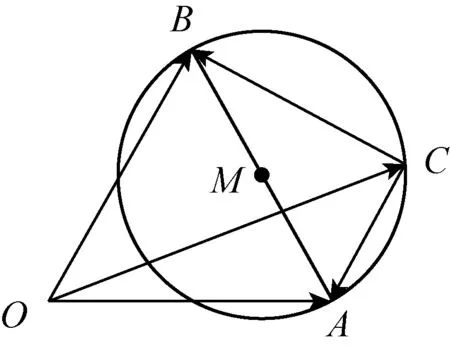
图2

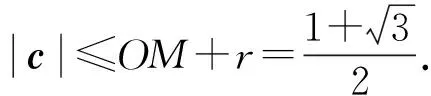
师：改变向量a、b的夹角，不改变向量a、b的模．还可以怎么变？

生5：向量a、b的模和夹角同时改变．变式如下：

变式2已知a=(-1，2)，b=(3，6)．若向量c满足(a-c)·(b-c)=0，则|c|的取值范围是．

解设c=(x,y) 由(a-c)·(b-c)=0得

(x-1)2+(y-4)2=8.

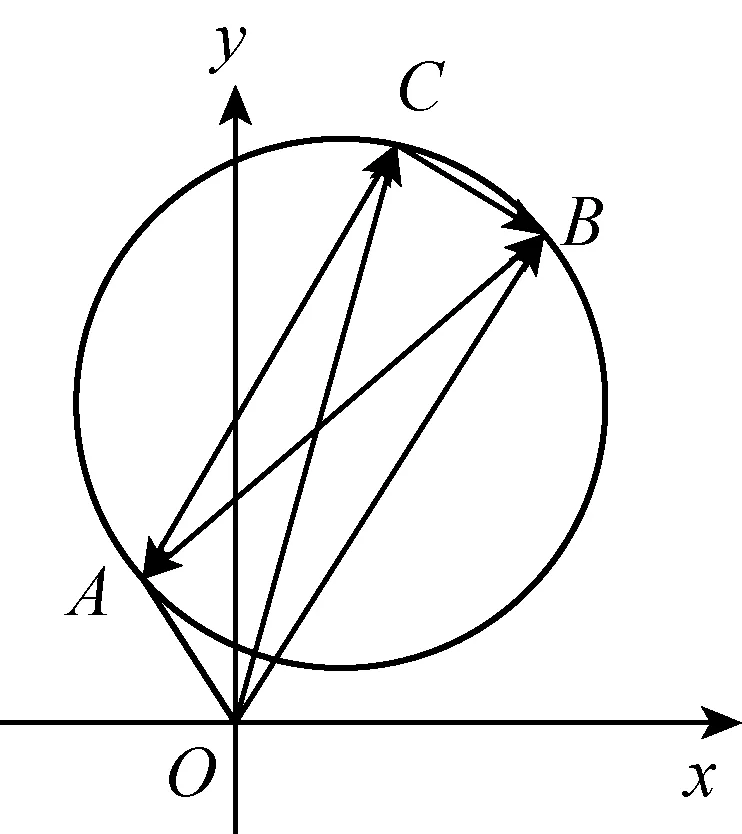
图3

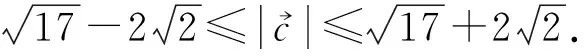
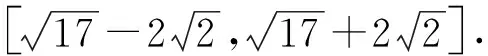
师：相对变式1，变式2对条件1的改变更为彻底．在不改变核心条件(a-c)·(b-c)=0的前提下，改变条件1中a、b两个向量的模和夹角．借助数量积为0的几何意义，或者对向量解析化，把向量模的问题化归为定点到定圆上动点的距离问题．以形助数，简洁明了！ 尽管变式1，变式2对向量a、b的模或夹角进行的改变，但是向量a、b仍然是确定的，从而点C所在的圆也始终是一个定圆，定圆是比较好处理的．还有更大胆的变式吗？

生6：还可以不给定向量a、b的夹角，定圆变动圆．变式如下：

变式3已知a、b是平面内两个单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是．

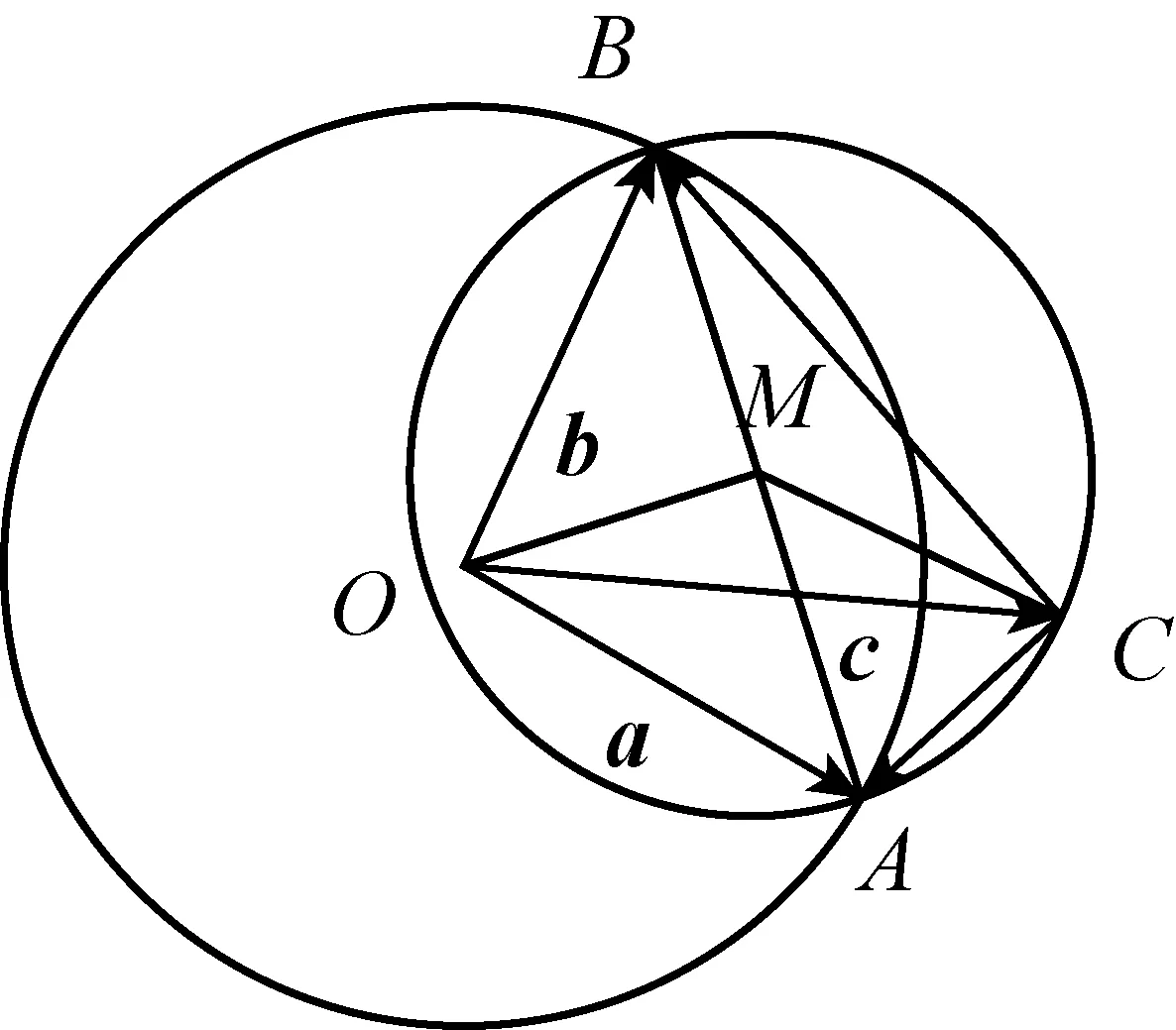
图4

(当且仅当O、M、C共线，且OM=MC时取等号，此时a与b垂直.)

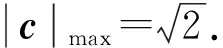
师：非常棒！由于a、b的夹角任意，点C所在的圆随着点A、点B的变化而变化．若设出向量的坐标，尽管思维量小、方向单一，但运算繁琐；而根据数量积为0的几何意义，易得点C的运动轨迹，再巧妙借助三角不等式及基本不等式的推论，问题迎刃而解．反观前文高考真题，该题其实就是变式3的一种特殊情形．通过刚才的变式过程，我们发现，只要核心条件 “(a-c)·(b-c)=0”不变，无论a、b的夹角如何变化，点C始终在一个圆上．那么，条件2能变吗？

生7：向量a-c与向量b-c不一定非要垂直．变式如下：

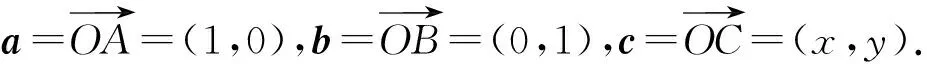
师：很好！尽管向量a-c与向量b-c不垂直，但是向量c仍然和圆有关．还有不同的变式吗？

生8：除了改变向量垂直的属性外，还可以改变条件2中向量前面的系数．变式如下：

变式5已知a、b是平面内两个互相垂直的单位向量．若向量c满足(2a-c)·(b-2c)=-1，则|c|的取值范围是．

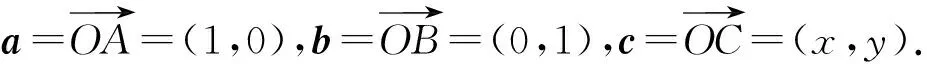
师：通过上面的5个变式，不难发现，向量c始终与某个圆有关，特别是生8的变式5特别有启发性．同学们能提出一个更具有一般性的问题吗？

2.3 提出问题——发现一般规律

经过学生讨论，师生完善，共同提出以下问题：

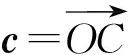
解设a=(x1,y1)，b=(x2,y2)，c=(x,y)，代入(ma+c)·(nb+c)=t，得

x2+y2+(mx1+nx2)x+(my1+ny2)y+

mn(x1x2+y1y2)-t=0

令D=mx1+nx2,E=my1+ny2,

F=mn(x1x2+y1y2)-t

则D2+E2-4F=(mx1+nx2)2+(my1+ny2)2-4[mn(x1x2+y1y2)-t]

=(ma-nb)2+4t.

当(ma-nb)2+4t<0时，点C的轨迹不存在；

当(ma-nb)2+4t=0时，点C为一定点；

当(ma-nb)2+4t>0时，点C的轨迹为圆.

排除(ma-nb)2+4t≤0的特殊情况，得到下述有用的结论：

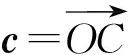
3 教学反思

3.1 重视变式探究的教学功能

变式教学是对学生进行数学技能和思维训练的重要方式，通过对数学问题进行多角度、多方面的变式探究，有意识地引导学生从了解到理解，从变的现象中发现不变的本质，从不变的本质中探索普遍规律．许多研究(黄荣金，2000；鲍建生、黄荣金、易凌峰，顾怜沉，2002；)认为变式训练“看似简单重复，其实是不断求新变化，通过逐渐积累，甚至由量变到质变，得到新的认识”(张奠宙、李士铸、李俊，2003；等)[1]．变式探究不仅能增强学生的创新意识和应变能力，而且能优化学生的思维品质，培养发现问题和解决问题的能力和素质．

3.2 重视变式探究主客体的转换

苏霍姆林斯基认为，在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者，研究者，探索者．变式探究作为一种教与学的方式，其落脚点最终应该落在学生的学，而不是教师的教．从高中生的生理和心理特点来看，每个学生都有探索和创造的潜能，关键是如何激发他们学习的兴趣、动机和求知欲．所以，让学生充当变式的主体不失为一种培养学生“再创造”、培养学生发现问题、提出问题能力的重要手段．此时，教师的作用主要体现在三个方面，一是选择一个好的问题，这是变式探究的基础；二是善于启发和引导，发挥“脚手架”的功能，激发学生在深层次思维中去探究；三是给予欣赏和鼓励，增强学生信心，激发其内驱力，挖掘学生的潜能．

3.3 重视数学思考的教学

对学生而言，数学教学肩负着传授数学知识，发展数学能力，锻炼数学思维，提高数学素养的重任．新课标解读则认为，数学思考是数学教学中最有价值的行为，数学教学要围绕教学生数学思考展开，努力改变一味的模仿，机械重复的训练．何为数学思考，简而言之就是用数学的方式思考问题，其中提出问题，探究发现是数学思考的重要组成部分．课堂教学要关注学生数学思考的过程，更好的唤起数学学习的好奇心，激发并维护学生主动学习、自主学习的积极性．重视数学思考，教师是真正的执行者和落实者．

总之，如果把凸显学生的主体参与性落实到每一节课堂教学中去，那么，培养学生提出问题、发现问题的能力，重视学生数学思考，以学生的发展为本就不再是一个空乏的话题．