基于休眠机理的三维小基站蜂窝网络能效优化∗
潘子宇 胡晗 杨洁
1)(南京工程学院通信工程学院,南京 211167)
2)(南京邮电大学,江苏省无线通信重点实验室,南京 210003)
基于休眠机理的三维小基站蜂窝网络能效优化∗
潘子宇1)2)†胡晗2)杨洁1)
1)(南京工程学院通信工程学院,南京 211167)
2)(南京邮电大学,江苏省无线通信重点实验室,南京 210003)
小基站蜂窝网络,能量效率,休眠机理,泊松点过程
1 引 言
随着无线通信的发展,小基站逐渐成为当前以及未来5G蜂窝网络[1]的重要组成部分.小基站通常部署在写字楼、商贸区等城市密集区域以弥补传统宏基站在覆盖和传输方面的不足[2].一般而言,小基站网络的规划部署是根据高峰时的网络负荷设计的,这必然导致在网络负荷较低时的资源浪费以及不必要的能量消耗[3].因此,蜂窝网络能效优化成为无线通信领域的一个热点课题[4].
动态基站休眠机理是实现蜂窝网络能效优化的有效方法[5].文献[6]介绍了一系列基站休眠方法,如传统休眠、随机休眠、动态休眠和最优休眠机理.文献[7]针对同构蜂窝网络,提出在关闭一定宏基站后通过调节剩余激活宏基站的发射功率以确保开关宏基站前后系统覆盖性能不变.上述优化方法都是基于连接和覆盖约束条件,没有考虑信道容量方面的约束,而信道容量是衡量无线网络质量的一个非常重要的因素[8].文献[9,10]提出了一种基于服务质量(quality of service,QoS)的最优基站密度,从而实现网络能效优化,其QoS约束条件为目标用户的下行信道容量(下行最大传输速率)依一定概率达到预定目标值.这种能效优化是基于“基站覆盖区内所有用户平分系统带宽而没有任何链接数量的限制”这一假设进行的,而实际无线网络中基站接入的用户数是有限制的.文献[11]提出了小区的方法,根据负载情况动态地调整小区尺寸.文献[12]提出了一种联合优化基站休眠概率和发射功率以实现网络能耗最低的方法,并应用于宏基站场景,取得了较好的效果,但其约束条件仅为覆盖概率.文献[13]将文献[12]的优化方法应用于小基站场景,分析了小基站的最优休眠概率问题.上述蜂窝网络不论其网络组织架构是单层形式还是异构形式,其能效优化都是基于二维泊松点过程(two-dimensional Poisson point process,2D PPP)模型[14].小基站通常以较高密度设置在写字楼、商贸区等城市密集区域,呈现立体分布特性,传统的2D PPP模型不能准确地描述小基站的实际分布.文献[15]开创性地将传统的2D PPP模型推广到三维,形成三维泊松点过程(three-dimensional Poisson point process,3D PPP),并将其应用于小基站网络的下行干扰建模和覆盖概率分析,结果比传统的2D PPP模型准确.但是,下行信道容量的估算和能效优化工作在文献[15]中并未涉及,这需要做进一步研究.
本文在文献[15]的基础上推导了基于三维泊松点过程的小基站蜂窝网络下行信道容量的数学表达式,并分析其单调特性.讨论了在平均接入率(average connection ratio,ACR)和下行信道容量双重约束下的最优休眠概率问题,以及基站最大连接数这一重要参数的最佳配置值.该参数的最佳配置能够在ACR和信道容量双重约束下最大程度地降低网络能耗.仿真结果表明,提出的休眠机理对三维小基站网络的能效优化非常有效,基站最大连接数的最佳配置可以为运营商优化网络提供参考.
2 系统模型
2.1 蜂窝网络模型
在三维小基站网络中,小基站和用户的分布分别以齐次泊松点过程(Poisson point process,PPP)Φc和Φu来描述,其密度参数分别为λc和λu.假设用户通信基站的选取遵循最大接收功率原则,即每个用户选择与其距离最近的基站进行通信.不失一般性,考虑目标用户位于坐标原点,其接收信噪比为
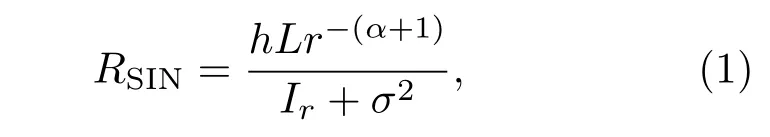
式中h为目标用户与其通信基站间的小尺度衰落(服从瑞利分布);L为室内无线信道衰落系数,由第一米损耗和Devasirvatham室内路径损耗模型[16]共同确定;r为目标用户与其通信基站间的距离;α∈(2,5)为路径损耗指数;σ2为归一化的加性噪声功率;为累计干扰(除通信基站b0以外的所有基站的干扰之和),gi和Ri分别为目标用户与第i个干扰基站之间的小尺度衰落(同样服从瑞利分布)和距离.假设h和gi都是独立同分布的随机变量,且h,gi∼exp(1).考虑4G无线通信场景中一般采用正交频分复用(orthogonal frequency division multiplexing,OFDM)调制[17],本文仅考虑小区间干扰而不考虑小区内干扰.
2.2 平均接入率
文献[6]详细推导了基于平面模型的无线蜂窝网络ACR的数学表达式,本文将此推广到三维立体模型.
在基站休眠机理场景下,处于激活状态的小基站密度记作λc,act,λc,act≤λc.在三维立体空间中,小基站的覆盖区域大小记为A,其概率密度函数为[18]

式中K=5[18],Γ(K)为伽马函数,a为随机变量.根据用户的PPP分布特性,大小为A的小区内的用户数量N服从如下分布:

因此,位于基站覆盖范围内的用户数(记为N)服从如下分布:
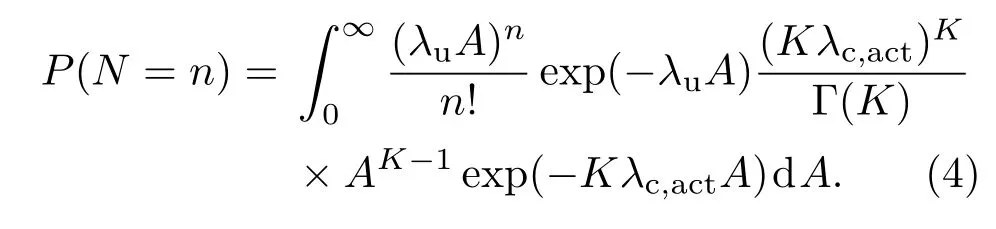
为了保证通信质量,基站连接的用户数量是有限制的[19].假设在多用户连接场景下,每个基站最多可以连接δ(δ>1)个用户,并且所有连接的用户平均分配系统带宽.记Nb为基站连接的用户数,其期望可以表示为[3]
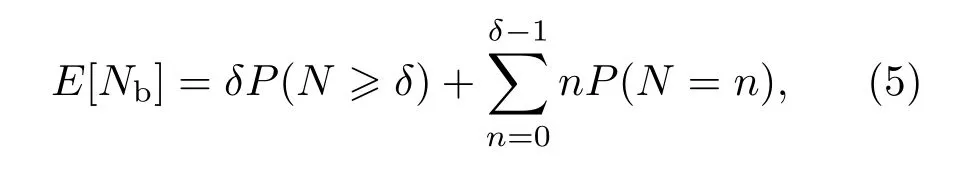
由此,ACR可表示为
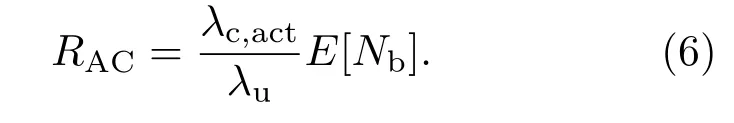
引理1基站平均连接用户数E[Nb]是关于λc,act的单调递减函数.
证明根据(5)式,E[Nb]可展开为


令λc,actA=t,x=λu/λc,act,则

根据复合函数的单调性规则,只需证明

是关于x的单调递减函数即可.
令y对x求导,可得
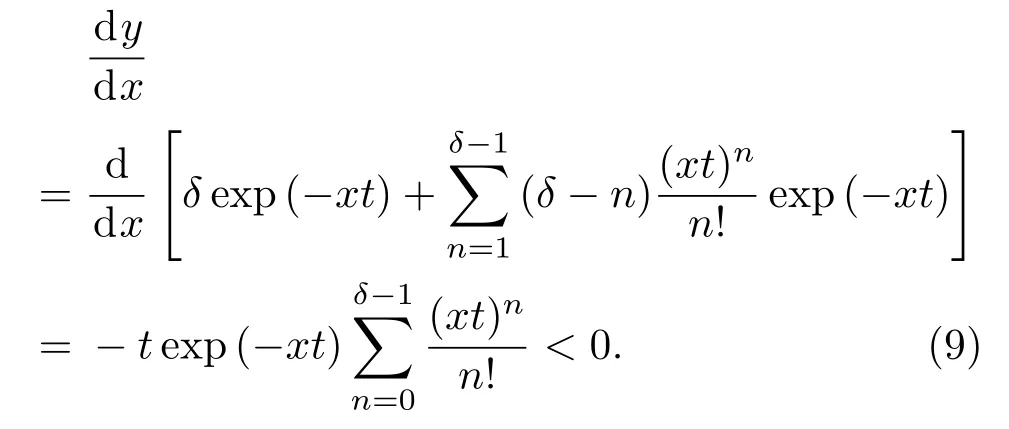
证毕.
3 下行信道容量
首先推导单位带宽下的下行信道容量(即频谱效率[20],单位为bit·s−1·Hz−1)并分析其单调特性,然后给出在实际系统带宽和多用户连接场景下的下行信道容量的数学表达式.
定理1三维小基站网络下行信道容量为


其中
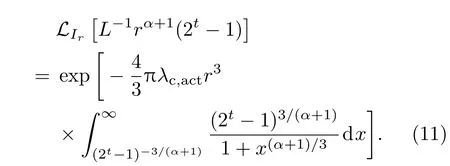
证明根据香农定理、3D泊松分布特性[15]以及瑞利衰落特性,可得

根据h∼exp(1),(12)式中P{h>L−1rα+1×(σ2+Ir)(2t−1)}可展开为

根据文献[15]以及gi∼exp(1),(13)式中的L[L−1rα+1(2t−1)]可展开为

令u=(v/r)3并代入(14)式,可得

将(15)式代入(13)式,即可得到(10)式.
证毕.
特例:在无噪声环境下,即σ2=0,C0(λc,act,α)可简化为
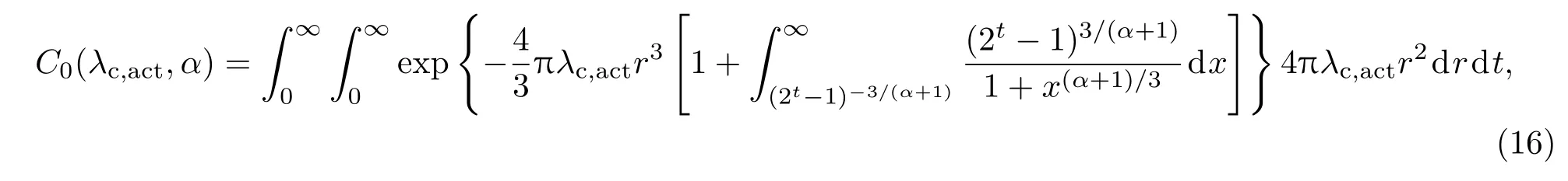
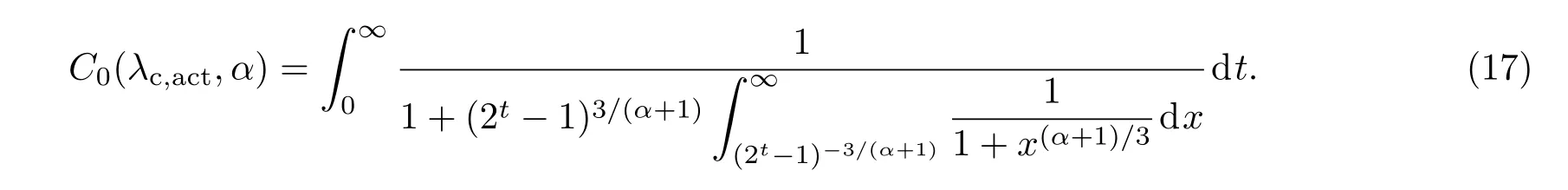
从(17)式可以看出,在无噪声环境下,下行信道容量C0与处于工作状态的小基站的密度无关.一般情况下,路径损耗指数α=4.因此,在无噪声环境下,信道容量C0可通过两次数值积分计算得到,C0(λc,act,4)≈1.61 bit·s−1·Hz−1.
推论1在噪声环境下,即σ2>0,C0(λc,act,α)是关于λc,act的单调递增函数.
证明令r3=u,则C0(λc,act,α)可改写为
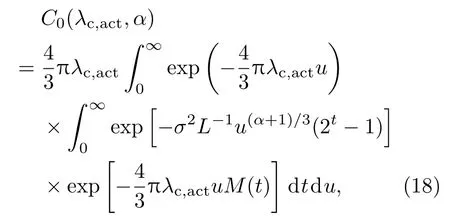
式中
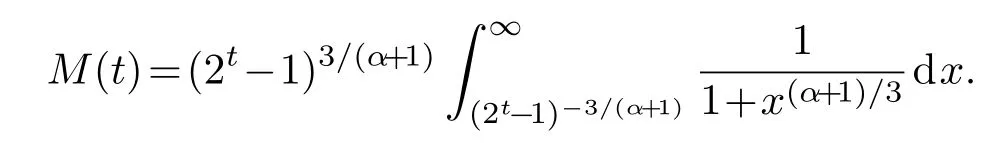
假设λc,act1<λc,act2,将λc,act2代入(18)式,则

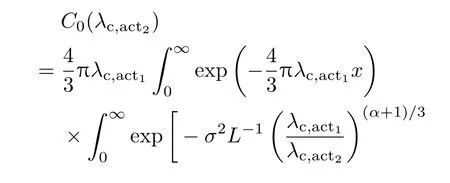


证毕.
在实际系统带宽和多用户连接场景下,下行信道容量为
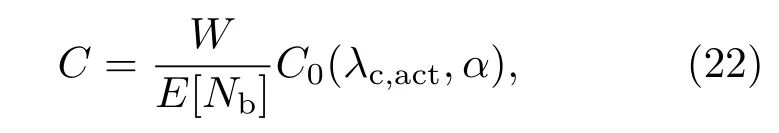
式中W表示系统带宽,E[Nb]以及C0(λc,act,α)分别由(5)式和(10)式确定.
4 能效优化
通过小基站休眠概率的最优化来实现整个小基站网络能耗最低的目标.优化问题表述如下:

其中,前两个约束条件分别是平均接入率和信道容量,Enet表示整个小基站网络的能量消耗,psl表示小基站休眠概率,Pact和Psl分别表示小基站处于工作状态和休眠状态下的发射功率[6],Pact>Psl.
由于Pact−Psl>0,不难发现Enet是关于psl的单调递减函数.因此,最优化问题P0可等效为

由于前两个约束之间没有耦合关系,我们可以对这两个约束条件分别求最优解.
1)满足平均接入率约束条件的解为psl,RAC≤其中由下式确定[6]:
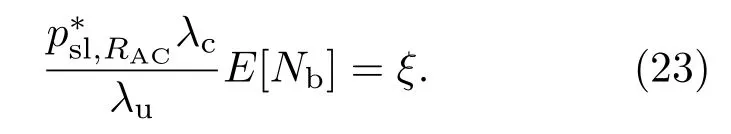
2)根据引理1、推论1以及休眠概率psl的数学定义psl=1−λc,act/λc,不难发现下行信道容量C是关于psl的单调递减函数.因此,满足传输信道容量约束条件的解为其中由下式确定:
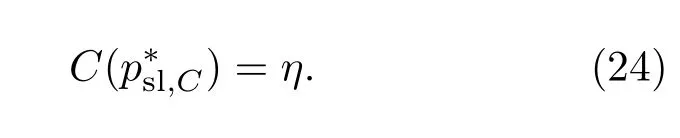
(23)式和(24)式的解均可通过经典二分搜索算法求得.
综合考虑两个约束条件,则最优休眠概率为

整个小基站网络的最低能耗为

5 仿真结果及分析
5.1 对C0和RAC的仿真与分析
考虑一个分布有大量小基站的城市中心球形区域,其半径R=100 m.小基站在此区域内随机分布,其空间坐标(x,y,z)满足x,y,z在[−R,R]间随机分布.小基站到目标用户(位于球心)的距离为处于工作状态的小基站密度λc,act在5×10−6—5×10−4m−3之间变化. 对于传统的2D模型,需将所有小基站投影到以R为半径的平面圆形区域,所有小基站到目标用户(位于圆心)的距离需重新计算.单位带宽下的信道容量C0和平均接入率RAC与λc,act的关系分别如图1和图2所示.

图1 不同环境下C0与λc,act的关系(α=4)Fig.1.Relationship between C0and λc,actin different environment(α=4).
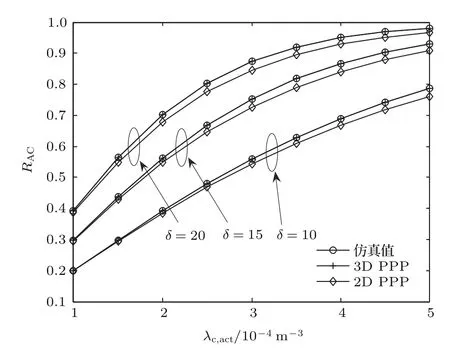
图2 不同基站接入数δ下RAC与λc,act的关系Fig.2.Relationship between RACand λc,actfor different values of base station connectionδ.
从图1和图2可以看出,基于3D PPP理论的信道容量和平均接入率值均接近实际环境下的仿真值并且优于传统的2D PPP模型.从图1还可以看出,无噪声环境下信道容量的理论值和仿真值均为一固定值(与基站密度无关),这与(17)式相符合.而在有噪声的环境下,信道容量随着处于工作状态的小基站密度λc,act的增大而增大并逐渐收敛到无噪声环境下的固定值.其原因在于,当λc,act足够大时,干扰远大于噪声而成为整个小基站网络中的主导(即噪声可以忽略不计),因而信道容量收敛到无噪声环境下的固定值.图2表明平均接入率随着λc,act和每个基站最大接入数δ的增大而增大.其原因在于,无论λc,act还是δ增大,都将导致整个网络中可用信道数增多,也就必然导致平均接入率的增大.除此之外,从图2还可以发现,平均接入率随着λc,act单调递增,这对下一步能效优化仿真时计算平均接入率约束条件下的最佳休眠概率带来极大的帮助.上述仿真结果表明在信道容量和平均接入率这两项网络性能方面,3D PPP模型均优于传统的2D模型,因此后续基于信道容量和平均接入率约束的能效优化仿真中不再比较本文的3D PPP模型与传统2D模型.
5.2 能效优化仿真与分析
考虑一个基于3D PPP模型的小基站蜂窝网络,除特别说明外,相关仿真参数如表1所示[21].

表1 仿真参数Table 1.Simulation parameters.
在实际系统带宽和多用户连接场景下,用户下行信道容量C与λc,act的关系如图3所示.

图3 不同基站接入数δ下信道容量C与λc,act的关系Fig.3.Relationship between channel capacity C and λc,actfor different values of base station connection δ.
从图3可以看出,下行信道容量C随着λc,act的增大而迅速增大.原因在于随着λc,act的增大,C0不断增加而E[Nb]不断减小,两者结合导致C快速增大.进一步分析可以发现,C随着λc,act的增大同样逐渐收敛到一固定值.原因在于当λc,act足够大时,C0→1.61且E[Nb]→1.除此之外,C随着δ的增大而减小,这是因为随着δ的减小,每个基站接入的用户数减少,每个用户分配到的系统带宽增大,下行信道容量也随之增大.
图4和图5分别为小基站的休眠概率psl与平均接入率约束门限和信道容量约束门限之间的关系.从图中可以看出,随着约束门限的提升,psl逐步降低(即较高的通信性能要求更多的基站进入工作状态来支撑).然而,从图4和图5可以发现,在平均接入率约束条件下,psl随着δ的增大而增大,而在信道容量约束条件下,psl随着δ的增大而减小.这是因为随着δ的增大,每个基站接入的用户会增多,少量基站进入工作状态即可满足平均接入率要求,因此psl增大.随着δ的增大,每个基站接入用户不断增多,每个用户分到的带宽变小,这导致信道容量的降低,因而需要更多的基站从休眠状态进入工作状态来满足信道容量的要求,因此psl减小.从图5还可以发现,当δ=20、信道容量约束门限为3.1 Mbit·s−1以上,δ=15、信道容量约束门限为3.2 Mbit·s−1以上,以及δ=10、信道容量约束门限为3.7 Mbit·s−1以上时,psl值降为0,这意味着即使所有基站都进入工作状态,也未必能满足这一信道容量的要求.

图4 不同基站接入数δ下休眠概率与平均接入率门限的关系Fig.4.Relationship between sleep probability and average connecting ratio threshold for different values of base station connection δ.
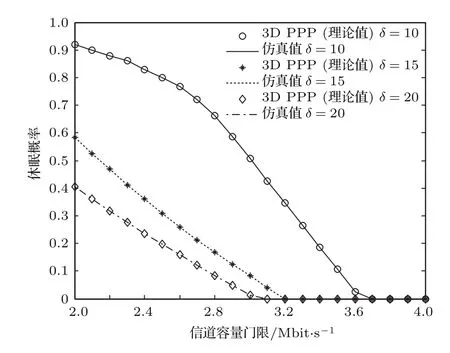
图5 不同基站接入数δ下休眠概率与信道容量门限的关系Fig.5.Relationship between sleep probability and channel capacity threshold for different values of base station connection δ.
图1—图5中的理论值是根据推导的公式直接计算得到的,而仿真值是根据小基站分布、路径损耗等仿真环境(表1)计算得到的.图1—图5中的仿真值和理论值基本一致,说明使用3D PPP模型描述小基站的分布是合理的,本文对信道容量以及平均接入率的推导也是正确的.
整个小基站网络的能耗Enet与基站最大接入用户数δ的关系如图6所示.从图6可以清楚地看出,合理选取δ值可以实现网络能耗的最小化.一方面,仅有平均接入率约束时,网络能耗随着δ的增大而减小,原因在于psl随着δ的增大而增大,而psl的增大直接导致Enet的降低.另一方面,仅有信道容量约束时,网络能耗随着δ的增大而增大,原因在于psl随着δ的增大而减小,而psl的减小直接导致Enet的增大.在这两个条件的共同约束下,δ∗=17成为最佳选择.如图6所示,在平均接入率门限为90%且下行信道容量门限为2.5 Mbit·s−1的条件下,当δ取最佳值17时,整个小基站网络的能耗将降低约21%(当δ∗=17时Enet=0.0289,而无基站休眠时Enet=0.0366).因此,通过基站休眠机理并结合接入参数的合理配置完全可以实现网络能耗的最小化.

图6 不同约束条件下网络能耗与基站最大用户连接数的关系Fig.6.Relationship between network energy and maximum connection for different constraints.
6 结 论
本文将3D PPP小基站模型应用于基于休眠机理的网络能效优化.在平均接入率和信道容量双重约束下,通过网络能耗最小化问题确定小基站的休眠概率.仿真结果表明在网络优化设计中,需要兼顾接入率和信道容量两方面的性能约束.更为重要的是,通过对基站最大用户连接数的合理配置并结合基站休眠,可以使网络能耗显著降低.
[1]Jo H,Mun C,Moon J,Yook J 2010IEEE Trans.Wireless Commun.8 2977
[2]Jo H,Sang Y,Xia P,Andrews J G 2012IEEE Trans.Wireless Commun.11 3484
[3]Soh Y S,Quek T Q S,Kountouris M,Shin H 2013IEEE J.Sel.Areas Commun.31 840
[4]Mugume E,So D K C,Alsusa E 2015IEEE Global Communications Conference,San Diego,December 6–10,2015 p1
[5]Ashraf L,Boccardi F,Ho L 2011IEEE Commun.Mag.49 72
[6]Mugume E,So D K C 2015IEEE International Conference on Communications,London,June 8–12,2015 p192
[7]Tsilimantos D,Gorce J M,Altman E 201332nd IEEE International Conference on Computer CommunicationsTurin,April 14–19,2013 p1097
[8]Qu D,Zhou Y,Tian L,Shi J 2016IEEE Global Communications Conference,Washington DC,December 4–8,2016 p1
[9]Cao D,Zhou S,Niu Z 2012IEEE International Conference on Communications,Ottawa,June 10–15,2012 p4379
[10]Cao D,Zhou S,Niu Z 2013IEEE Trans.Wireless Commun.12 4350
[11]Niu Z,Wu Y,Gong J 2010IEEE Commun.Mag.48 74
[12]Peng J,Hong P,Xue K 2014IEEE Commun.Lett.18 612
[13]Kim J,Jeon W S Jeong D G 2015IEEE Commun.Lett.19 641
[14]Dhillon H S,Ganti R K,Baccelli F,Andrews J G 2012IEEE J.Sel.Areas Commun.30 550
[15]Pan Z,Zhu Q 2015IEEE Commun.Lett.19 831
[16]Omri A,Hasna M O 2016IEEE International Conference on Communications,Kuala Lumpur,May 23–27,2016 p1
[17]Parkvall S,Furuskar A,Dahlman E 2011IEEE Commun.Mag.49 84
[18]Ferenc J,Neda Z 2007Physica A385 518
[19]Ge X,Tu S,Mao G,Wang C 2016IEEE Wireless Commun.23 72
[20]Andrews J G,Baccelli F,Ganti R K 2011IEEE Trans.Commun.59 3122
[21]Auer G 2011IEEE Wireless Commun.Mag.18 40
Energy efficiency optimization in three-dimensional small cell networks based on dormant strategy∗
Pan Zi-Yu1)2)†Hu Han2)Yang Jie1)
1)(Department of Communication Engineerings,Nanjing Institute of Technology,Nanjing 211167,China)
2)(Jiangsu Provincial Key Laboratory of Wireless Communications,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
25 April 2017;revised manuscript
9 August 2017)
Wireless cellular networks all over the world are undergoing a profound transformation evolving from voice-oriented to data networks.Larger coverage area,better service quality,and lower energy cost are the key issues in the deployment of cellular networks.To achieve these goals,small cells,such as the femtocells and picocells,have become an important part of the current 4G and future 5G wireless cellular networks.Generally speaking,small cell networks are deployed according to the peak traffic load,which causes energy waste during low traffic periods.Against this background,energy efficiency optimization has become one of the research hotspots in wireless communications.In this paper,we focus on the energy efficiency problem in small cell networks in which a large number of small cells are spatially deployed in dense urban areas such as office buildings and shopping malls.We optimize the energy efficiency through small cell dormant mechanism under the constraints of average connection ratio(ACR)and average downlink channel capacity.First,we derive the mathematical expressions for average downlink channel capacity and ACR in three-dimensional(3D)small cell networks by Poisson point process(PPP)theory.Second,the monotonicities of channel capacity and ACR are analyzed in detail.Then,based on the results of monotonicity analysis,the optimal small cell dormant probability is calculated to satisfy the constraints of ACR and average downlink channel capacity respectively.Finally,we formulate a network energy consumption minimization problem subject to the constraints of ACR and channel capacity to determine the dormant probability.In addition,we also formulate an optimal maximum connection number of small cells,which minimizes the energy consumption subject to the joint constraints of ACR and channel capacity.Numerical results show that our 3D PPP model is more accurate than the traditional two-dimensional(2D)one in both channel capacity and ACR performance,and that the energy consumption of small cell networks can be reduced by about 21%of the total energy consumption with the dormant strategy in this paper.More importantly,the optimal dormant probability and appropriate con figuration of the maximal number of connection can be effectively used to design small cell dormant strategy for 3D small cell networks.
small cell networks,energy efficiency,dormant strategy,Poisson point process
PACS:01.20.+x,92.60.Aa,02.60.CbDOI:10.7498/aps.66.230101
*Project supported by the Youth Foundation of Nanjing Institute of Technology,China(Grant No.QKJA201505),the Platform and Laboratory of Nanjing Institute of Technology,China(Grant No.PTKJ201603),the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.61401225),and the Young Scientists Fund of Natural Science Foundation of Jiangsu Province,China(Grant Nos.BK20140894,BK20160781).
†Corresponding author.E-mail:panziyu@njit.edu.cn
(2017年4月25日收到;2017年8月9日收到修改稿)
小基站通常部署在写字楼、商贸区等城市密集区域以弥补传统宏基站在覆盖和传输方面的不足.小基站的分布一般是根据高峰时的网络负荷设计的,这必然导致网络负荷较低时的资源浪费.讨论了在平均接入率和信道容量双重约束下基于休眠机理的三维小基站蜂窝网络的能效优化问题.借助泊松点过程理论推导了三维小基站网络下行信道容量和平均接入率的数学表达式.通过分析下行信道容量和平均接入率的单调性得出同时满足传输信道容量和接入率要求的最佳休眠概率.分析了小基站最大用户连接数的最佳值,通过对该参数的合理配置,可以在满足通信指标的前提下最大程度地降低网络能耗.仿真结果表明,设计的基站休眠机理可以使小基站网络的能耗下降约21%.
10.7498/aps.66.230101
∗南京工程学院青年基金(批准号:QKJA201505)、南京工程学院平台及实验室专项(批准号:PTKJ201603)、国家自然科学基金青年科学基金(批准号:61401225)和江苏省自然科学基金青年基金(批准号:BK20140894,BK20160781)资助的课题.
†通信作者.E-mail:panziyu@njit.edu.cn

