一种生成质量最优路径纠缠微波信号的压缩参量选择方法∗

王湘林 吴德伟 李响 朱浩男 陈坤 方冠

(空军工程大学信息与导航学院,西安 710077)

一种生成质量最优路径纠缠微波信号的压缩参量选择方法∗

王湘林 吴德伟†李响 朱浩男 陈坤 方冠

(空军工程大学信息与导航学院,西安 710077)

路径纠缠微波,信号质量,压缩参量,纠缠微波光子总数期望值

1 引 言

随着微观领域研究的不断推进,研究者们欣喜地发现利用微观粒子的量子纠缠特性能够打破经典理论对信息技术的限制[1,2],这很好地迎合了当今信息时代不断膨胀的信息需求.科学研究与实际需求的契合极大地促进了微观粒子量子纠缠特性的研究成为科研前沿,从电子纠缠到光子纠缠、再到微波光子纠缠,量子纠缠特性不断以各种形式呈现出来[3−7].

随着光学频段量子理论逐步成熟,光学频段纠缠的实际应用也日渐广泛[8].目前,已有涉及量子通信、雷达等领域的应用的报道[9,10].例如,我国于2016年8月16日凌晨1时45分成功发射了“墨子”号卫星,它是全球首颗量子科学实验卫星[11],“京沪干线”大尺度光纤量子通信骨干网即将竣工,这些充分说明中国在量子信息研究行列已经走在了世界前列.但是就量子纠缠信号的应用前景而言,微波频段信号更适于自由空间传播,且具有更远的有效传播距离及更强的抗干扰能力等优势,决定了纠缠微波信号能够更好地发挥量子纠缠的作用.

受自身极低能量、探测手段等因素的限制[12],对纠缠微波的应用不能像纠缠光子那样,直接利用单个纠缠光子来进行信息的传递,而需要实现微波场的纠缠,进而以纠缠微波场信号作为信息载体,才能实现对信息的处理、传递[13]等.这样一来,生成空间上分离的纠缠微波信号就成了实现如爱因斯坦所言“远距离鬼魅般相互作用”的必要条件[2],而路径纠缠微波信号很好地满足了这些条件:一方面,路径纠缠微波作为微波频段的纠缠信号,它比光学频段的纠缠信号更适于自由空间传播,且传播距离远超光学信号;另一方面,两路路径纠缠微波信号能够保持纠缠状态沿着空间上分离的路径传播[14,15],路径纠缠微波的这种契合使量子纠缠微波领域成为又一个被竞相争夺的科研高地[16].

目前,国内外对于纠缠微波的研究尚不深入.一方面,对路径纠缠微波信号仍缺乏相对完善的质量评价方法;另一方面,现有路径纠缠微波信号制备方案所生成信号的纠缠度极低,导致对纠缠微波的实验研究难度极大.基于以上两个方面的问题,本文提出了一种信号质量评价方法,进而基于这种质量评价方法提出一种生成质量最优路径纠缠微波信号的压缩参量选择方法.

2 路径纠缠微波及其生成原理

2.1 路径纠缠微波

路径纠缠微波是微波频段量子纠缠的体现.光子的能量比微波光子的能量要大得多,相应地,光学频段信号所体现出来的粒子性较强,而微波频段信号体现出来的波动性较强,这就造成了光学频段量子纠缠特性与微波频段量子纠缠特性在研究和实际应用中信号表现形式上的差异.目前,光学频段量子纠缠特性的研究和应用主要集中于单个纠缠光子对,而对于微波频段量子纠缠特性的研究和应用则因受到微波光子自身低能量的限制,需要从纠缠微波场信号的角度出发.本文中所研究的路径纠缠微波信号就是微波场信号的形式.路径纠缠微波信号是指分布在空间上处于分离状态的两个传播路径上,且能够保持纠缠状态沿着各自的路径传播到信息系统的任意两个部件的纠缠微波场信号[7].

2.2 路径纠缠微波生成原理

制备路径纠缠微波过程中,最为关键的元器件是微波分束器[17].常见的微波分束器有超导180°混合环、威尔金森功分器,基于约瑟夫森结的约瑟夫森混合器实质上也是一种微波分束器[17−19].

以超导180°混合环用作微波分束器为例,如图1所示,由约瑟夫森参量放大器(JPA)产生的压缩态信号[20]和50Ω负载产生的热态作为超导180°混合环的两路输入信号,分别从端口A和C进入混合环,在其内部的超导环中形成干涉效应[18].通过适当设计超导180°混合环内部超导环的周长,使两路输入信号在端口A和C处产生相消干涉,而端口B和D处产生相长干涉,进而在两个输出端口得到两路路径纠缠微波信号[17]:

其中,in(out)表示该物理量为超导180°混合环输入信号(输出信号)的物理量,1(2)表示该物理量为超导180°混合环输入或输出的两个不同端口处信号的物理量,B为信号带宽,R0为50Ω本地负载,h为普朗克常量,f为信号频率,为产生算符,a1,a2为湮灭算符.

由上述可见,微波分束器的作用实质上就是充当路径纠缠器.

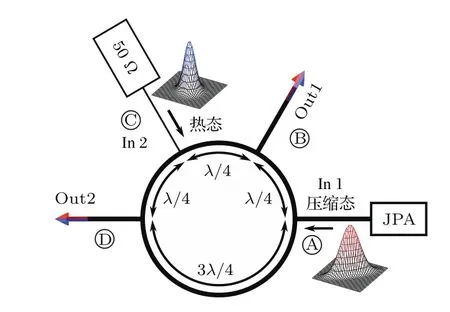
图1 (网刊彩色)超导180°混合环产生路径纠缠微波示意图Fig.1.(color online)Schematic diagram of using superconducting 180°hybrid ring to generate path entangled microwave.

3 路径纠缠微波信号的算符表示及其质量的影响因素分析

在理想情况下,分别使用真空态和压缩态作为超导180°混合环的两路输入信号,真空态和压缩态在超导环中产生干涉效应的过程中,真空态与压缩态发生相互作用,相当于压缩算符作用于真空态,产生双模压缩真空态.在实际实验中无法产生理想情况下的真空态,但可以通过控制负载阻值的大小产生接近真空态的热态来近似代替真空态.因此,可以用双模压缩真空态近似描述超导180°混合环产生的路径纠缠微波信号[21].

将双模压缩真空态用双模光子数态|m〉a1out|n〉a2out展开有:

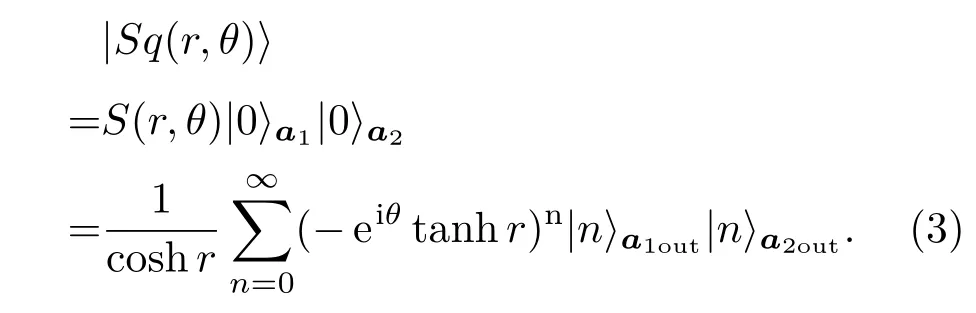
令

则

生成2n微波光子纠缠的概率为P2n=|Cn,n|2.(5)式中只包含微波光子数相同的项,且它们出现的概率相等,这表明它们之间存在着强关联特性.由此可以看出,超导180°混合环生成的纠缠微波以相同的概率P2n在空间上分离的两个路径上各产生n个微波光子,并且它们处于量子纠缠状态,两路输出信号在宏观上表现为路径纠缠信号.由(4)式可以看出,不同微波光子数纠缠产生的概率,不但与压缩幅r,压缩角θ有关,而且还与单路纠缠微波光子数n有关.根据归一化条件,有也就是说,当生成某一数量的纠缠微波光子的概率变化时,必然影响到生成其他数量的纠缠微波光子的概率.因此,可以初步推断影响路径纠缠微波生成质量的因素有压缩幅和压缩角(微波光子数量不可控,因此不予考虑).

4 一种路径纠缠微波信号生成质量评价方法

对于纠缠信号而言,只有处于纠缠状态的粒子才能被用作信息传递的媒介,而处于其他状态的粒子对信息传递来说毫无用处,也就相当于经典信号中的噪声.因此,一般从信号纠缠度的角度来评价纠缠信号的质量,纠缠度是指纠缠信号中纠缠粒子数占粒子总数的比例[22,23].

一方面,从上述路径纠缠微波的生成原理可以看出,输入约瑟夫森参量放大器的微波信号中包含的微波光子数量巨大且不可控,因此合理假设每次输入的微波光子数是近似相等的;另一方面,可以通过纠缠微波光子总数的期望值E(N)来表示所产生信号中包含的纠缠微波光子的数量.那么,通过E(N)就可以近似表征路径纠缠微波信号的纠缠度,从而实现对路径纠缠微波信号质量进行评价:纠缠微波光子总数的期望值越大,说明纠缠信号的纠缠度越高,信号质量越好.

纠缠微波光子总数期望值的表达式为

5 通过控制压缩幅来生成质量最优路径纠缠微波信号

从(6)式可以看出,E(N)的值只与压缩幅有关,而与压缩角无关.那么,可以通过改变r值对所生成信号的纠缠微波光子数的期望值E(N)进行控制,使所得到的路径纠缠微波信号的纠缠度尽可能大.通过仿真,取不同压缩幅值r,得到2n个微波光子纠缠及对应概率,如图2所示.

图2 (网刊彩色)压缩幅值与纠缠微波光子数及对应概率的变化规律Fig.2.(color online)Change rule of generating different number of microwave photons entanglement and corresponding probability when the value of squeezed parameter changes.

生成2n微波光子纠缠的概率随着n值增大迅速减少,最终趋近于0;因此,可以通过仿真给出单路纠缠微波光子数n的有效值,进而进行纠缠微波光子总数期望值E(N)的近似计算.从理论上来讲,压缩幅值越大所产生的路径纠缠微波信号的纠缠度越高,当压缩幅值趋向无穷大时,信号纠缠度为1,此时,产生的两路信号是完全纠缠的,但器件要达到这样的性能,工程上是无法实现的.在实际中,一般将压缩幅r的最大值取为3[24].在本文确定n有效值的仿真实验中,将r值分别取0.5,1.0,1.5,2.0,2.5,3.0.如图3所示,仿真实验结果表明,在压缩幅取不同值的情况下,当n取13时,相应数量的纠缠微波光子出现的概率均接近或远小于千分之一.结合当前工程上产生多个微波光子纠缠的能力有限的现状,本文将单路纠缠微波光子数n的有效值取为[1,13](n∈Z+),即纠缠微波光子数2n的最大有效值为26.

在确定了单路纠缠微波光子数n有效值的情况下,要得到E(N)值,还必须确定r的值.本文提出一种使路径纠缠微波信号纠缠度最大的r值确定方法:通过取各个有效n值处,产生2n个微波光子纠缠概率最大时的r值构成一组压缩幅值,分别计算对应的E(N).这样,可以得到一组E(N)值,在这些E(N)值中必然会有最大值,而这个最大值E(N)max所对应的r值就是我们所要寻找的能产生质量最优的路径纠缠微波信号的压缩幅值.

图3 压缩幅r取不同值时产生2n个微波光子纠缠的概率变化趋势Fig.3.Tendency of the probability of generating different number of microwave photons entanglement when the value of squeezed parameter changes.

图4 (网刊彩色)(a)在压缩幅取不同值时产生2n个微波光子纠缠的概率分布情况;(b)各个微波光子数纠缠概率最大时所对应的压缩幅值Fig.4.(color online)(a)Distribution of the probability of generating different number of microwave photons entanglement,when the value of squeezed parameter changes;(b)squeezed parameter corresponding to the maximum probability of generating each number of microwave photons entanglement.

图4(b)为图4(a)中产生不同微波光子数纠缠的最大概率处压缩幅值点的连线.从图4(b)中可以清楚地看到,通过仿真得到产生2n(n∈[1,13],n∈Z+)个微波光子纠缠概率最大时的一组r值,依次为:0.89,1.15,1.32,1.44,1.55,1.63,1.70,1.77,1.82,1.87,1.92,1.95,1.99.

6 仿真实验结果分析

控制压缩幅r分别取上述值时,在单路有效纠缠微波光子数n∈[1,13](n∈Z+)的情况下,通过仿真得到一组E(N)值如图5所示,上述的一组r值所对应的纠缠微波光子总数的期望值E(N)依次为:1.02,1.96,2.71,3.20,3.53,3.69,3.76,3.77,3.74,3.68,3.60,3.54,3.44.从图5中还可以看出,当压缩幅小于1.77时,增大压缩幅值使生成信号的纠缠微波光子总数的期望值相应地增大,从各点连线的斜率可以看出,其增大的幅度先增加,后减少,在压缩幅值为1.15左右,E(N)的增加幅度最大;当压缩幅大于1.77时,对应生成信号的纠缠微波光子总数的期望值反而逐渐减少,只是减少的幅度相对不大,且近似呈线性减少;在压缩幅取1.77时,对应生成信号的纠缠微波光子总数的期望值E(N)最大,最大值为3.77(图5中红色点位置).此时,产生的路径纠缠微波信号中纠缠微波光子所占的比例最大,即信号的纠缠度最大,所产生信号的质量最优.

图5 (网刊彩色)压缩幅分别取2n个微波光子纠缠概率最大时的r值,对应得到的纠缠微波光子总数的期望值Fig.5.(color online)The expectation of the number of entangled microwave photons when the squeezed parameter is assigned the value r,which is corresponding to the maximum probability of generating each number of microwave photons entanglement respectively.

仿真实验结果中出现这种以纠缠微波光子总数的期望值表征的纠缠度随压缩幅r值的增大先增加后减少的情况,其原因在于人为地将单路纠缠微波光子数n的有效值的最大值设定为13,而从理论上来讲,n是一个可以趋向于无穷大的量.由图3可以看出,人为设定n的有效值的最大值为13后,相对来说,当压缩幅取值较小时,生成小数量微波光子纠缠的概率很大,故此时小数量微波光子纠缠对纠缠微波光子总数的期望值的贡献较大,而当压缩幅的取值逐渐增大,不同数量微波光子纠缠产生的概率逐渐趋于一致,大数量微波光子纠缠对纠缠微波光子总数的期望值的贡献逐渐开始占据主导地位,但由于对单路纠缠微波光子n的有效值范围进行了设定,使得大数量微波光子纠缠对纠缠微波光子总数的期望值的贡献受到了限制.因此,仿真实验结果中出现了压缩幅值使小数量微波光子纠缠和大数量微波光子纠缠均相对贡献较大时,所得到的纠缠微波光子总数的期望值最大的情况.

7 总结与展望

以超导180°混合环作为微波分束器的路径纠缠微波信号生成方案为例,分析了路径纠缠微波信号的生成原理,继而基于一种间接的纠缠微波信号质量评价方法,提出了一种生成质量最优路径纠缠微波信号的压缩参量选择方法.通过仿真实验结果可以看出,当压缩幅值取1.77时,所生成的路径纠缠微波信号的质量最优,这也验证了该压缩参量选择方法是有效的.随着纠缠微波理论研究和技术的发展进步,未来在实验条件允许的情况下,可以通过实验对本文所提出的压缩参量选择方法进行验证.需要指出的是,本文中所提出的压缩参量选择方法是针对目前生成多个微波光子纠缠的能力有限的前提下,通过合理设定一个单路纠缠微波光子数n的有效值范围,进而确定该有效值范围内产生质量最优路径纠缠微波信号所对应的压缩幅值.这种方法提供的是一种压缩幅值选择思路,随着多个微波光子纠缠生成能力的提高,可以通过对单路纠缠微波光子数n的有效取值范围相应地进行调整,使所选择出来的最优压缩幅值始终与纠缠微波光子的生成能力保持同步.n取值范围的变化会引起纠缠微波光子总数的期望值发生变化,当单路纠缠微波光子数n的取值趋向于无穷大时,纠缠微波光子总数的期望值所表征的纠缠度会随着压缩幅值的增加而增大,并最终逐渐趋近于“1”,然而,在实际应用中要使单路纠缠微波光子数n的取值趋向于无穷大是缺乏可行性的.因此,提出在人为设定单路纠缠微波光子数n的有效值范围的前提下,通过对纠缠微波光子总数的期望值的比较来选择压缩幅值的办法,希望在实际的应用中能够在压缩参量的选择上为产生纠缠度尽可能大的路径纠缠微波信号提供参考.另外,通过仿真结果可以看出,本文在单路纠缠微波光子数n有效值取到13的情况下,纠缠微波光子总数的期望值在数值上非常接近,这说明在单路纠缠微波光子数n有效值的选择上,细微的偏差都有可能造成所选择的压缩幅值偏离最优的压缩幅值.尽管如此,文中所提出的压缩参量选择方法,为纠缠微波这一新兴领域的实验研究、实际应用提供了一种控制所生成路径纠缠微波信号质量的思路.

[1]Braunstein S L,van Loock P 2005Rev.Mod.Phys.77 513

[2]Horodecki R,Horodecki P,Horodecki M,Horodecki K 2009Rev.Mod.Phys.81 865

[3]Herrmann L G,Portier F,Roche P,Yeyati A L,Kontos T,Strunk C 2010Phys.Rev.Lett.104 026801

[4]Recher P,Sukhorakov E V,Loss D 2001Phys.Rev.B63 165314

[5]Ou Z Y,Pereira S F,Kimble H J,Peng K C 1992Phys.Rev.Lett.68 3663

[6]Raimond J M,Brune M,Haroche S 2001Rev.Mod.Phys.73 565

[7]Johansson G 2012Physics5 120

[8]Arndt M,Hornberger K,Zeilinger A 2005Phys.World18 35

[9]Gisin N,Thew R 2006Nat.Photon.1 165

[10]Zhou C H,Qian W P 2015Radar Sci.Tech.13 457(in Chinese)[周城宏,钱卫平2015雷达科学与技术13 457]

[11]Peng C Z,Pan J W 2016BCAS31 1096(in Chinese)[彭承志,潘建伟2016中国科学院院刊31 1096]

[12]Menzel E P,Di Candia R,Deppe F,Eder P,Zhong L,Ihmig M,Haeberlein M,Baust A,Hoffmann E,Ballester D,Inomata K,Yamamoto T,Nakamura Y,Solano E,Marx A,Gross R 2012Phys.Rev.Lett.109 250502

[13]Di Candia R,Menzel E P,Zhong L,Deppe F,Marx A,Gross R,Solano E 2014New J.Phys.16 015001

[14]Menzel E P 2013Ph.D.Dissertation(Munich:Technic University of Munich)

[15]Eder P 2012Ph.D.Dissertation(Munich:Technic University of Munich)

[16]Nakamura Y,Yamamoto T 2013IEEE Photon.J.5 0701406

[17]Mariantoni M,Menzel E P,Deppe F,Araque Caballero M A,Baust A,Niemczyk T,Hoffmann E,Solano E,Marx A,Gross R 2010Phys.Rev.Lett.105 133601

[18]Hoffmann E,Deppe F,Niemczyk T,Wirth T,Menzel E P 2010Appl.Phys.Lett.97 222508

[19]Bergeal N,Vijay R,Manucharyan V E,Siddiqi I,Schoelkopf R J,Girvin S M,Devoret M H 2010Nat.Phys.6 296

[20]Kim M S,Son W,Buzek V,Knight P L 2002Phys.Rev.A65 032323

[21]Li X,Wu D W,Wang X,Miao Q,Chen K,Yang C Y 2016Acta Phys.Sin.65 114204(in Chinese)[李响, 吴德伟,王希,苗强,陈坤,杨春燕2016物理学报65 114204]

[22]Vedral V,Plenio M B,Rippin M A,Knight P K 1997Phy.Rev.Lett.78 2275

[23]Shimony A 1995Ann.NY Acad.Sci.755 675

[24]Gerry G,Knight P 2005Introductory Quantum Optics(Cambridge:Cambridge University Press)p187

An approach to selecting the optimal squeezed parameter for generating path entangled microwave signal∗

Wang Xiang-Lin Wu De-Wei†Li Xiang Zhu Hao-Nan Chen Kun Fang Guan

(Information and Navigation College,Air Force Engineering University,Xi’an 710077,China)

2 May 2017;revised manuscript

15 July 2017)

Quantum information theory can improve the performances of the classical information techniques by utilizing the entangled state of electromagnetic field.Path entangled microwave signal distributes its entangled states between spatially separated subsystems of an information system,which can be widely applied to quantum information technology in the future.Currently,there are only several reports on path entangled microwave signal generation.Therefore,the quality of path entangled microwave signal is far from satisfactory.In order to improve the quality of path entangled microwave signal further,we make a discussion about the factors that affect the quality of it and design a quality evaluation scheme for it.Based on the designed quality evaluation scheme,an optimal squeezed parameter selection method is suggested.

Firstly,the generation principle of path entangled microwave signal is brie fly introduced,and the generated signal is denoted as quantum mechanics operator in the Fock state representation.In the meantime,the qualitative relationship between generated signal and the squeezed parameter is determined.Secondly,a quality evaluation method for path entangled microwave signal is proposed:the quality of generated signal is evaluated by comparing with the expectation value of the entangled microwave photon number which re flects the degree of quantum entanglement.Finally,an approach to selecting the optimal squeezed parameter for generating the path entangled microwave signals is proposed based on the quality evaluation method.The process of it is as follows:an array of squeezed parameters which achieve the highest entanglement probability of different microwave photons is acquired under the premise that the maximal effective number of entangled microwave photons is set to be a certain value.Then an array of expectation values of number of entangled microwave photons corresponding to these squeeze parameters is acquired,and the squeezed parameter corresponding to the largest expectation value is what we are searching for.Through theoretical analysis,we draw a conclusion that the quality of path entangled microwave signal is determined by squeezed parameter.Accurately,it is related to the squeezed degree,but unrelated to the squeezed angle.From simulations,we find that the maximal expectation value of the total number of entangled microwave photons is 3.77 when the simulation proceeds on condition that the maximal number of effective entangled microwave photons is set to be 26.And its corresponding squeezed degree value is 1.77,which means that the optimal path entangled microwave signal can be generated when we set the value of squeezed degree to be 1.77.And our method is proved effective by the simulation results.We provide an original idea on generating high-quality path entangled microwave signals for its experiments and applications.

path entangled microwave,quality of signal,squeezed parameter,expectation of the number of entangled microwave photons

PACS:03.67.–a,03.67.Bg,03.65.Ud,84.90.+aDOI:10.7498/aps.66.230302

*Project supported by the National Natural Science Foundation of China(Grant No.61573372).

†Corresponding author.E-mail:wudewei74609@126.com

(2017年5月2日收到;2017年7月15日收到修改稿)

介绍了路径纠缠微波及其生成原理,将生成信号以量子力学算符的形式表示,并在光子数态表象下展开,定性地给出了生成信号与压缩参量之间的关系.提出了一种路径纠缠微波信号质量评价方法,即通过信号中纠缠微波光子总数的期望值表征信号的纠缠度,间接实现对信号质量的评价.基于这种信号质量评价方法,提出了一种生成质量最优路径纠缠微波信号的压缩参量选取方法:在近似确定有效纠缠微波光子数的前提下,找出生成不同微波光子数纠缠概率最大时的一组压缩参量值,进而得出各个压缩参量值所对应的一组纠缠微波光子总数的期望值,其中的最大值对应的压缩参量值即为生成质量最优信号所要选择的压缩参量值.通过理论分析,发现路径纠缠微波信号质量由压缩参量决定,且只与压缩幅有关,而与压缩角无关.仿真实验结果表明,在纠缠微波光子数的最大有效值取为“26”时,纠缠微波光子总数期望值的最大值对应的压缩幅值为1.77,即压缩幅取此值时所得到的路径纠缠微波信号质量最佳,仿真结果表明该方法是有效的.本文的研究为路径纠缠微波在实验研究和实际应用中如何生成高质量信号的问题提供了思路.

10.7498/aps.66.230302

∗国家自然科学基金(批准号:61573372)资助的课题.

†通信作者.E-mail:wudewei74609@126.com