具有三角自旋环的伊辛-海森伯链的热纠缠∗

郑一丹 毛竹 周斌

(湖北大学物理与电子科学学院,武汉 430062)

具有三角自旋环的伊辛-海森伯链的热纠缠∗

郑一丹 毛竹†周斌‡

(湖北大学物理与电子科学学院,武汉 430062)

热纠缠,配对纠缠度,伊辛-海森伯链,转移矩阵方法

1 引 言

含有几何阻挫的自旋系统在零温和有限温度下,由量子涨落和热效应引起的相变,因其表现出有趣的新相位和丰富的基态以及热力学性质而备受关注[1−6].最简单的几何阻挫模型是自旋粒子间具有反铁磁相互作用的三角排列团簇,典型代表是单分子磁体Na9[Cu3Na3(H2O)9(α-AsW9O33)2]·26H2O(简称为{Cu3}) 等腰三角形{Cu3}模型[7,8].另外,具有三角自旋环的晶格自旋系统是磁性材料普遍含有的结构,也为研究几何阻挫系统提供了标准的理论模型.其中典型的具有三角自旋环的晶格自旋系统有角共享的三角形链(也称锯齿链或Δ链)的一维几何阻挫系统[9−13],以及三角反铁磁[14]和kagome晶格反铁磁系统的二维几何阻挫系统[15−17].

Mambrini等[18]研究了由自旋 1/2的海森伯粒子组成的三角自旋环相互交替形成的海森伯自旋链模型.研究结果表明,该模型每个自旋的基态剩余熵等于(1/4)ln2,四面体的耦合作用小于三角自旋环中的耦合作用时则存在单态和三重态能隙[18].之后,具有三角自旋环的海森伯链模型的研究引起人们的关注[19,20].如Rojas和Alcaraz[20]采用数值方法讨论了具有三角自旋环的海森伯链模型的相变及几何阻挫.在这类海森伯自旋团簇链中，由于自旋团簇之间为海森伯相互作用,这为严格求解带来较大的困难.人们在研究中发现,对于海森伯自旋团簇链模型中自旋团簇之间的海森伯相互作用较弱时,团簇之间的耦合自旋用经典的伊辛自旋取代海森伯自旋,得到的物理性质在定性上甚至在定量上与原海森伯自旋团簇链的数值和实验结果是一致的,而且转换后的伊辛-海森伯混合自旋系统通过转移矩阵方法[21−23],可以严格解析得到系统配分函数和热力学函数[24−27].Antonosyan等[28]研究了具有XXZ海森伯相互作用三角自旋环的伊辛-海森伯链模型,他们采用转移矩阵方法得到模型的热力学函数解析解,以及基态相图和系统的热力学以及磁学性质.Ohanyan[29]研究了具有自旋S=1/2的XXZ海森伯相互作用三角环的伊辛-海森伯链的相变.

外界温度对系统影响的热纠缠性质是量子信息技术的重要研究课题之一.自从Arnesen等[30]研究了海森伯自旋模型中的热纠缠性质后,人们对不同海森伯自旋体系中的热纠缠性质已经进行了大量的理论研究[31−48].最近,伊辛-海森伯自旋菱形链热纠缠的研究也取得了一定的进展[21,22,49−52]，但具有三角自旋环的伊辛-海森伯链的热纠缠性质尚未被讨论.本文研究具有三角自旋环的伊辛-海森伯链在磁场作用下的热纠缠性质.采用转移矩阵方法,数值计算具有三角自旋环的伊辛-海森伯链的配对纠缠度.分别讨论三角自旋环中自旋1/2粒子间具有XXX,XXZ和XY Z海森伯相互作用时,外加磁场和温度对三角自旋环中两个量子比特间配对热纠缠性质的影响.

2 理论模型和转移矩阵方法

2.1 理论模型

考虑在外加磁场作用下具有三角自旋环的伊辛-海森伯链系统.该模型是由海森伯自旋组成的三角环与伊辛自旋相互交替形成的无限长链,模型结构如图1所示,其中第i个团簇是由三个自旋S=1/2的海森伯自旋(Si1,Si2,Si3)和两个伊辛自旋(µi,µi+1)组成.具有三角自旋环的伊辛-海森伯链的哈密顿量H可表示为以下形式：

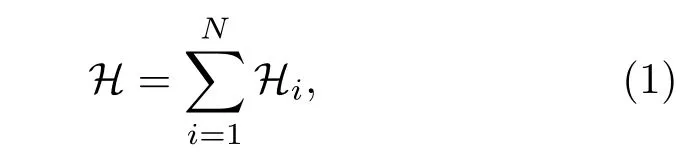
其中,Hi是第i个团簇的哈密顿量,可表示为以下形式：

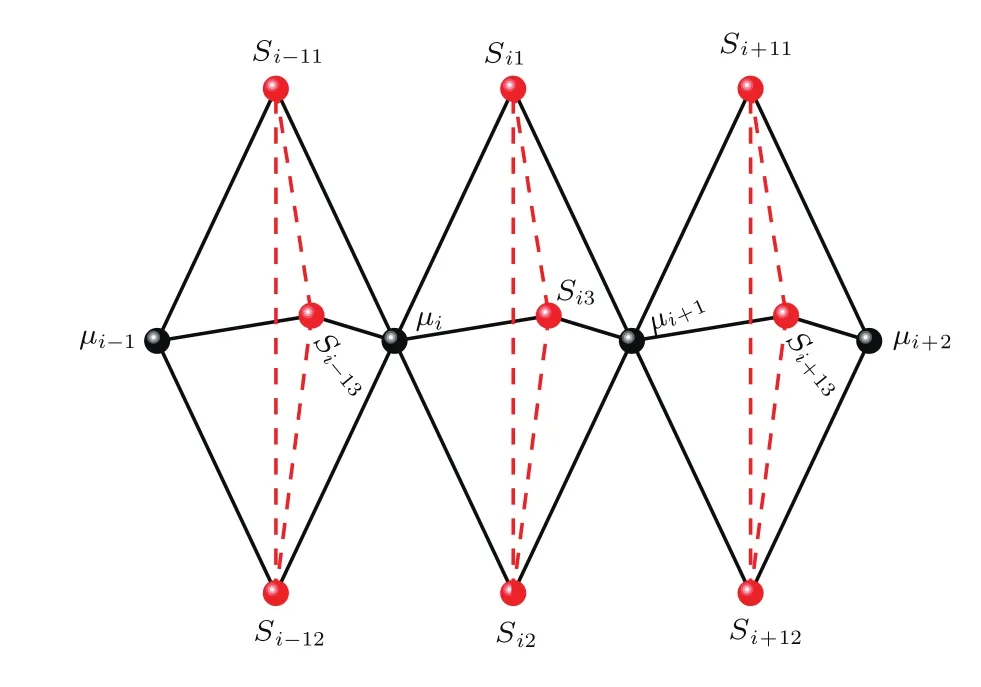
图1 (网刊彩色)海森伯自旋组成的三角自旋环与伊辛自旋相互交替形成的伊辛-海森伯链示意图 (图中红色球代表海森伯自旋粒子,黑色球代表伊辛自旋粒子)Fig.1.(color online)Schematic of Ising-Heisenberg chain with triangular plaquettes alternating with Ising spins(red balls represent Heisenberg spins,and black balls indicate Ising spins).

2.2 转移矩阵方法

利用转移矩阵方法计算该系统配分函数和约化密度矩阵.需要注意的是,系统第i和j个团簇哈密顿量是相互对易的,即[Hi,Hj]=0(i/=j).这种团簇间哈密顿量对易关系是该系统的配分函数进行部分因式分解的条件.系统配分函数ZN可表达为以下形式:

其中V(µi,µi+1)是含有伊辛自旋µi和µi+1的三量子比特算符,其定义式为[21]

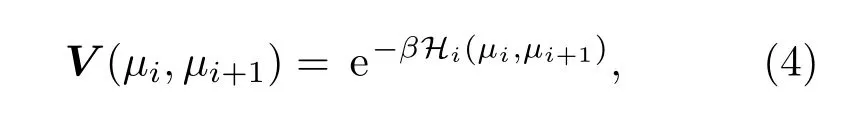
式中,β=(kBT)−1,kB是玻尔兹曼常数(为了计算简便,令kB=1).Tri是对第i个团簇的三量子比特算符V求迹,是对所有伊辛自旋态求和.通过对角化第i个团簇的哈密顿量Hi,可得到以下含有伊辛自旋的本征值:

其中，

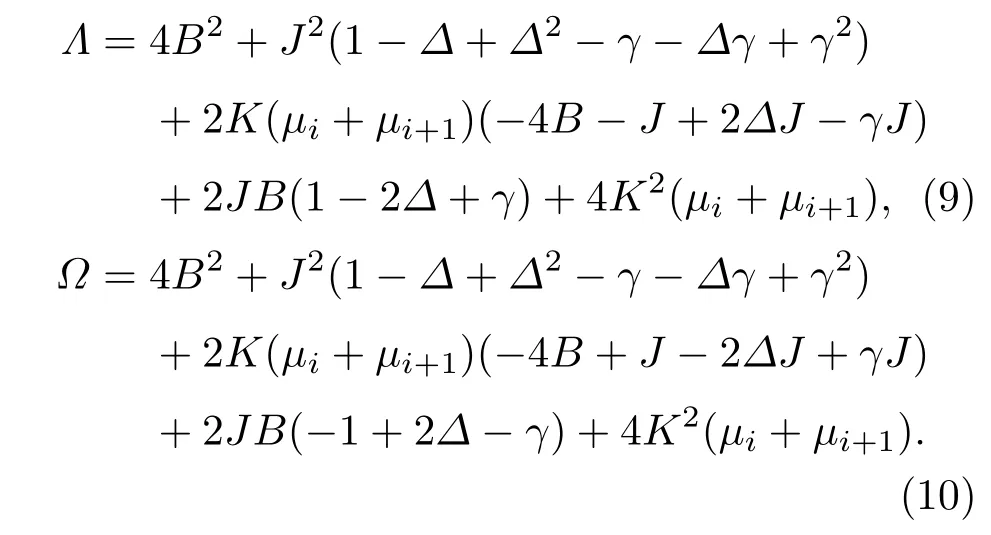
根据上述本征值以及对三量子比特算符V求迹,可得到玻尔兹曼因子w:

采用转移矩阵方法以及周期性边界条件,配分函数表达式(3)可改写为以下形式:

式中,W为转移矩阵,具体形式如下:

其中±1/2表示两个伊辛自旋态µi=±1/2.由(12)式可知,通过计算上述转移矩阵(13)式的本征值,可得该模型的配分函数:

式中,λ1,λ2是转移矩阵(13)式的本征值,且按降序排列,即λ1＞ λ2.考虑热力学极限(N→ ∞),配分函数将得到更简单的表达式：

采用转移矩阵方法将三角自旋环密度矩阵ρ的矩阵元表示为如下形式:

这里的三角自旋环密度矩阵ρ是8×8的矩阵,其矩阵元记为ρm,n,下标(m,n)标注密度矩阵元所在的行和列的序号(m,n=1···8).(16)式中的Rm,n为如下形式:

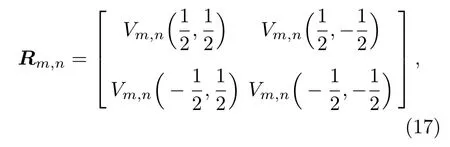
式中,Vm,n是矩阵V中第m行第n列中的矩阵元.令使转移矩阵W对角化的非奇异矩阵为U,则密度矩阵元(16)式可表示为如下形式:

考虑热力学极限,(18)式可以简化为

为了研究具有三角自旋环的伊辛-海森伯链在外加磁场作用下的热纠缠性质,将计算第i个团簇三角自旋环中量子比特Si1和Si2间的配对纠缠度C12,其定义为[53−55]

其中ζn(n=1,2,3,4)是算子

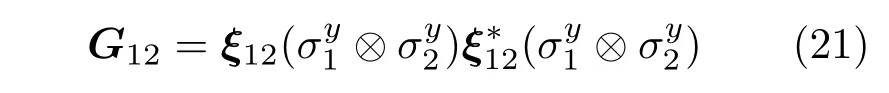
本征值的平方根,满足ζ1≥ζ2≥ζ3≥ζ4.是量子比特Si1(2)的泡利算符.(21)式中的ξ12是第i个团簇中量子比特Si1和Si2构成子系统的约化密度矩阵,该约化密度矩阵ξ12和算子G12是4×4的矩阵,下标(1,2)标注该子系统中量子比特的序号.是ξ12的复共轭矩阵.配对纠缠度C12的取值从0到1,C12=0为无纠缠存在,而C12=1表示系统处于最大纠缠,0＜C12＜1为部分纠缠.

3 结果与讨论

基于上述的转移矩阵方法,采用数值计算求解具有三角自旋环的伊辛-海森伯链的配对纠缠度C12,分别讨论三角自旋环中自旋1/2粒子间具有XXX,XXZ和XY Z海森伯相互作用时外加磁场以及温度对该系统热纠缠的影响.

3.1 XXX-海森伯模型

图2 (网刊彩色)配对纠缠度C12随磁场强度B和温度T的变化 (a)不同温度下,配对纠缠度C12随磁场强度B的变化;(b)临界温度Tc随磁场强度B的变化Fig.2.(color online)The concurrence of Ising-Heisenberg chain with triangular plaquettes versus the magnetic field and temperature:(a)The concurrence C12versus the magnitude of magnetic field B for the different temperatures;(b)the critical temperature Tcversus the magnitude of magnetic field B.

首先,考虑海森伯相互作用为各向同性的情况,令J=γ=Δ=K=1.图2描述了三角自旋环中两个海森伯自旋之间的配对纠缠度C12随磁场强度B和温度T的变化情况.图2(a)是系统处于不同温度下配对纠缠度C12随磁场强度的变化关系.图2(a)的结果说明,当无外加磁场作用时,系统不存在纠缠.并且随着温度的提高,使系统产生纠缠的外加磁场强度也随之增加.就同一温度而言,配对纠缠度C12随着磁场强度的增加,对纠缠的作用是先促进,后抑制.如:当T=0.05时,无磁场(B=0)时,C12=0,直至B=0.02时,C12=0.001652(此处及以下在数值计算中,假定C12＜10−3时无纠缠),随着磁场强度逐渐增强,配对纠缠度迅速增加,达到最大配对纠缠度(B=0.38,C12=0.2886),随后配对纠缠度迅速下降直至消失.另外T=0.1和0.5时,曲线变化趋势与T=0.05相似,不同的是,使系统产生纠缠的外加磁场强度较高(当T=0.1时,B=0.07,C12=0.001094,而T=0.5时,B=2.71,C12=0.001178)和随着磁场强度增加产生的最大纠缠度较低(当T=0.1时,B=0.45,C12=0.1195,而T=0.5时,B=3.38,C12=0.01313).图2(b)是临界温度Tc随磁场强度B变化的相图,曲线与坐标轴围成的区域和曲线自身围成的区域是存在纠缠的区域.由图2(b)可知,系统纠缠受温度影响显著,并且存在纠缠的情况随磁场强度的变化是非连续性的,会存在多个纠缠恢复现象.由大的区域可知,当Tc＞0.65时,磁场对系统纠缠不再产生作用.对于温度较低时,如Tc=0.15时,纠缠仅存在于区域0.34≤B≤1.12和2.58≤B≤3.46,因此存在多个纠缠恢复现象.

3.2 XXZ-海森伯模型

现在,考虑海森伯自旋相互作用为XXZ模型(J=γ=K=1).图3(a)主图展现了在不同温度下,配对纠缠度C12随着磁场强度B变化情况,此处考虑Δ=2.而图3(a)右上角小图是当外加磁场B=2时,配对纠缠度C12在不同温度下随各向异性强度Δ的变化情况.与图2(a)比较发现,相同条件下,考虑各向异性能使系统产生更大的配对纠缠度,且当温度较低时出现一段稳定的平台区.当温度T=0.05时,最大配对纠缠度C12为0.3333(1.9≤B≤ 3.11),温度T=0.1的纠缠情况与T=0.05情况相似.另外,图3(a)中也存在与图2(a)相似的情况,比如外加磁场会诱导纠缠的产生且温度越高所需的外加磁场强度越大.以温度T=0.5曲线变化情况为例,当B=0时,无纠缠产生,但随着磁场强度的增加,直至B=1.22(C12=0.001054)时,开始诱导并迅速使系统达到最大纠缠(C12=0.1518),并保持最大纠缠持续一段平台区(2.99≤B≤3.03),随后磁场强度的增强,会逐渐抑制纠缠的产生,最终使纠缠消失.另外从图3(a)右上小图可知,配对纠缠度C12不因各向异性强度的增强而单调增加,且随着温度的增加,达到最大纠缠度需要更强的各向异性.以图3(a)中温度T=0.1和0.5为例,温度T=0.1达到最大纠缠C12=0.3288时Δ=1.51,但T=0.5时达到最大纠缠C12=0.1091需要Δ=4.84.图3(b)是临界温度Tc随磁场强度B的变化情况.与图2(b)比较发现,考虑z方向存在各向异性能获得更广泛范围的纠缠区域(曲线与横轴围成的区域).另外还发现,当系统处于特定区域(0.44≤B≤0.82)内的磁场强度时,适度提高温度能使系统发生纠缠.

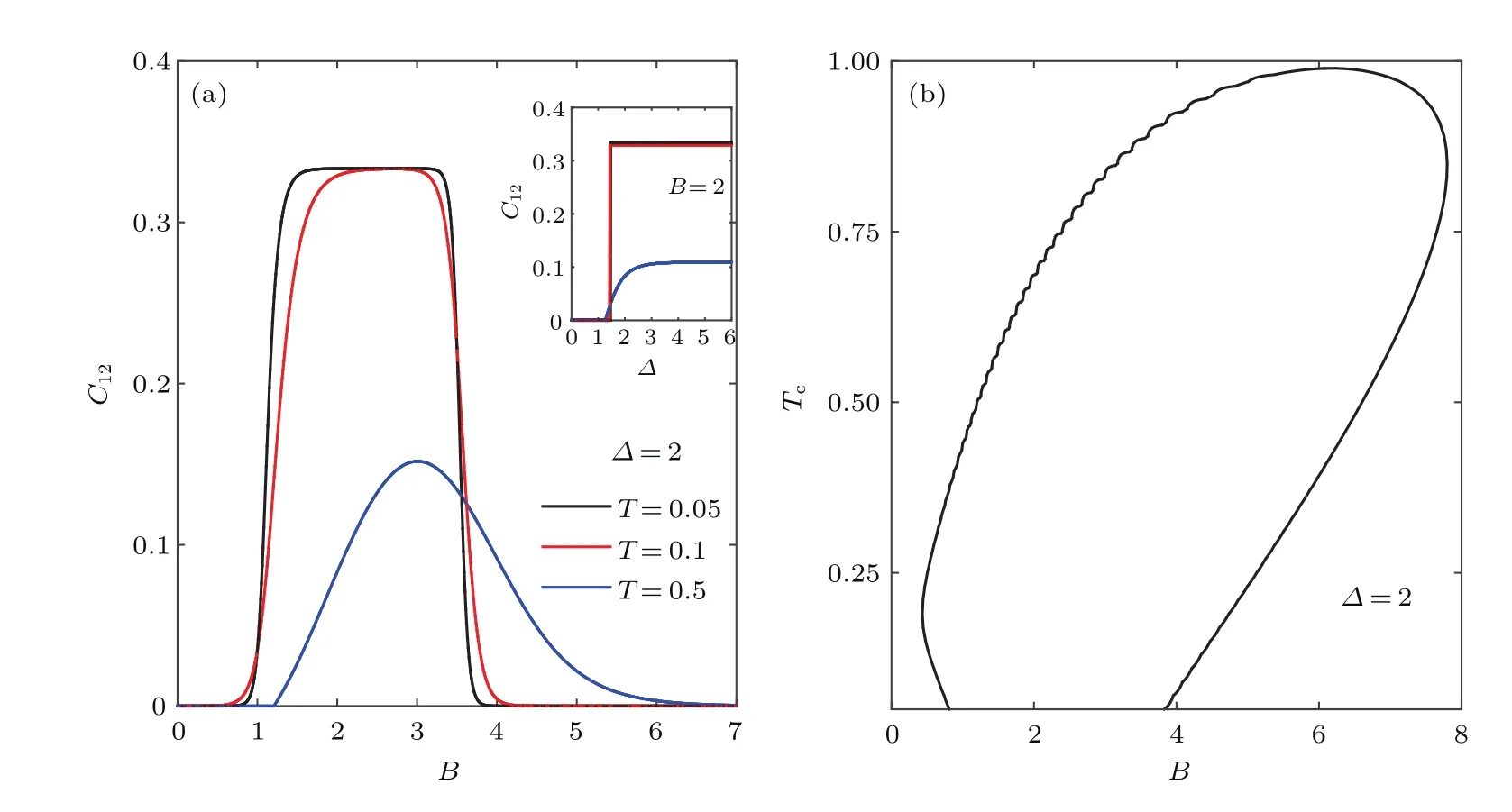
图3 (网刊彩色)配对纠缠度C12在不同温度下随磁场强度B和各向异性参数Δ的变化 (a)不同温度下,配对纠缠度C12随磁场强度B(各向异性参数Δ)的变化;(b)临界温度Tc随磁场强度B的变化Fig.3.(color online)The concurrence of Ising-Heisenberg chain with triangular plaquettes versus the magnetic field and anisotropy Δ with various temperatures:(a)the concurrence C12versus the magnitude of magnetic field B(anisotropy parameter Δ)for the different temperatures;(b)the critical temperature Tc versus the magnitude of magnetic field B.

3.3 XY Z-海森伯模型

最后,考虑考虑海森伯自旋相互作用为XY Z模型.图4展现了当系统处于各向异性XY Z海森堡模型时,配对纠缠度C12随着磁场强度B和温度T的变化情况.分别考虑y方向的各向异性强度大于z方向的各向异性强度(即γ＞Δ)和z方向的各向异性强度大于y方向的各向异性强度(即Δ＞γ)两种情况,如图4(a)—(d)所示.首先讨论γ＞Δ这一情况.图4(a)和图4(b)是当J=K=1,γ=3,Δ=2时配对纠缠度C12随磁场强度和温度的变化情况.与图3(a)相似,一定强度的外加磁场能诱导纠缠的产生,随着磁场强度的增大,反而抑制纠缠的产生,但有趣的是随着磁场强度继续增强,与图3(a)的区别是外加磁场会再次诱导纠缠的产生,并且在较高的温度下,增强外加磁场强度仍诱导系统纠缠的产生.以图4(a)中温度T=0.1曲线为例,磁场强度B＜0.63时无纠缠,当B=0.63时C12=0.00102.随着B逐渐增强,C12随之增大至最大纠缠0.3329(B=2.47),紧接着与图3(a)情况一样经历一段平台区,之后迅速下降直至C12=0(B=4.01),但当B≥4.11时,纠缠再次产生,且随着磁场强度加强,纠缠强度会再次出现第二个峰值C12=0.1252并持续一段小平台区(4.5≤B≤4.53),随后缓慢下降.另外,由图4(b)三维图可知,当温度T=1.1时,B≥7.1时仍能使系统产生纠缠,对于更高的温度,使系统产生纠缠所需的外加磁场强度更强.最后讨论图4(c)和图4(d)处于Δ＞γ这一情况下,配对纠缠度C12随磁场强度和温度的变化情况.发现当系统处于较高温度时,与γ＞Δ情况相比较，Δ＞γ的情况能诱导更高的纠缠度.以温度T=0.5为例,当系统处于γ＞Δ这一情况时,随着磁场强度的增加达到最大纠缠度C12=0.1906,而对于情况Δ＞γ最大纠缠度C12=0.2552.

图5描述了系统中海森伯自旋相互作用分别处于y方向的各向异性强度大于z方向的各向异性强度情况(J=K=1,γ=3,Δ=2)以及z方向的各向异性强度大于y方向的各向异性强度情况(J=K=1,γ=2,Δ=3)下,临界温度Tc随磁场强度的变化情况.图5中变化曲线与坐标轴围成的区域是纠缠区域,否则为非纠缠区域.从图5中明显可知,当磁场较小时,红线表示的情况(即J=K=1,γ=2,Δ=3)能获得更大的临界温度(即纠缠范围更广).另外,值得注意的是,当磁场强度较大时,两者都能获得较大的临界温度.有意思的是,两种各向异性的情况下系统处于特定磁场强度内都出现多个临界温度的情况,这说明在一定磁场强度下,提高温度会使系统纠缠恢复.以黑线表示的情况(J=K=1,γ=3,Δ=2)为例,当B=4.5,Tc＜0.27时系统存在纠缠,但0.27≤Tc≤0.43时,系统纠缠消失,而当0.43＜Tc＜1.09时,系统纠缠恢复.

图4 (网刊彩色)配对纠缠度C12随磁场强度B和温度T的变化 (a)和(b)对应J=K=1,γ=3,Δ=2;(c)和(d)对应J=K=1,γ=2,Δ=3Fig.4.(color online)The concurrence of Ising-Heisenberg chain with triangular plaquettes versus the magnetic field and temperature:(a)and(b)Correspond to the case with J=K=1,γ=3,Δ=2;(c)and(d)correspond to the case with J=K=1,γ=2,Δ =3.

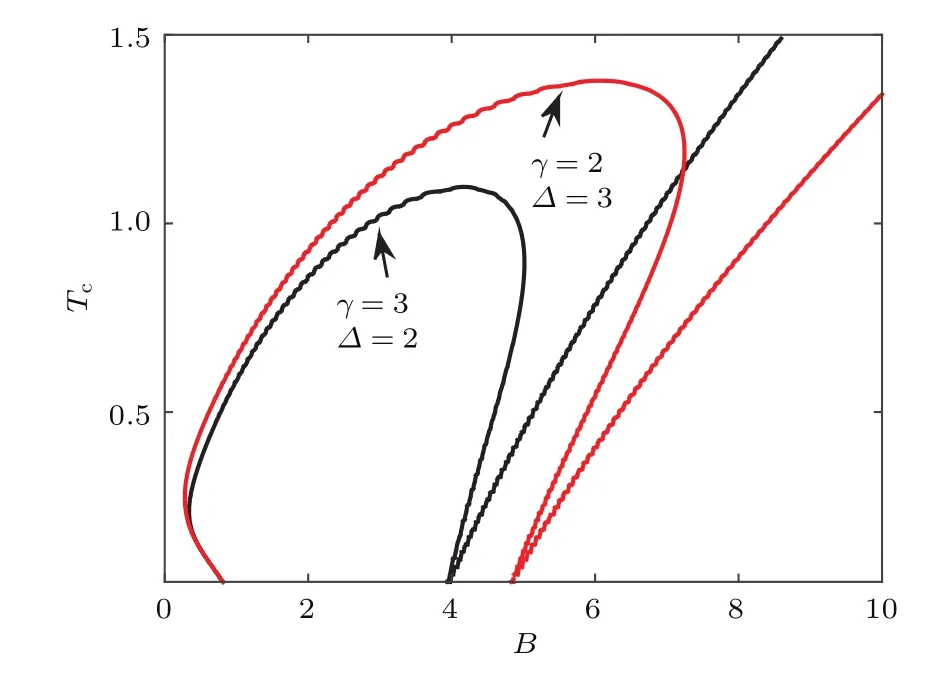
图5 (网刊彩色)临界温度Tc随磁场强度B的变化 (黑线对应γ=3和Δ=2的情况,红线对应γ=2和Δ=3的情况)Fig.5.(color online)The critical temperature versus the magnitude of magnetic field(the black line corresponds to the case with γ =3 and Δ =2,the red line to the case with γ =2 and Δ =3).

4 结 论

基于转移矩阵方法,通过数值计算求解配对纠缠度C12,研究了具有三角自旋环的伊辛-海森伯链的热纠缠性质.分别讨论了三角自旋环中自旋1/2粒子间具有XXX,XXZ和XY Z海森伯相互作用的三种模型.研究发现,系统处于XXX海森伯模型时,热纠缠受温度影响较为显著,外加一定强度的磁场能促进纠缠的产生;当系统处于XXZ和XY Z各向异性时,低温情况下,在一定的外加磁场作用下均能使系统获得较大纠缠度,而当温度较高时,系统处于XY Z各向异性的情况更能克服外界温度对系统纠缠的影响,尤其是系统处于z方向各向异性强度大于y方向各向异性强度的情况下的XY Z海森伯系统表现更为明显.另外,分析临界温度随磁场强度的变化情况,发现在特定的参数区域出现纠缠恢复现象.因此选择适当的温度和磁场强度,可以有效调节具有三角自旋环的伊辛-海森伯链的热纠缠性质.

[1]Misguich G,Lhuillier C 2004Frustrated Spin Systems(Singapore:World Scienti fic)p229

[2]Lee S H,Kikuchi H,Qiu Y,Lake B,Huang Q,Habicht K,Kiefer K 2007Nature Mater.6 853

[3]Moessner R,Sondhi S L 2001Phys.Rev.B63 224401

[4]Schmidt B,Shannon N,Thalmeier P 2006J.Phys.:Conf.Ser.51 207

[5]Zhitomirsky M E,Honecker A,Petrenko O A 2000Phys.Rev.Lett.85 3269

[6]Lee S,Lee K C 1998Phys.Rev.B57 8472

[7]Choi K Y,Matsuda Y H,Nojiri H,Kortz U,Hussain F,Stowe A C,Ramsey C,Dalal N S 2006Phys.Rev.Lett.96 107202

[8]Trif M,Troiani F,Stepanenko D,Loss D 2008Phys.Rev.Lett.101 217201

[9]Kubo K 1993Phys.Rev.B48 10552

[10]Nakamura T,Saika Y 1995J.Phys.Soc.Jpn.64 695

[11]Nakamura T,Kubo K 1996Phys.Rev.B53 6393

[12]Chen S,Büttner H,Voit J 2003Phys.Rev.B67 054412

[13]Guo Y P,Liu Z Q,Xu Y L,Kong X M 2016Phys.Rev.E93 052151

[14]Collins M F,Petrenko O A 1997Can.J.Phys.75 605

[15]Lecheminant P,Bernu B,Lhuillier C,Pierre L,Sindzingre P 1997Phys.Rev.B56 2521

[16]Waldtmann C,Everts H U,Bernu B,Lhuillier C,Sindzingre P,Lecheminant P,Pierre L 1998Eur.Phys.J.B2 501

[17]Mila F 1998Phys.Rev.Lett.81 2356

[18]Mambrini M,Trébosc J,Mila F 1999Phys.Rev.B59 13806

[19]Totsuka K,Mikeska H J 2002Phys.Rev.B66 054435

[20]Rojas O,Alcaraz F C 2003Phys.Rev.B67 174401

[21]Rojas O,Rojas M,Ananikian N S,de Souza S M 2012Phys.Rev.A86 042330

[22]Abgaryan V S,Ananikian N S,Ananikyan L N,Hovhannisyan V V 2015Solid State Commun.224 15

[23]Baxter R J 1982Exactly Solved Models in Statistical Mechanics(New York:Academic Press)p89

[24]Hida K 1994J.Phys.Soc.Jpn.63 2359

[25]Ohanyan V,Ananikian N S 2003Phys.Lett.A307 76

[28]Antonosyan D,Bellucci S,Ohanyan V 2009Phys.Rev.B79 014432

[29]Ohanyan V 2010Phys.Atom.Nucl.73 494

[30]Arnesen M C,Bose S,Vedral V 2001Phys.Rev.Lett.87 017901

[31]Wang X 2001Phys.Rev.A64 012313

[32]Wang X 2001Phys.Lett.A281 101

[33]Kamta G L,Starace A F 2002Phys.Rev.Lett.88 107901

[34]Zhou L,Song H S,Guo Y Q,Li C 2003Phys.Rev.A68 024301

[35]Gunlycke D,Kendon V M,Vedral V,Bose S 2001Phys.Rev.A64 042302

[36]Terzis A F,Paspalakis E 2004Phys.Lett.A333 438

[37]Canosa N,Rossignoli R 2004Phys.Rev.A69 052306

[38]Xi X Q,Chen W X,Hao S R,Yue R H 2002Phys.Lett.A300 567

[39]Sun Y,Chen Y,Chen H 2003Phys.Rev.A68 044301

[40]Asoudeh M,Karimipour V 2005Phys.Rev.A71 022308

[41]Cao M,Zhu S 2005Phys.Rev.A71 034311

[42]Zhang G F,Li S S 2005Phys.Rev.A72 034302

[43]Wu K D,Zhou B,Cao W Q 2007Phys.Lett.A362 381

[44]Zhou B 2011Int.J.Mod.Phys.B25 2135

[45]Chen S R,Xia Y J,Man Z X 2010Chin.Phys.B19 050304

[46]Ren J Z,Shao X Q,Zhang S,Yeon K H 2010Chin.Phys.B19 100307

[47]Lu P,Wang J S 2009Acta Phys.Sin.58 5955(in Chinese)[卢鹏,王顺金 2009物理学报 58 5955]

[48]Zhang Y L,Zhou B 2011Acta Phys.Sin.60 120301(in Chinese)[张英丽,周斌 2011物理学报60 120301]

[49]Ananikian N S,Ananikyan L N,Chakhmakhchyan L A,Rojas O 2012J.Phys.:Condens.Matter24 256001

[50]Torrico J,Rojas M,de Souza S M,Rojas O,Ananikian N S 2014Europhys.Lett.108 50007

[51]Abgaryan V S,Ananikian N S,Ananikyan L N,Hovhannisyan V 2015Solid State Commun.203 5

[52]Qiao J,Zhou B 2015Chin.Phys.B24 110306

[53]Hill S,Wootters W K 1997Phys.Rev.Lett.78 5022

[54]Wootters W K 1998Phys.Rev.Lett.80 2245

[55]Coffman V,Kundu J,Wootters W K 2000Phys.Rev.A61 052306

Thermal entanglement of Ising-Heisenberg chain with triangular plaquettes∗

Zheng Yi-Dan Mao Zhu†Zhou Bin‡

(Faculty of Physics and Electronic Science,Hubei University,Wuhan 430062,China)

17 August 2017;revised manuscript

22 September 2017)

Quantum entanglement as an important resource in quantum computation and quantum information has attracted much attention in recent decades.The effect of temperature should be viewed as an external control in the preparation of entangled state,and the thermal entanglement of the Heisenberg spin model has been discussed intensively.Due to the quantum fluctuation and thermal effect,there have been found some interesting physical phenomena in the geometrically frustrated spin system at zero or a certain temperature.Meanwhile,the lattice spin system with triangular plaquettes is regarded as a general structure of magnetic material.In this paper,we theoretically analyze the thermal entanglement of Ising-Heisenberg chain with triangular plaquettes.The transfer matrix method is used to calculate numerically the thermal entanglement in the in finite Ising-Heisenberg chain.We consider three kinds of Heisenberg spin interaction models(i.e.,XXX-Heisenberg model,XXZ-Heisenberg model andXY Z-Heisenberg model),and discuss the effects of magnetic field and temperature on the three models,respectively.The results show that temperature and magnetic field have important effects on the three models.Meanwhile,it is found that theXXX-Heisenberg model is more sensitive than the anisotropy model(i.e.,XXZ-Heisenberg model orXY Z-Heisenberg model)when temperature rises.A certain magnetic field would promote the generation of the quantum entangled states in all the three cases when the thermal fluctuation suppresses the quantum effects of the systems.In addition,it is found that the entanglement ofXYZHeisenberg model is more robust than the others at a higher temperature,especially when the anisotropy along thezaxis is greater than that along theyaxis.We also plot the variations of the critical temperature with magnetic field in the three models.From the critical temperature-magnetic field phase diagrams,we can obtain the range of parameters in which the pairwise entanglement of the system exists.We also find that the entanglement revival behaviors may occur in a specific range of the parameters.Therefore,the properties of the thermal entanglement of Ising-Heisenberg chain with triangular plaquettes can be controlled and enhanced by choosing and using suitable parameters of magnetic field and temperature.

thermal entanglement,pairwise concurrence,Ising-Heisenberg chain,transfer matrix approach

PACS:03.65.UdDOI:10.7498/aps.66.230304

*Project supported by the National Natural Science Foundation of China(Grant No.11274102),the Program for New Century Excellent Talents in University of Ministry of Education of China(Grant No.NCET-11-0960),and the Specialized Research Fund for the Doctoral Program of Higher Education of China(Grant No.20134208110001).

†Corresponding author.E-mail:maozhu@hubu.edu.cn

‡Corresponding author.E-mail:binzhou@hubu.edu.cn

(2017年8月17日收到;2017年9月22日收到修改稿)

研究了具有三角自旋环的伊辛-海森伯链在磁场作用下的热纠缠性质.分别讨论了三角自旋环中自旋1/2粒子间相互作用的三种情形,即XXX,XXZ和XY Z海森伯模型.利用转移矩阵方法,数值计算了具有三角自旋环的伊辛-海森伯链的配对纠缠度.计算结果表明,外加磁场强度和温度对系统处于上述三种海森伯模型的热纠缠性质均有重要影响.给出了系统在不同的海森伯模型下,纠缠消失对应的临界温度随磁场强度的变化图,由此可以得到系统存在配对纠缠的参数区域,同时发现在特定的参数区域存在纠缠恢复现象.因此适当调节温度和磁场强度,可以有效调控具有三角自旋环的伊辛-海森伯链热纠缠性质.

10.7498/aps.66.230304∗国家自然科学基金(批准号:11274102)、教育部新世纪优秀人才支持计划(批准号:NCET-11-0960)和高等学校博士学科点专项科研基金(批准号:20134208110001)资助的课题.

†通信作者.E-mail:maozhu@hubu.edu.cn

‡通信作者.E-mail:binzhou@hubu.edu.cn