基于量子隐形传态的量子保密通信方案∗

杨璐 马鸿洋 郑超 丁晓兰 高健存 龙桂鲁6)

1)(清华大学物理系,低维量子物理国家重点实验室,北京 100084)

2)(通信网信息传输与分发技术重点实验室,石家庄 050081)

3)(青岛理工大学理学院,青岛 266033)

4)(北方工业大学理学院,北京 100144)

5)(重庆大学通信工程学院,重庆 400044)

6)(清华大学信息科学与技术国家实验室(筹),北京 100084)

基于量子隐形传态的量子保密通信方案∗

杨璐1)2)马鸿洋3)郑超4)丁晓兰5)高健存1)龙桂鲁1)6)†

1)(清华大学物理系,低维量子物理国家重点实验室,北京 100084)

2)(通信网信息传输与分发技术重点实验室,石家庄 050081)

3)(青岛理工大学理学院,青岛 266033)

4)(北方工业大学理学院,北京 100144)

5)(重庆大学通信工程学院,重庆 400044)

6)(清华大学信息科学与技术国家实验室(筹),北京 100084)

量子隐形传态通信,全用型量子密钥分发,确定性量子密钥分发,量子安全直接通信

1 引 言

利用物理性质保护信息安全是近年来的研究热点.例如利用荧光光学性质保护数据安全的黄加密方法[1],使以光作为载体的信息传输更为安全.量子通信利用量子力学原理保护信息传输安全,已经引起人们的广泛关注.量子通信可分为量子密钥分发(quantum key distribution,QKD)[2−24]、量子安全直接通信(quantum secure direct communication,QSDC)[25−43]、量子隐形传态[44−46]、量子密集编码[47,48]、量子秘密共享等[49−53]方向,其中量子密钥分发、量子安全直接通信和量子秘密共享以保护信息安全为目的,又叫作量子保密通信或量子密码学.实验研究中纠缠分发的安全距离已经达到1200 km[54],量子密钥分发的安全距离已经达到400 km[55],这些都为将来实现远距离量子通信及网络打下了坚实的基础[53].

量子密钥分发的代表性协议有基于单光子的BB84协议[2]及基于纠缠对的E91协议[3]和BBM92协议[4],量子安全直接通信的代表性协议有基于纠缠对的高效协议[25]、两步协议[26]和基于单光子的DL04协议[27].量子秘密共享是多个用户共享密钥[49],可以近似看作一对多的量子密钥分发.

量子隐形传态由Bennet等[44]于1993年提出,有大量的理论和实验研究[56−70].它可以不经过实物粒子的传输而将粒子的未知量子态传输到远方.这是量子体系特有的通信形式,没有经典对应.量子隐形传态可应用于构建量子网络的量子中继器和远程态制备等[71,72],有广泛而重要的应用.

本文对基于量子隐形传态的量子通信(简称量子隐形传态通信)方案进行了系统分析,并将其与量子密钥分发和量子安全直接通信进行对比,分析各个协议的特点.目前人们对利用量子隐形传态进行量子通信存在一些误解,如认为量子态的传输不受信道噪声的影响,且发送者与接收者之间的距离也不受限制,甚至有人认为可以用来作超光速通信.通过本文的分析,我们可以看到量子隐形传态在保密通信方面等价于包含了一个全用型量子密钥分发和一个经典通信的复合过程,并没有比量子密钥分发更有优势,而且其传输与中间介质和距离都有关系,不可能实现超光速通信.

2 量子隐形传态通信

2.1 量子隐形传态的一般原理

量子隐形传态由Bennet等[44]在1993年提出,利用EPR(Einstein-Podolsky-Rosen)纠缠对的长程关联,可实现未知量子态在发送者Alice与接收者Bob之间的传递.

首先由Alice制备粒子A和粒子B组成的EPR纠缠对[73],这些EPR纠缠对可处于以下四个贝尔态中的任意一个:

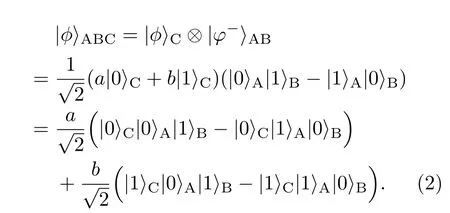
将其用A和C两粒子系统的贝尔态展开,则(2)式变换为

此时,Alice对粒子A和C进行联合贝尔基测量,则A,C两粒子体系的量子态将以1/4的概率坍缩为四个贝尔态中的任意一个,而Bob手中粒子B的量子态同时坍缩到对应的量子态上.之后Alice将联合贝尔基的测量结果告知Bob,Bob对应不同的测量结果,对手中的粒子采用不同的U操作,即可使粒子B处于原有未知态上,即实现了量子态的远程传递.贝尔基测量后A和C两粒子的状态粒子B的状态以及Bob根据Alice告知的贝尔基测量结果选择的U操作以使粒子B的状态达到原有的未知态的对应关系列于表1中. 其中量子态及操作的矩阵形式为

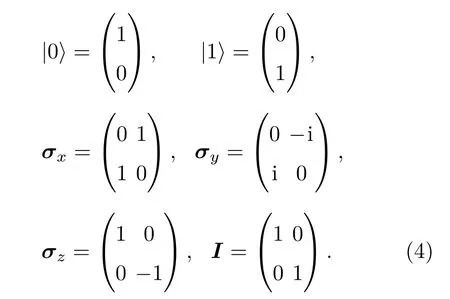
表1 量子隐形传态操作表[](若A,B粒子处于|φ−〉AB,当A,C粒子的贝尔基测量结果为第一栏时,对应粒子B的状态以及将其变换到粒子C原来状态的操作)Table 1.Operations of quantum teleportation[].On condition that the entangled pair of particles A and B is in the initial state|φ−〉AB,the results of the Bellbasis measurement of entangled pair of particles A and C which are in the first column,lead to different states that particle B is in,and the corresponding operations Bob takes to project them onto the initial state of particle C.

2.2 传输态为计算基矢态时量子隐形传态的单粒子操作

下面具体描述利用量子隐形传态进行量子通信的方案(以下简称量子隐形传态通信方案).当利用量子隐形传态进行保密通信时,单粒子的状态不再是未知的任意线性叠加态,而是计算基矢|0〉态或者|1〉态,此时相对于一般的量子隐形传态可以进行步骤简化.用|0〉和|1〉分别表示经典比特0和1,传输的信息为|0〉和|1〉组成的量子状态串.将2.1节中的未知态作为需要传输的信息,满足a=0,b=1或a=1,b=0,因此±a|0〉B±b|1〉B表示同一个态,±a|1〉B±b|0〉B也表示同一个态.这样对单粒子的操作由原来的四个减少到现在的两个,即不操作I,或者作σx操作.即当贝尔基测量之后粒子B的状态为±a|0〉B±b|1〉B时,Bob不需要对手中的粒子B作任何操作;当贝尔基测量之后粒子B的状态为±a|1〉B±b|0〉B时,Bob只需要对手中的粒子B作σx操作.根据2.1节的结果,从表1可以看出,当取值为|ψ+〉CA或|ψ−〉CA时,Bob对粒子B进行σx操作,即可得到当取值为|φ+〉CA或|φ−〉CA时,Bob对粒子B进行I操作,即此时粒子B的状态已经是

2.3 计算基矢量子态量子隐形传态的贝尔基测量

由于要传输的是计算基矢量子态|0〉态或|1〉态,因此作贝尔基测量时不需要区别四个贝尔态,只需要能够区别两类贝尔态即可.对应粒子A和C所有可取的初始态,为得到态Bob采用的具体操作如表2所示.我们采取以下统一写法: 将|ψ+〉AB和|ψ−〉AB统一写为|ψ±〉AB,同理可记|φ±〉AB,|ψ±〉CA和|φ±〉CA. 线性量子光学只能区分四个贝尔态中的两种,这正好满足量子隐形传态通信的需要.因此利用量子隐形传态进行保密通信可以在线性量子光学技术中实现.

表2 隐形传态通信方案中Bob采用的操作(对于A,B粒子初始时处于|ψ±〉AB或|φ±〉AB的不同情况,当A,C粒子的贝尔基测量结果为|ψ±〉CA或|φ±〉CA时,Bob采取的对应操作将粒子B的状态变换到粒子C原来的状态)Table 2.Operations of Bob in quantum communication using quantum teleportation.On condition that the entangled pair of particles A and B is in the initial state|ψ±〉ABor|φ±〉AB,when the results of the Bell-basis measurement of entangled pair of particles A and C are|ψ±〉CAor|φ±〉CA,the corresponding operations Bob takes to project the state that particle B is in onto the initial state of particle C are in the table.

2.4 量子隐形传态通信方案的具体步骤

步骤1首先Alice制备N个处于量子态的EPR纠缠对,并从每个纠缠对中挑出一个,组成粒子序列SA,剩下的粒子组成序列SB,并经量子信道发送给Bob.

步骤2Bob从SB中随机抽取一部分粒子以(|0〉,|1〉)基矢或者(|+〉,|−〉)基矢作单粒子测量,并将测量基矢和结果通过公开信道告知Alice.Alice对SA中对应的粒子采用与Bob相同的基矢作单粒子测量,并与Bob的结果进行比较,判断SB序列的传输是否安全.这是传输过程中的安全性检测,当测量结果的出错率低于设定的安全阈值时,认为传输是安全的,继续进行后续信息传输步骤,否则放弃传输.这一步骤完成了量子纠缠的安全分发.很显然,在这一步骤中,纠缠的分发受到粒子A和B之间介质的影响,也与它们之间的距离有关.这里所用的有序粒子序列传输方法即为文献[25]首先提出的量子块传输方法.

步骤3Alice将要传输的信息,即由0和1组成的随机序列,编码为由|0〉和|1〉组成的量子状态序列SC,SC包含的粒子数应与从SA中抽取粒子作测量后剩下的粒子组成序列的粒子数相等.Alice将SC和中的粒子两两对应作简化的联合贝尔基测量,即只需要区分四个贝尔态中的两类即可,并将测量的结果通过公开信道告知Bob.可以看到,为了使Bob读取信息,Alice必须传输经典信息,即为了读出1 bit的信息,Alice必须传给Bob 1 bit的经典信息,以便Bob完成下一步操作.在这一步骤中,没有量子信道的传输,不存在Eve对量子信道的破坏.假设经典信道不被破坏.这解释了有些非专业人士误认为量子隐形传态通信不受通信距离和两者之间介质影响的原因.我们已经看到,量子纠缠分发和传输贝尔基测量结果的经典通信都会受到传输距离和中间介质的影响.同时虽然贝尔基测量造成的量子态塌缩是瞬时的、超光速的,但是为了读取信息,还需要传输贝尔基测量结果的经典通信,因此量子隐形传态通信也不是超光速的.

步骤4Bob手中粒子组成的序列在Alice作贝尔基测量后塌缩到了相应的单粒子态,Bob根据Alice传输的简化联合贝尔基测量结果,对应表2中的操作对中的粒子作σx或I操作,即将Alice想传输的信息量子态传输到粒子序列中,再对每个粒子作单粒子测量,即可读出信息.

3 量子隐形传态通信与其他量子通信协议的对比

3.1 量子隐形传态通信与全用型量子密钥分发和经典通信复合过程的等价性

量子密钥分发是在通信双方间产生量子信道并通过量子信道传输密钥,在该过程中,根据安全性检测的结果,确认传输过程是否安全;在密钥已经安全分发的情况下,再通过一次额外的经典通信,将明文用量子密钥加密后进行传输,最终实现通信.其代表性协议有上文提及的BB84协议[2],E91协议[3]和BBM92协议[4],学者们对其进行了广泛的研究[5−24,55].

根据信息载体数量的使用比例,可以将量子密钥分发分成全用型和分用型.全用型指的是除了用于窃听检测以外的载体,剩余的信息载体都可以用来进行密钥分发;分用型量子密钥分发指的是剩余的载体只有一部分载体粒子可以用来进行密钥分发.例如BB84量子密钥协议[2]就是一个分用型量子密钥分发协议,除用作窃听检测的那部分单光子外,通信双方选取不同测量基对应的那些光子都直接舍弃,不用作密钥.而量子隐形传态通信中,贝尔基测量之后,有两类贝尔基测量结果,这个结果可以看作密钥,每个测量结果都可以用作密钥,因此这是一种全用型量子密钥分发.全用型量子密钥分发不一定是确定性量子密钥分发.确定性量子密钥分发就是可以事先确定密钥,然后确定性地传输给对方.所有确定性量子密钥分发都是全用型量子密钥分发.以下列举的是全用型量子密钥分发,但不是确定性量子密钥分发:Alice和Bob安全地进行量子纠缠分发之后,共有一系列处于贝尔态的EPR纠缠对,Alice和Bob分别对手里的粒子进行计算基矢的测量,得到的结果是随机的0或1,是不确定的,但是每个EPR对的测量结果都可以作为密钥使用,因而是全用型的.

在量子隐形传态通信中,可以将贝尔基测量之后Bob手中粒子塌缩后的态看作经过密钥加密后的密文,将Alice作的贝尔基测量结果看作密钥.当Alice通过经典信道将密钥传给Bob后,Bob对手中的粒子作σx或I操作之后进行测量即可得到信息,这相当于对密文进行解码.如果改变Bob的操作和测量顺序,即先测量再作操作,则这种对应更加明显:Alice对共享的EPR序列进行简化贝尔基测量之后,Bob得到了一个0和1组成的密文序列,Bob再根据Alice传送的贝尔基测量结果的密钥序列,使原先序列中相应的数字不变或者改变,即将密文与密钥作二进制加法,即可得到信息.可见量子隐形传态通信是一个全用型量子密钥分发再加经典通信的复合过程,其中由贝尔基测量导致Bob手中的粒子塌缩成一系列单粒子态,相当于全用型量子密钥分发传输密文,而关于贝尔基测量结果的经典通信传输的是密钥.这与量子安全直接通信不同,后者不需要额外的经典信息的传输来读出秘密信息,秘密信息在量子信道中直接进行传输[75].

3.2 量子隐形传态通信方案中介质和距离的影响

量子隐形传态通信方案会受到传输介质和距离的影响,因为该方案包含纠缠对的产生和分发、联合贝尔基测量和经典通信这三个主要过程.尽管贝尔基测量时量子态的塌缩不受Alice和Bob之间介质以及二者之间距离的影响,但是在之前的量子纠缠分发中,这两个因素都有影响,与量子密钥分发和量子安全直接通信所受到的影响是相同的.之所以会有误解,主要是因为量子隐形传态中事先假设量子纠缠已经完成了安全的分发.

纠缠分发可选用自由空间[76]或通信光纤[77]两种信道,但受限于传输过程中的衰减和噪声等[78],例如在距离超过1000 km的纠缠分发实验中,信道衰减总在20 dB以上[79−81],所以纠缠态的光子通常并不直接进行长距离传输,而是利用量子中继器实现多节点远距离传输[82],众多学者都在研究如何分发高保真度的纠缠粒子[83−85].文献[78]提到,由于近地面大气损耗和湍流以及地球曲率等因素,量子纠缠分发的传输距离被限制在百千米量级,但光子在外太空的衰减几乎为零,基于空间平台的量子通信被公认为是最切实可行的技术途径之一.我国“墨子号”量子卫星的成功发射也证明了这一点,但如上所述,要想利用隐形传态实现通信,必须考虑信道中的衰减和噪声.

例如在纠缠分发过程中会发生退相干现象,其原因为测量影响和环境作用[86].文献[87]指出,将光子的极化自由度用作量子比特时,其在通信传送过程中会受到热涨落、介质不均匀性和光纤中双折射现象的影响,这些影响可近似为一种酉噪声[88]:

式中|↔〉和|↕〉分别表示光子的水平极化态和竖直极化态,Δ、α和θ为随时间波动的酉噪声的参数.

由于光子的传输速度很快,可认为时间(空间)间隔很短的几个光子或波包在同一噪声信道中传输时受到的影响是相同的,具有这种性质的酉噪声称为联合酉噪声[89].

根据(4)式中参数的不同取值,常见的主要联合酉噪声信道有联合比特反转噪声信道(θ=π/2,Δ=α=0)、联合退相位噪声信道(θ=0,Δ和α取任意值)和联合旋转噪声信道(θ取任意值,Δ=α=0).

光子的极化自由度、频率自由度和空间自由度,都可用作量子比特的信息载体.光子的极化自由度容易受到噪声的影响,频率自由度和空间自由度相对不易受噪声的影响.所以可以在光子进入噪声信道前将极化自由度所携带的信息转码到频率或空间自由度上,等到传输结束,再将信息转码回到极化自由度,可在一定程度上消除噪声的不利影响[90].

文献[91—96]讨论了如何在噪声信道中实现纠缠分发,文献[94]给出了一个利用频率自由度分发贝尔态的方案,文献[95]给出了一个利用空间自由度在联合比特反转噪声信道中分发贝尔态的方案,文献[96]给出了一个利用空间自由度在联合噪声信道中分发χ类纠缠态的方案.

此外,量子隐形传态通信方案中传输贝尔基测量结果的经典通信也会受到介质和距离的影响.例如经典的无线微波通信实际上在低层大气而不是均匀介质的自由空间中传播,不仅受到地球曲率的影响,还会受到大气层反射、折射、散射和吸收等的影响,从而产生损耗.而基于微波中继通信和空间技术发展起来的卫星通信,实际上是设在地面上空的微波中继站.卫星通信的传输损耗包括自由空间传播损耗(与卫星和接收站之间距离的二次方成正比)、大气吸收和雾雨的损耗;微波频段的噪声主要由热噪声——电子在导体中不规则运动所致;外部噪声包括宇宙、大气、降雨以及天线旁瓣收到的大地噪声等[97].而有线通信中的光纤通信在传输过程中需要考虑传输损耗,包括光纤材料的吸收与散射损耗、光纤的微弯与宏弯辐射损耗、光纤的连接与耦合损耗等[98],以上都会受到传输距离以及光纤铺设具体环境的影响.所以尽管贝尔基测量和量子态塌缩过程不受介质的影响,但水下潜艇与天上卫星的经典通信依然受到大气层和海水介质的影响.

在实际的通信中,考虑到噪声的存在,可以利用纠缠纯化来提高信道的纠缠度及纠缠转移以降低量子信道的损耗[26],也可以考虑利用编码进行噪声环境下的传输[32].

3.3 量子隐形传态通信方案的安全性分析

在量子隐形传态通信之前,纠缠分发已经完成.在作贝尔基测量时,量子态的塌缩分别发生在Alice的场地(贝尔态塌缩)和Bob的场地(单粒子态塌缩),在这一过程中窃听者没有任何机会进行窃听.后面的经典通信告知Bob相应的贝尔态测量结果,窃听者虽然也能听到,但得不到任何信息.因此量子隐形传态通信的安全性完全取决于之前的量子纠缠分发,即Alice和Bob共享纠缠的EPR对的分发.在量子隐形传态中,这是假设已经完成的.实际上需要通过块传输技术来实现,即将大量纠缠对中的一个粒子留在Alice手中,将另一个粒子发送给Bob,再从中挑选部分粒子进行单粒子测量,通过Alice和Bob的比对来判断这一纠缠分发过程是否被窃听,这与量子安全直接通信中的块传输相同.因此量子隐形传态通信的安全性与量子安全直接通信的安全性是一致的.量子密钥分发的安全性不依赖于块传输,它是将单光子一个一个地发送、测量,直到大量单光子完成量子密钥分发之后才能从中挑选出部分结果进行比对来发现是否有窃听,如果有窃听,则此时已传输数据的大部分已经泄露.因此量子密钥分发只能先传输随机数据,确认没有窃听之后再将其作为密钥,发现有窃听则将所传输的数据放弃,这样可保证安全性.

3.4 量子隐形传态通信与基于纠缠的量子保密通信方案的比较

量子隐形传态通信方案和量子密钥分发的E91协议[3]和BBM92协议[4],都利用EPR对的纠缠特性.在量子隐形传态通信方案中,在贝尔基测量时密文已经瞬间分发给Bob,但需把作为密钥的联合贝尔基测量结果通过经典通信告诉Bob.在E91协议[3]和BBM92协议[4]中,采用单粒子测量产生密钥,并通过量子信道进行安全分发,之后同样也需要额外的经典通信来传输密文方可完成通信.尽管在计算基矢态下的贝尔基测量可以在线性光学技术中实现,但通过实验实现联合贝尔基测量较单光子探测更为困难.对比两类保密通信方案的效率,在E91协议[3]和BBM92协议[4]中,由于Alice和Bob作单光子测量时随机采用两种基矢中的一种,双方采用相同测量基矢的概率为1/2,因此其效率是量子隐形传态通信方案的一半.这主要是由于在E91协议[3]和BBM92协议[4]中没有使用量子存储,如果使用量子存储,E91协议[3]和BBM92协议[4]的效率就和量子隐形传态通信方案一样[24].如果使用量子存储,与量子隐形传态通信的情况相同,完全可以在量子纠缠分发之后Alice和Bob都对手中的粒子在σz基下进行测量,将测量结果作为密钥使用,然后Alice通过经典通信将密文发送给Bob.这样做比量子隐形传态通信更加简单,因为只需要进行单光子探测,不需要进行复杂的贝尔基测量.

在量子信道数据性质方面,隐形传态通信传输的是作为密文的塌缩量子态,量子密钥分发传输的是密钥;在密钥读出方式方面,隐形传态通信采取贝尔基测量,量子密钥分发采用单光子测量;在信息的传递方式方面,二者都需采用额外的经典通信,才能完成最终的通信;在携带数据量方面,二者都是一个EPR对可传送1 bit数据.

将量子隐形传态通信方案与量子安全直接通信的高效方案[25]和两步方案[26]进行对比.在高效方案[25]和两步方案[26]中,在量子信道中直接传送秘密信息,不需密钥;同时在保证量子纠缠分发安全后,即Alice和Bob手中各有EPR对中的一个粒子以后,Alice将手中的粒子直接送给Bob(高效方案),或者经过密集编码操作之后送给Bob(两步方案),这时每个EPR对可以传送2 bit信息,而量子隐形传态通信只能传输1 bit信息.在大气中量子信号的损耗比较大,而在卫星所在的太空中量子信号的损耗很小,这种情况下采用量子安全直接通信是更好的选择.

在量子信道数据性质方面,隐形传态通信传输的是作为密文的塌缩量子态,量子安全直接通信传输的是秘密信息;在密钥读出方式方面,隐形传态通信采取贝尔基测量,量子安全直接通信无需密钥;在信息的传递方式方面,隐形传态通信还需采用额外的经典通信;在携带数据量方面,隐形传态通信中一个EPR对传送1 bit数据,高效或两步方案中一个EPR对可传送2 bit数据.

将量子隐形传态通信方案与经典通信的一次性便笺密码方案[99]进行对比.经典通信方案需要发送者和接收者采用经典加密的方式提前生成密钥并分别携带.经典密码有丢失的危险.经典密码的携带和保存比量子态的携带和保存容易得多,但是所携带的经典密钥会很快消耗完.如果需传输的数据量并不很大,则可考虑采用这种携带经典密码的方式.而量子隐形传态通信、量子密钥分发、量子安全直接通信可以不停地生成密钥,并且量子安全直接通信不仅可以生成密钥,还可以直接传输秘密信息.

在量子信道数据性质方面,隐形传态通信传输的是作为密文的塌缩量子态;在密钥读出方式方面,隐形传态通信采取贝尔基测量,经典一次便笺方案提前生成密钥并且双方分别携带;在信息的传递方式方面,隐形传态通信还需采用额外的经典通信,经典一次便笺方案采用经典加密传输信息;在携带数据量方面,二者都是1 bit数据可传送1 bit信息.

多个方案的参数对比如表3所示.

表3 量子隐形传态通信方案与其他方案的对比Table 3.The comparison between quantum communication using quantum teleportation and other protocols.

4 结 论

在量子通信中,与量子密钥分发方案相比,量子隐形传态通信方案密文的传输在作贝尔基测量时瞬时完成,但仍然需要将联合贝尔基测量结果作为密钥并进行一次经典通信,贝尔基测量比较困难,窃听者得不到密文,但是可以得到经典信道传输的密钥;利用量子密钥分发进行通信时,在量子密钥分发完成后,也需要再进行一次经典通信才能最终完成秘密信息的传递,窃听者得不到密钥,但是可以得到经典信道传输的密文,这与量子隐形传态通信的原理相同.由于在量子密钥分发中一般采用单粒子测量,因此量子密钥分发的实现比量子隐形传态通信容易.量子隐形传态通信方案与量子安全直接通信的两步方案相比,量子隐形传态通信的纠缠分发只需要经过一次量子信道,损耗较小;而两步方案中需要两个光子都进行量子传输,损耗更大,但是每个EPR对携带2 bit信息,信息容量增大了一倍.由于在太空中量子信道的损耗较小,使用量子安全直接通信更好.

[1]Sun H B,Liu S J,Lin W P,Zhang K Y,Lü W,Huang X,Huo F W,Yang H R,Jenkins G,Zhao Q,Huang W 2014Nat.Commun.4 3601

[2]Bennett C H,Brassard G 1984Proceedings of IEEE International Conference on Computers,System and Signal Processing(Bangalore:IEEE)p175

[3]Ekert A K 1991Phys.Rev.Lett.67 661

[4]Bennett C H,Brassard G,Mermin N D 1992Phys.Rev.Lett.68 557

[5]Deng F G,Long G L 2003Phys.Rev.A68 042315

[6]Deng F G,Long G L 2004Phys.Rev.A70 012311

[7]Li X H,Deng F G,Zhou H Y 2008Phys.Rev.A78 022321

[8]Beige A,Englert B G,Kurtsiefer C,Weinfurter H 2002Acta Phys.Pol.A101 357

[9]Yan F L,Zhang X 2004Eur.Phys.J.B41 75

[10]Gao T,Fan F L,Wang Z X 2005J.Phys.A38 5761

[11]Man Z X,Zhang Z J,Li Y 2005Chin.Phys.Lett.22 22

[12]Zhu A D,Xia Y,Fan Q B,Zhang S 2006Phys.Rev.A73 022338

[13]Lee H,Lim J,Yang H 2006Phys.Rev.A73 042305

[14]Wang J,Zhang Q,Tang C J 2006Int.J.Quantum Inf.4 925

[15]Wang J,Zhang Q,Tang C J 2006Int.J.Mod.Phys.C17 685

[16]Wang H F,Zhang S,Yeon K H,Um C I 2006J.Korean Phys.Soc.49 459

[17]Chang Y,Zhang S B,Yan L L,Li J 2014Chin.Sci.Bull.59 2835

[18]Li X H,Deng F G,Li C Y,Liang Y J,Zhou P,Zhou H Y 2006J.Korean Phys.Soc.49 1354

[19]Gao G,Fang M,Yang R M 2011Int.J.Theor.Phys.50 882

[20]Zhang C M,Li M,Yin Z Q,Li H W,Chen W,Han Z F 2015Sci.China Phys.Mech.Astron.58 590301

[21]Wu C F,Du Y N,Wang J D,Wei Z J,Qin X J,Zhao F,Zhang Z M 2016Acta Phys.Sin.65 100302(in Chinese)[吴承峰,杜亚男,王金东,魏正军,秦晓娟,赵峰,张智明2016物理学报65 100302]

[22]Sun Y,Zhao S H,Dong C 2015Acta Phys.Sin.64 140304(in Chinese)[孙颖,赵尚弘,东晨 2015物理学报64 140304]

[23]An X B,Yin Z Q,Han Z F 2015Acta Phys.Sin.64 140303(in Chinese)[安雪碧,银振强,韩正甫2015物理学报64 140303]

[24]Deng F G,Long G L,Wang Y,Xiao L 2004Chin.Phys.Lett21 2097

[25]Long G L,Liu X S 2002Phys.Rev.A65 032302

[26]Deng F G,Long G L,Liu X S 2003Phys.Rev.A68 042317

[27]Deng F G,Long G L 2004Phys.Rev.A69 052319

[28]Wang C,Deng F G,Li Y S,Liu X S,Long G L 2005Phys.Rev.A71 044305

[29]Wang C,Deng F G,Long G L 2005Opt.Commun.253 15

[30]Li X H,Li C Y,Deng F G,Zhou P,Liang Y J,Zhou H Y 2007Chin.Phys.16 2149

[31]Zhang W,Ding D S,Sheng Y B,Zhou L,Shi B S,Guo G C 2016 arXiv:1609.09184

[32]Hu J Y,Yu B,Jing M Y,Xiao L T,Jia S T,Qin G Q,Long G L 2016Light Sci.Appl.5 e16144

[33]Deng F G,Ren B C,Li X H 2017Sci.Bull.62 46

[34]Gu B,Huang Y G,Fang X,Zhang C Y 2011Chin.Phys.B20 100309

[35]Ma H Y,Qin G Q,Fan X K,Chu P C 2015Acta Phys.Sin.64 160306(in Chinese)[马鸿洋,秦国卿,范兴奎,初鹏程2015物理学报64 160306]

[36]Yang Y G 2013Research on Protocols of Quantum Cryptography:Design and Analysis(Beijing:Science Press)pp60–88(in Chinese)[杨宇光 2013量子密码协议的设计和分析 (北京:科学出版社)第60—88页]

[37]Zhao X L,Li J L,Niu P H,Ma H Y,Ruan D 2017Chin.Phys.B26 030302

[38]Ren B C,Wei H R,Hua M,Li T,Deng F G 2013Eur.Phys.J.D67 30

[39]Cao Z W,Zhao G,Zhang S H,Feng X Y,Peng J Y 2016Acta Phys.Sin.65 230301(in Chinese)[曹正文,赵光,张爽浩,冯晓毅,彭进业2016物理学报65 230301]

[40]Banerjee A,Pathak A 2012Phys.Lett.A376 2944

[41]Pirandola S,Braunstein S L,Mancini S,Lloyd S 2008Eur.Phys.Lett.84 20013

[42]Meslouhi A,Hassouni Y 2013Quantum Inf.Process.12 2603

[43]Zheng C,Long G F 2014Sci.China Phys.Mech.Astron.57 1238

[44]Bennett C H,Brassard G,Crepeau C,Jozsa R,Peres A,Wootters W K 1993Phys.Rev.Lett.70 1895

[45]Karlsson A,Bourennane M 1998Phys.Rev.A58 4394

[46]Li X H,Ghose S 2015Phys.Rev.A91 012320

[47]Bennett C H,Wiesner S J 1992Phys.Rev.Lett.69 2881

[48]Liu X S,Long G L,Tong D M,Li F 2002Phys.Rev.A65 022304

[49]Hillery M,Bužek V,Berthiaume A 1999Phys.Rev.A59 1829

[50]Karlsson A,Koashi M,Imoto N 1999Phys.Rev.A59 162

[51]Xiao L,Long G L,Deng F G,Pan J W 2004Phys.Rev.A69 052307

[52]Deng F G,Zhou H Y,Long G L 2006J.Phys.A39 14089

[53]Li X H 2015Acta Phys.Sin.64 160307(in Chinese)[李熙涵2015物理学报64 160307]

[54]Yin J,Cao Y,Li Y H,Liao S K,Zhang L,Ren J G,Cai W Q,Liu W Y,Li B,Dai H,Li G B,Lu Q M,Gong Y H,Xu Y,Li S L,Li F Z,Yin Y Y,Jiang Z Q,Li M,Jia J J,Ren G,He D,Zhou Y L,Zhang X X,Wang N,Chang X,Zhu Z C,Liu N L,Chen Y A,Lu C Y,Shu R,Peng C Z,Wang J Y,Pan J W 2017Science356 1140

[55]Yin H L,Chen T Y,Yu Z W,Liu H,You L X,Zhou Y H,Chen S J,Mao Y Q,Huang M Q,Zhang W J,Chen H,Li M J,Nolan D,Zhou F,Jiang X,Wang Z,Zhang Q,Wang X B,Pan J W 2016Phys.Rev.Lett.117 190501

[56]Bouwmeester D,Pan J W,Mattle K,Eibl M,Weinfurter H,Zeilinger A 1997Nature390 575

[57]Boschi D,Branca S,de Martini F,Hardy L,Popescu S 1998Phys.Rev.Lett.80 1121

[58]Furusawa A,Sorensen J L,Braunstein S L,Funchs C A,Kimble H 1998Science282 706

[59]Nielsen M A,Knill E,La flamme R 1998Nature396 52

[60]Marcikic I,de Riedmatten H,Tittel W 2003Nature421 509

[61]Barren M D,Chiaverini J,Schaetz T,Britton J,Itano W M,Jost J D,Knill E,Langer C,Leibfried D,Ozeri R,Wineland D J 2004Nature429 737

[62]Riebe M,Haffner H,Roos C F,Hänsel W,Benhelm J,Lancaster G P T,Körber T W,Becher C,Schmidt-Kaler F,James D F V,Blatt R 2004Nature429 734

[63]Ma X S,Herbst T,Scheidl T,Wang D Q,Kropatschek S,Naylor W,Wittmann B,Mech A,Ko fler J,Anisimova E,Makarov V,Jennewein T,Ursin R,Zeilinger A 2012Nature489 269

[64]Yin J,Ren J G,Lu H,Cao Y,Yong H L,Wu Y P,Liu C,Liao S K,Zhou F,Jiang Y,Cai X D,Xu P,Pan G S,Jia J J,Huang Y M,Yin H,Wang J Y,Chen Y A,Peng C Z,Pan J W 2012Nature488 185

[65]StevensonR M,NilssonJ,BennettA J,Skiba-Szymanska J,Farrer I,Ritchie D A,Shields A J 2013Nat.Commun.4 2859

[66]Bussieres F,Clausen C,Tiranov A,Korah B,Verma V B,Nam S W,Marsili F,Ferrier A,Goldner P,Herrmann H,Silberhorn C,Sohler W,Afzelius M,Gisin N 2014Nat.Photonics8 775

[67]PfaffW,Hensen B,Bernien H,Dam S B V,Blok M S,Taminiau T H,Tiggelman M J,Schouten R N,Markham M,Twitchen D J,Hanson R 2014Science345 532

[68]Wang X L,Cai X D,Su Z E,Chen M C,Wu D,Li L,Liu N L,Lu C Y,Pan J W 2015Nature518 516

[69]Takesue H,Dyer S D,Stevens M J,Verma V,Mirin R P,Nam S W 2015Optica2 832

[70]Xia X X,Sun Q C 2017J.Inf.Secur.Res.3 36

[71]Duan L M,Lukin M D,Cirac J I,Zoller P 2001Nature414 413

[72]Briegel H J,Dür W,Cirac J I,Zoller P 1998Phys.Rev.Lett.81 5932

[73]Einstein A,Podolsky B,Rosen N 1935Phys.Rev.47 777

[74]Ge H 2014Ph.D.Dissertation(Wuhan:Huazhong University of Science and Technology)(in Chinese)[葛华2014博士学位论文(武汉:华中科技大学)]

[75]Long G L,Wang C,Li Y S,Deng F G 2011Sci.China Phys.Mech.Astron.41 332(in Chinese)[龙桂鲁,王川,李岩松,邓富国2011中国科学:物理力学天文学41 332]

[76]Peng C Z,Yang T,Zhang J,Jin X M,Feng F Y,Yang B,Yang J,Yin J,Zhang Q,Li N,Tian B L,Pan J W 2005Phys.Rev.Lett.94 150501

[77]Salart D,Baas A,Branciard C,Gisin N,Zbinden H 2008Nature405 861

[78]Yin J,Yong H L,Wu Y P,Peng C Z 2011Acta Phys.Sin.60 060307(in Chinese)[印娟,雍海林,吴裕平,彭承志2011物理学报60 060307]

[79]Ursin R,Jennewein T,Ko fler J,Perdigues J,Cacciapuoti L,Matos C J,Aspelmeyer M,Valencia A,Scheidl T,Fedrizzi A,Acin A,Barbieri C,Bianco G,Brukner C,Capmany J,Cova S,Giggenbach D,Leeb W,Hadfield R H,La flamme R,Lütkenhaus N,Milburn G,Peev M,Ralph T,Rarity J,Renner R,Samain E,Solomos N,Tittel W,Torres J P,Toyoshima M,Ortigosa-Blanch A,Pruneri V,Villoresi P,Walmsley I,Weihs G,Weinfurter H,Zukowski M,Zeilinger A 2009Europhys.News40 26

[80]Pfennigbauer M,Aspelmeyer M,Leeb W,Baister G,Dreischer T,Jennewein T,Neckamm G,Perdigues J,Weinfurter H,Zeilinger A 2005J.Opt.Commun.Netw.4 549

[81]Bonato C,Tomaello A,Deppo V D,Naletto G,Villoresi P 2009New J.Phys.11 045017

[82]Chen P,Cai Y X,Cai X F,Shi L H,Yu X T 2015Acta Phys.Sin.64 040301(in Chinese)[陈鹏,蔡有勋,蔡晓菲,施丽慧,余旭涛2015物理学报64 040301]

[83]Vollmer C E,Schulze D,Eberle T,Händchen V,Fiurášek J 2013Phys.Rev.Lett.111 230505

[84]Xu F H,Qi B,Liao Z F,Lo H K 2013Appl.Phys.Lett.103 061101

[85]Cao Y,Liang H,Yin J,Yong H L,Zhou F,Wu Y P,Ren J G,Li Y H,Pan G S,Yang T,Ma X,Peng C Z,Pan J W 2013Opt.Express21 27260

[86]Zhang Y D 2006Principles of Quantum Information Physics(Beijing:Science Press)pp146–154(in Chinese)[张永德 2006量子信息物理原理(北京:科学出版社)第146—154页]

[87]Dong L,Xiao R J,Ren Y P,Xiu X M 2014Quantum Information Transmission over Noisy Channels(Shenyang:Northeastern University Press)pp27–29(in Chinese)[董莉,肖瑞杰,任远鹏,修晓明2014噪声信道中的量子信息传送(沈阳:东北大学出版社)第27—29页]

[88]Wang X B 2005Phys.Rev.A72 050304

[89]Zanardi P,Rasetti M 1997Phys.Rev.Lett.79 3306

[90]Dong L,Xiao R J,Ren Y P,Xiu X M 2014Quantum Information Transmission over Noisy Channels(Shenyang:Northeastern University Press)pp43–54(in Chinese)[董莉,肖瑞杰,任远鹏,修晓明2014噪声信道中的量子信息传送(沈阳:东北大学出版社)第43—54页]

[91]Cirac J I,Zoller P,Kimble H J,Mabuchi H 1997Phys.Rev.Lett.78 3221

[92]Wang Q,Tan M Y,Liu Y,Zeng H S 2009J.Phys.B At.Mol.Opt.Phys.42 125503

[93]Brask J B,Jiang L,Gorshkov A V,Vuletic V,Sørensen A S,Lukin M D 2010Phys.Rev.A81 020303

[94]Sheng Y B,Deng F G 2010Phys.Rev.A81 042332

[95]Salemian S,Mohammadnejad S 2011Chin.Sci.Bull.56 618

[96]Dong L,Xiu X M,Shen H Z,Gao Y J,Yi X X 2013Opt.Commun.308 304

[97]Lin F H 1996Microwave Communication and Satellite Communication(Beijing:Electronic Industry Press)pp1–86(in Chinese)[林福华 1996微波通信与卫星通信(北京:电子工业出版社)第1—86页]

[98]Liu D M,Sun J Q,Lu P 2016Fiber Optics(Beijing:Science Press)p55(in Chinese)[刘德明,孙军强,鲁平2016光纤光学(北京:科学出版社)第55页]

[99]Vernam G S 1926J.Amer.Inst.Elec.Eng.55 109

Quantum communication scheme based on quantum teleportation∗

Yang Lu1)2)Ma Hong-Yang3)Zheng Chao4)Ding Xiao-Lan5)Gao Jian-Cun1)Long Gui-Lu1)6)†

1)(State Key Laboratory of Low-Dimensional Quantum Physics,Department of Physics,Tsinghua University,Beijing 100084,China)
2)(Science and Technology Communication Network Laboratory,Shijiazhuang 050081,China)
3)(School of Sciences,Qingdao Technological University,Qingdao 266033,China)
4)(College of Science,North China University of Technology,Beijing 100144,China)
5)(College of Communication Engineering,Chongqing University,Chongqing 400044,China)
6)(Tsinghua National Laboratory for Information Science and Technology,Beijing 100084,China)

24 April 2017;revised manuscript

24 July 2017)

Quantum communication protects information security by means of the basic laws of quantum mechanics and has aroused the wide public interest over the recent years.Quantum communication consists of quantum key distribution,quantum secure direct communication,quantum teleportation,quantum dense coding,and quantum secret sharing.The purpose of quantum key distribution,quantum secure direct communication and quantum secret sharing is to protect the security of information and thus they are called quantum cryptography.In quantum key distribution and secret sharing,data transmitted in the quantum channel are random keys rather than information,and the information is sent through another classical communication.The direct communication of information through quantum channel is realized in quantum secure direct communication.In this paper,we present a protocol for quantum communication by using quantum teleportation(QCUQT),and analyze it in detail.First,we answer the question whether QCUQT is a type of quantum secure direct communication.In QCUQT,only computational basis states are teleported,and both the Bell-basis measurement and the single particle operations can be simplified.It is found that the QCUQT is equivalent to the combined process of a quantum key distribution plus a classical communication rather than a type of quantum secure direct communication.In order to read out the information in the quantum channel,classical communication is required by QCUQT.Some misunderstandings about QCUQT are discussed and clarified in the paper.It was mistaken that the transmission of quantum state in QCUQT is irrelevant to the channel noise nor the distance between two parties,and QCUQT can even be used to realize superluminal communication.Our study shows that the QCUQT is affected by the medium and also the distance between two parties,and it does not have an advantage over quantum key distribution,and cannot realize quantum superluminal communication either.We also compare the QCUQT with quantum key distribution,quantum secure direct communication,and classical one-time-pad in several aspects such as the nature of the data in quantum channel,the way of reading out the key,the way of transmitting messages,and the amount of data carried in the process.We also point out the characteristics of each type of communication.It is concluded that single-photon quantum key distribution is easier to realize than QCUQT because single-photon detection and generation are easier to realize than the Bell-basis measurement and generation of EPR pairs.In particular,we discuss the use of these protocols in space communication and it is suggested that quantum secure direct communication be a better choice in outer-space quantum communication because of the low loss in quantum channels there.

quantum communication based on quantum teleportation,full-use quantum key distribution,deterministic quantum key distribution,quantum secure direct communication

PACS:03.67.Hk,03.67.Dd,03.65.UdDOI:10.7498/aps.66.230303

*Project supported by the National Natural Science Foundation of China(Grant Nos.91221205,11405093,11547035),the National Basic Research Program of China(Grant No.2015CB921002),and the Scientific Research Starting Foundation of North China University of Technology.

†Corresponding author.E-mail:gllong@tsinghua.edu.cn

(2017年4月24日收到;2017年7月24日收到修改稿)

量子保密通信包括量子密钥分发、量子安全直接通信和量子秘密共享等主要形式.在量子密钥分发和秘密共享中,传输的是随机数而不是信息,要再经过一次经典通信才能完成信息的传输.在量子信道直接传输信息的量子通信形式是量子安全直接通信.基于量子隐形传态的量子通信(简称量子隐形传态通信)是否属于量子安全直接通信尚需解释.构造了一个量子隐形传态通信方案,给出了具体的操作步骤.与一般的量子隐形传态不同,量子隐形传态通信所传输的量子态是计算基矢态,大大简化了贝尔基测量和单粒子操作.分析结果表明,量子隐形传态通信等价于包含了全用型量子密钥分发和经典通信的复合过程,不是量子安全直接通信,其传输受到中间介质和距离的影响,所以不比量子密钥分发更有优势.将该方案与量子密钥分发、量子安全直接通信和经典一次性便笺密码方案进行对比,通过几个通信参数的比较给出各个方案的特点,还特别讨论了各方案在空间量子通信方面的特点.

10.7498/aps.66.230303

∗国家自然科学基金(批准号:91221205,11405093,11547035)、国家重点基础研究发展计划(批准号:2015CB921002)和北方工业大学科研启动基金资助的课题.

†通信作者.E-mail:gllong@tsinghua.edu.cn