二维氢原子中的基态奇异特性数值精确对角化法∗

刘褚航 强百强 季育琛 李炜

1)(上海科技大学物质科学与技术学院,上海 201210)

2)(中国科学院上海微系统与信息技术研究所,信息功能材料国家重点实验室,上海 200050)

二维氢原子中的基态奇异特性数值精确对角化法∗

刘褚航1)强百强1)季育琛1)李炜2)†

1)(上海科技大学物质科学与技术学院,上海 201210)

2)(中国科学院上海微系统与信息技术研究所,信息功能材料国家重点实验室,上海 200050)

二维氢原子,离散贝塞尔基函数,Lanczos法

1 引 言

随着计算机技术的发展,数值精确对角化法在现代计算凝聚态物理学中扮演着至关重要的角色[1],尤其是在强关联电子体系的研究领域中,它已成为其他数值计算技术的参照,尽管数值精确对角化法存在着其只能处理较小的物理系统的局限性.另外,可以通过幺正变换改变基函数的选取,以及通过对称性的约束来极大程度地提高计算体系的尺寸[2],比如通过傅里叶变换将实空间中的哈密顿量变换到动量空间[3],从而改变基函数的选取来处理具有平带特性[4−6]的分数拓扑量子态的新奇特性[7−9],以及极大程度地提高数值计算量和所计算体系的尺寸大小[10,11].

通过幺正变换改变基函数的选取在量子力学中被称为表象变换[12,13].选择合适的表象会让人们对物理系统的图像有更清晰的认识,比如对于自由运动的粒子,在动量表象下它的本征能谱是对角化的;对于超导体中的电子Copper配对,在Bogoliubov表象下它的本征能谱也是对角化的[14].

在本文中,我们利用表象变换选取合适的贝塞尔函数为基函数,再利用Lanczos技术[15]数值精确对角化处理在维度受限下的二维氢原子基态的奇异行为,得到的数值基态波函数与解析结果完全符合.构造这套具有正交性、归一化、完备的离散贝塞尔基函数,将有助于今后研究一些波函数具有数值奇异特性的体系中发挥重要作用;同时,与这套离散贝塞尔基函数相类似的线性缀加平面波的基函数,在基于密度泛函理论框架下的第一性原理计算模拟中也扮演着重要的角色[16,17].

本文讨论了利用解析和数值有限差分法计算三维氢原子的本征能级及其相应的本征波函数,所得到的解析结果与数值结果相一致.这说明数值有限差分法在三维氢原子体系中的合理适用性.同时,进一步推广数值有限差分法到维度受限下的二维氢原子体系,计算发现对于基态波函数所得的解析结果与数值结果不一致,但是对于其他激发态的径向波函数解析和数值计算所得的结果却相一致.这说明二维氢原子体系的基态波函数存在着数值奇异特性.该奇异特性主要体现在基态的径向波函数R(r)随着r趋于0时,简化的径向波函数将趋于有限值,而不再是0.为了在数值上克服该奇异特性,引入一套新的具有轴向对称性的离散贝塞尔基函数,并将径向波函数R(r)用这套新的离散贝塞尔基函数做线性展开,同时利用数值Lanczos技术精确对角化获得了体系基态能量与基态波函数,与解析结果完全一致.

2 三维氢原子模型的解析和数值有限差分法求解

2.1 模型解析求解

对于三维氢原子的定态薛定谔方程可表示为[13]

其中ħ为约化普朗克常数,µ为折合质量,V(r)=−e2/r为三维氢原子的中心势能,E为体系的本征能量,其相应的本征波函数为Ψ(r).考虑到体系的库仑能具有中心球对称性,可以将本征波函数Ψ(r)用球谐函数Ylm(θ,φ)为基做线性展开[18],即

其中R(r)为展开系数,称之为径向波函数,代入到定态薛定谔方程(1),于是得到关于在三维氢原子的中心势场下的径向波函数R(r)所满足的微分方程为

其中l=0,1,2,···称为轨道角动量量子数.引入函数变量代换R(r)=u(r)/r,并代入到微分方程(3),化简得到关于u(r)的微分方程为

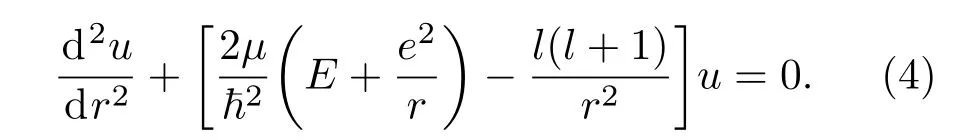
可以较为容易地通过幂级数展开法[19]严格解析求得径向波函数Rnl(r)的解析表达形式及其相对应的本征能量这里n称为主量子数.在l=0时,前三个本征态的径向波函数Rnl(r)的解析形式分别为:

2.2 数值有限差分法

采用数值计算方法来求解径向波函数u(r)所满足的微分方程(4),即利用数值离散差分法化简微分方程(4),并得到差分方程[20]为

图1 三维氢原子径向波函数 (a)u(r)和(b)R(r)的解析(实线)和数值有限差分法(虚线)所得到的结果Fig.1.Radial wave function of the three-dimensional hydrogen atom for u(r)in(a)and R(r)in(b)by using an analytical(solid line)and numerical(dashed line)methods.

其中Δr为离散化的两个格点之间的距离.为求解差分方程(8),首要考虑的是边界条件.考虑到径向波函数u(r)随着r趋于+∞时,径向波函数u(r)将趋于0,以及径向波函数u(r)随着r趋于0时,径向波函数u(r)也将趋于0;同时,结合差分方程(8),可很容易通过数值精确对角化法精确地求解差分方程(8),并得到体系的本征能量及其相应的本征波函数.从图1可以很清楚地看到,对于三维氢原子的径向波函数u(r)和R(r)的解析结果与数值有限差分法所得的结果完全符合,相应的本征能量也完全符合,即解析和数值解得的基态能量均为E1=−13.625 eV.

3 二维氢原子模型的解析和数值有限差分法求解

3.1 模型解析求解

下面讨论二维氢原子情况,即在维度受限下的二维氢原子的定态薛定谔方程可表示为

其中势能V(r)=−e2/r,它已不再具有三维球对称性,而是具有平面轴对称性[18].因此,可以将波函数Ψ(r)用轴向波函数eimθ为基做线性展开,即

其中m=0,±1,±2,···称为磁量子数,它是角动量l在z方向上的投影算符lz的本征值,即算符lz的本征方程为

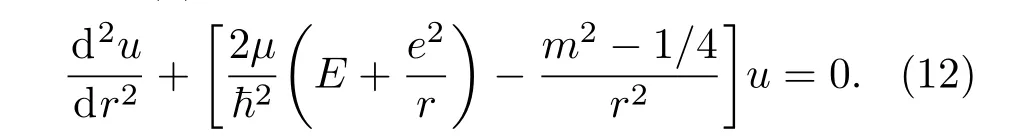
相比三维氢原子的径向波函数u(r)所满足的微分方程(4)而言,可以很清楚地看到两者微分方程的形式是极为相似的,但是对于基态所满足的微分方程,即l=0的三维氢原子和m=0的二维氢原子的微分方程却有着本质的区别,它将会给二维氢原子的基态行为带来诸多奇异性质.

同样地,类似于三维氢原子的幂级数展开解法[19]也很容易地通过幂级数展开法解析求得二维氢原子的径向波函数Rnm(r)的解析表达形式及其相对应的本征能级

3.2 数值有限差分法

采用数值有限差分法数值求解二维氢原子的径向波函数u(r)所满足的微分方程(12)式,并得到离散差分方程[20]为

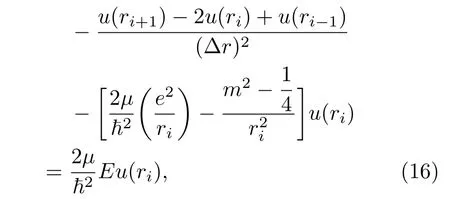
其中Δr为离散化的两个格点之间的距离.为求解差分方程(16),同样需要考虑体系的边界条件.如果依然假设径向波函数u(r)随着r趋于+∞时,径向波函数u(r)将趋于0,以及径向波函数u(r)随着r趋于0时,径向波函数u(r)也将趋于0;同时,结合差分方程(16),可很容易地通过数值精确对角化法求解差分方程(16)并得到体系的本征能量及其相对应的本征波函数.如图2所示,体系在m/=0时的激发态径向波函数unm(r)的解析结果均与数值有限差分法所获得的结果完全符合,但是对于基态径向波函数u10(r),数值有限差分法的结果与解析结果却不一致,同时其相应的本征能量也不一致,即解析解得的基态本征能量为E1=−54.4 eV,而数值有限差分法所解得的基态本征能量为E1=−2214.6 eV.这说明数值有限差分法已不再适用于处理二维氢原子的基态本征值问题.其原因是对于二维氢原子的基态径向波函数u10(r),随着r趋于0时,u10(r)趋于有限值,而不再是零,它与三维氢原子的情形截然不同.出现这样的问题,本质上是源于有限差分方法在处理边界条件问题上存在着局限性,即无法处理具有非零特性的第一类边界条件的微分方程.因此,需要寻找其他数值技术来克服这类问题,比如可以采用贝塞尔函数为基函数做线性展开进行处理[19].

图2 二维氢原子径向波函数 (a)u(r)和(b)R(r)的解析(实线)和数值有限差分法(虚线)所得到的结果Fig.2.Radial wave function of the two-dimensional hydrogen atom for u(r)in(a)and R(r)in(b)by using an analytical(solid line)and numerical(dashed line)methods.

4 以贝塞尔函数为基函数做线性展开的数值精确对角化法

4.1 讨论二维氢原子的径向波函数u(r)在r=0处的渐近行为

以上数值有限差分法的计算结果表明,对于有限差分法已不再适用于处理具有数值奇异特性的二维氢原子体系的基态波函数行为,即本征波函数u10(r)的特征.因此,可以采用另一套数值方法,即将本征波函数用一套具有正交完备性的函数为基函数做线性展开,以此来数值求解此体系的微分方程.考虑到二维氢原子系统具有轴向对称性,可以选用贝塞尔函数为基函数[19].由于贝塞尔函数种类很多,可根据体系的渐近行为,选择一套合适的正交基.首先讨论球贝塞尔函数,它的正交性为[19]

其中α为球贝塞尔函数的阶,uα,m为α阶的球贝塞尔函数的第m个零点.根据基函数的正交特性,可以得到一套正交基为:另外,根据前面的解析计算可知,当m=0时,二维氢原子的径向波函数R(r)在r=0处是一个不为零的有限值.因此,径向波函数u(r)在r=0处的渐近行为必须满足形式.如果这里选用以球贝塞尔函数为正交完备基,那么径向波函数u(r)在r=0处的渐近行为将与r相同,这会导致所计算出来的径向波函数R(0)=0,依然与解析计算结果不一致.因此,当且仅当正交基函数在r=0处的渐近行为满足形式时,径向波函数R(0)的行为才符合解析结果的特性.能满足这种特性的是贝塞尔函数.如果我们考虑贝塞尔函数的连续正交基,其正交关系为[19]

它的积分区间为无穷大,而且还是具有连续变化的基函数,它将不利于数值计算.因此,改用贝塞尔函数的离散正交基,其正交关系为[19]

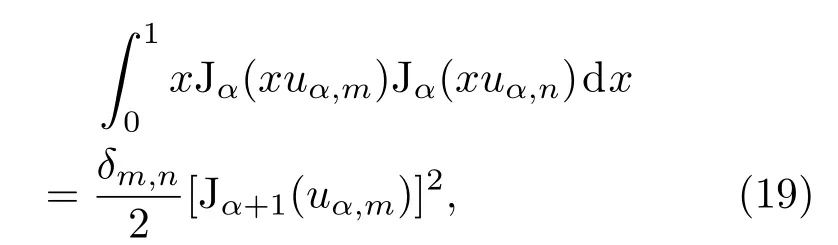
其中α为贝塞尔函数的阶,uα,m为α阶贝塞尔函数的第m个零点.根据正交关系,可很容易地得到一套新的正交完备基为若取α=0,即若选取零阶贝塞尔函数为离散正交基,那么在r=0处,径向波函数R(r)的渐近行为刚好符合形式.

4.2 基于Lanczos技术的数值精确对角化法

根据上述讨论的径向波函数的渐近行为,可以将零阶贝塞尔函数的离散正交基表示为fm:

然后进行变量代换x=y/b,则新的基函数在区间[0,b]上满足正交性,适合于数值求解.通过基的幺正变换后,得到体系的哈密顿量在基函数hm下的矩阵元为

可以通过Lanczos方法[15]数值精确对角化体系的哈密度量H的矩阵元(21)式并得到在基函数hm下的本征矢量v及其相应的本征能量.最终求得二维氢原子的径向波函数u(r)为

在数值计算过程中,选取有限个hi(i=1,2,···,N)作为假想的完备性基函数,其中N为基函数的截断值.理论上,随着选取的截断值N趋于无穷大,基函数hi接近于完备性.但是在实际的数值计算过程中需要对N做截断.截断的合理性根据误差ΔE来确定,即ΔE=En1−Ea1,其中En1表示为数值精确对角化求得的基态能量,而Ea1则表示为解析求得的基态能量.如图3(a)所示,可以清楚地看到随着截断值N的增大,误差ΔE将快速地趋于零.当N=7000时误差已经小于0.005.同时,在N=7000时,还计算了体系的径向波函数u10(r)和R10(r),如图3(b)所示,与解析结果完全一致.

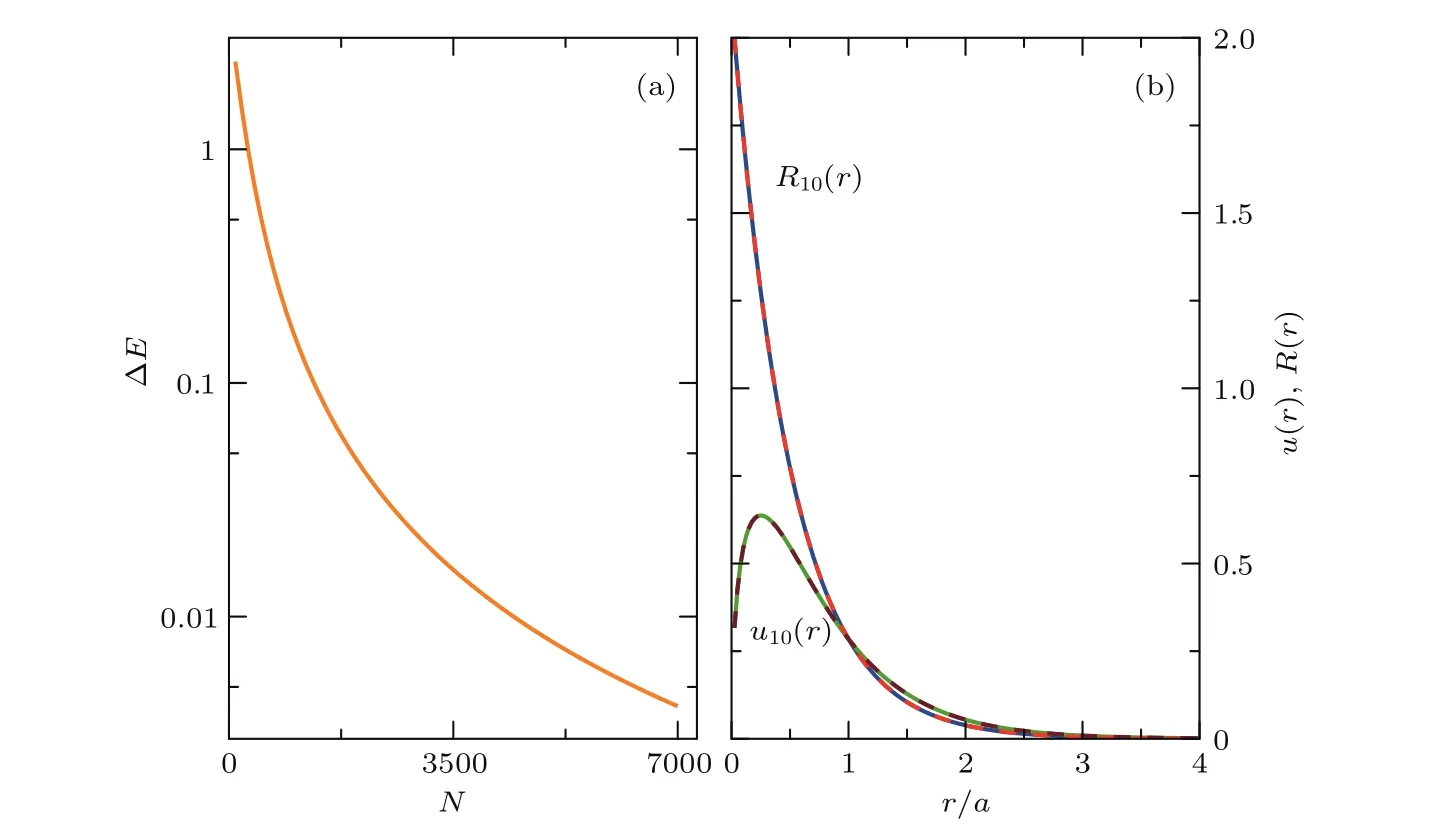
图3 (a)数值计算的基态本征值与理论值之间的误差随基函数个数的关系;(b)基态径向波函数u(r)和R(r)的解析(实线)与数值有限差分法(虚线)所得到的结果Fig.3.(a)Error ΔE between numeral(En0)and analytical(Ea0)results for the ground state of twodimensional hydrogen system;(b)radial wave function of the two-dimensional hydrogen atom for u(r)and R(r)by using an analytical(solid line)and numerical(dashed line)methods for the ground state.

5 结 论

讨论了利用解析和数值有限差分法分别计算三维氢原子和二维氢原子的本征能级及其相应的本征波函数,计算发现由于在维度受限下的二维氢原子体系的基态波函数存在着数值奇异特性.为了解决该数值奇异性,构造了一套新的离散的贝塞尔函数为基函数做线性展开,同时结合数值Lanczos精确对角化法,最终获得体系基态能量和基态波函数均与解析相一致的结果.这套新的完备的离散贝塞尔基函数的构造可以在研究一些波函数具有数值奇异特性的体系中发挥至关重要的作用.

[1]Fehske H,Schneider R,Weibe A 2008Computational Many-Particle Physics(Berlin:Springer)p529

[2]Lin H Q 1990Phys.Rev.B42 6561

[3]Regnault N,Bernevig B A 2011Phys.Rev.X1 021014

[4]Tang E,Mei J W,Wen X G 2011Phys.Rev.Lett.106 236802

[5]Sun K,Gu Z C,Katsura H,Sarma S D 2011Phys.Rev.Lett.106 236803

[6]Neupert T,Santos L,Chamon C,Mudry C 2011Phys.Rev.Lett.106 236804

[7]Sheng D N,Gu Z C,Sun K,Sheng L 2011Nat.Commun.2 389

[8]Li W,Liu Z,Wu Y S,Chen Y 2014Phys.Rev.B89 125411

[9]Li W,Sheng D N,Ting C S,Chen Y 2014Phys.Rev.B90 081102(R)

[10]Li W,Chen Y 2016EPL113 47001

[11]Liu C R,Guo Y W,Li Z J,Li W,Chen Y 2016Sci.Reports6 33472

[12]Dirac P A M 1982The Principles of Quantum Mechanics(Oxford:Oxford Science Publications)p53

[13]Shankar R 1994Principles of Quantum Mechanics(New York Plenum Press)p115

[14]Bardeen J,Cooper L,Schriffer J R 1957Phys.Rev.8 1178

[15]Lanczos C 1950J.Res.Nat.I Bur.Std.45 255

[16]Hohenberg P,Kohn W 1964Phys.Rev.136 B864

[17]Singh D 1994Planewaves,Pseudopotentials and the LAPWMethod(Boston/Dordecht/London: Kluwer Academic Publishers)p43

[18]Dresselhaus M S,Dresselhaus G,Jorio A 2008Group Theory Application to the Physics of Condensed Matter(Springer)p57

[19]Wang Z X,Guo D R 2012Introduction to the Special Functions(Beijing:Peking University Press)p381(in Chinese)[王竹溪,郭敦仁 2012特殊函数概论 (北京:北京大学出版社)第381页]

[20]Ma W T 2016Computational Physics(Beijing:Science Press)p64(in Chinese)[马文淦 2016计算物理学 (北京:科学出版社)第64页]

Numerical exact diagonalization of singularity in the ground state of two-dimensional hydrogen atom∗

Liu Chu-Hang1)Qiang Bai-Qiang1)Ji Yu-Chen1)Li Wei2)†

1)(School of Physical Science and Technology,ShanghaiTech University,Shanghai 201210,China)
2)(State Key Laboratory of Functional Materials for Informatics,Shanghai Institute of Microsystem and Information Technology,Chinese Academy of Sciences,Shanghai 200050,China)

6 July 2017;revised manuscript

13 August 2017)

With the development of computing technology,numerical exact diagonalization method plays a vital role in modern computational condensed matter physics,especially in the research area of strongly correlated electron systems:it becomes a benchmark for other numerical computational techniques,such as quantum Monte Carlo,numerical renormalization group,density matrix renormalization group,and dynamic mean field theory.In this paper,we first numerically exactly diagonalize the three-dimensional hydrogen atom with the combination of finite-difference method,and find that the numerical wave function of ground state is in good agreement with the analytical calculations.We then turn to discuss the space dimension confinement hydrogen system,two-dimensional hydrogen atom,and notice that the numerical wave function is no longer in agreement with the analytical calculation,where the ground state wave function has a numerical singularity as radius approaches to zero.Compared with the case of the three-dimensional hydrogen atom,this issue mainly comes from the nature of space dimension confinement.To resolve such an issue of numerical singularity in two-dimensional hydrogen atom,we need to construct a new discrete and normalized Bessel function as a basis to study the ground state behavior of dimension confinement system based on the framework of Lanczos-type numerical exact diagonalization.The constructed normalized Bessel basis is orthogonal and discrete,and thus becomes suitable for practical calculation.Besides,these prominent properties of such a Bessel basis greatly reduce the complexity and difficulty in practical calculation,and thus makes computing work efficient.In addition,Lanczos-type numerical exact diagonalization method can extremely speed up the process of solving the eigenvalue equation.As a result,such a high efficient calculation of our method demonstrates the consistence between numerical and analytical ground state energy value,and the corresponding wave function with enough truncated basis number.Since this kind of numerical singularity occurs in many space dimension confinement systems,our finding for constructing a new discrete Bessel basis function may be helpful in studying the quantum systems with numerical singularity behaviors in wavefunctions in future.On the other hand,it should be pointed out that the Bessel basis is incorporated into the linear augment plane wave method in the density functional theory to study the electronic band structure of the condensed material and obtain high accurate results,especially in the theoretical prediction of topological insulators and in experimental realization as well.

two-dimensional hydrogen atom,discrete Bessel basis function,Lanczos-type numerical exact diagonalization

PACS:01.40.Fk,03.65.Ge,03.67.LxDOI:10.7498/aps.66.230102

*Project supported by the National Natural Science Foundation of China(Grant No.11404359)and the Youth Innovation Promotion Association of the Chinese Academy of Sciences(Grant No.2016215).

†Corresponding author.E-mail:liweiphysics@gmail.com

(2017年7月6日收到;2017年8月13日收到修改稿)

利用数值有限差分法处理二维氢原子的基态波函数时,计算结果发现其存在着数值奇异特性.本文通过构造一套具有正交完备性的离散贝塞尔基函数,并结合基于Lanczos技术的数值精确对角化方法研究二维氢原子中的基态波函数的数值奇异特性,得到的波函数数值解及其相应的本征能量均与解析结果相一致.这套新的完备的离散贝塞尔基函数,可以在研究一些波函数具有数值奇异特性的体系中发挥至关重要的作用.

10.7498/aps.66.230102

∗国家自然科学基金(批准号:11404359)和中国科学院青年创新促进会计划(批准号:2016215)资助的课题.

†通信作者.E-mail:liweiphysics@gmail.com