结合可视图的多状态交通流时间序列特性分析∗

邢雪 于德新 田秀娟 王世广

1)(吉林大学交通学院,长春 130022)

2)(吉林化工学院信息与控制工程学院,吉林 132022)

3)(吉林大学吉林省道路交通重点实验室,长春 130022)

结合可视图的多状态交通流时间序列特性分析∗

邢雪1)2)†于德新1)3)田秀娟1)王世广1)

1)(吉林大学交通学院,长春 130022)

2)(吉林化工学院信息与控制工程学院,吉林 132022)

3)(吉林大学吉林省道路交通重点实验室,长春 130022)

交通流时间序列,可视图,复杂网络,聚类分析

1 引 言

交通流运行状态随人、车、路和环境等多要素变化,交通流时间序列呈现非线性特征和随机特性[1].对于交通流时间序列的分析主要采用随机过程理论、数理统计学方法[2]和机器学习方法(如聚类法、支持向量机)等[3,4],结合交通理论[5]进行动态特征分析.近年来,复杂网络理论在时间序列动态特征分析中的使用引起了极大关注[6−8],已经有相应的研究应用于不同领域的时间序列分析中[9].研究表明用复杂网络分析动态系统是可行的,这为交通流序列提供了可视化分析的途径[10].

由于交通状态的不同会影响其时间序列的幅度变化范围,为此首先建立交通流主要变量(交通流量、占有率和地点平均速度)之间的实际关联关系,利用K-medoids方法进行交通流状态分类,然后通过可视图理论构建多状态交通流时间序列复杂网络,分析比较其对应网络的特征,如度分布、聚类系数、网络直径、模块化,比较不同交通流状态下交通流时间序列的统计规律.

2 基于K-medoids方法的交通流状态分类

为分析交通流时间序列的特征,研究实际数据发现交通状态不同对交通流参量时间序列幅度变化有相应的影响.考虑到这种影响,首先利用聚类分析方法对交通流进行分类.选用K-medoids算法进行交通状态的聚类分析.K-medoids算法具有算法简单、收敛速度快及局部搜索能力强等优点,已应用于很多领域[11−13].

实验数据源采用2015年1月24日厦门市某路段实时检测的1440条交通数据(每条数据包括实时交通流量、占有率和地点平均速度),交通参量采集时间单位为1 min.根据宏观基本图理论,不同交通状态下的交通流量、占有率和速度之间存在关联.为了进一步探讨不同交通流状态下交通流时间序列的特征,根据《城市道路交通拥堵评价指标体系》中给出的道路拥堵等级将数据分为5级(拥堵程度分为非常畅通、畅通、轻度拥堵、中度拥堵和严重拥堵).采用K-medoids方法对输入样本进行分类,向量xi=(xi1,xi2,···,xij),i=1,2,3,其中j表示样本数据的数量,x1j表示时间占有率,x2j表示路段交通流量,x3j表示区域平均速度.从数据集中选出平方差最小的k个聚类中心,并将数据集划分为k个聚类(实验中选取k=5).

交通流状态的K-medoids方法分类主要流程如下:从1440个对象的数据集中随机选择k个样本(k=5)作为初始中心点;将剩余的样本指派给距其最近的中心点所代表的簇;计算平方差函数w(l),

式中p为类Lj中的样本,oi为聚类中心,按照平方差函数值减小的方向,更新每个簇的中心点,重复执行直到聚类不再发生变化.

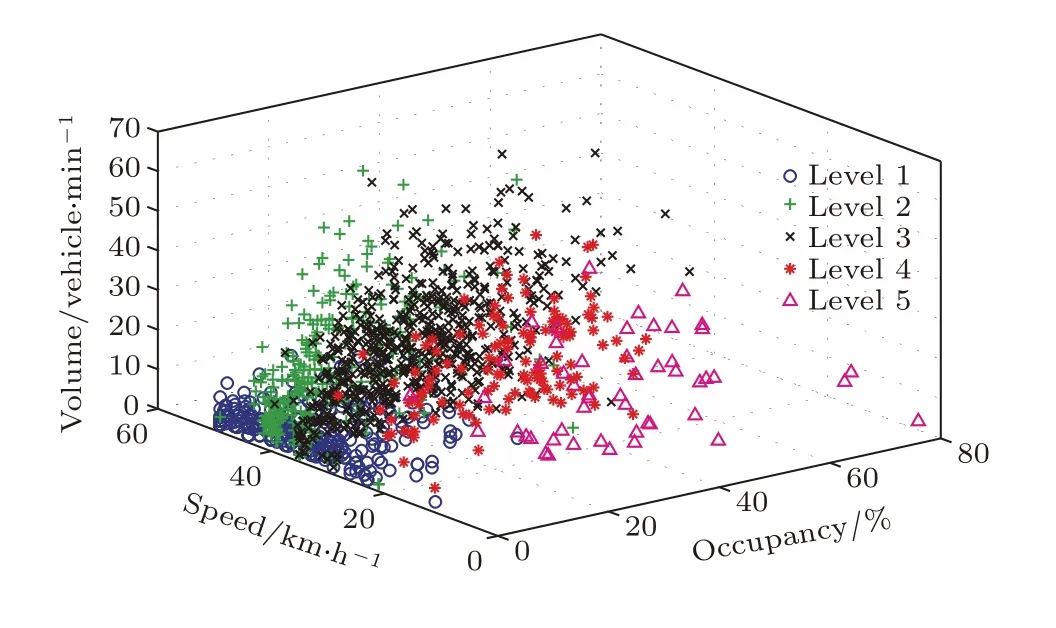
图1 基于K-medoids方法的交通流状态分类三维数散点图Fig.1.Scatter plot of traffic state classi fication based on K-medoids.

图3 三个交通参量在不同交通状态下的提取图 (a)时间占有率的时间序列曲线;(b)交通流量的时间序列曲线;(c)区域平均速度的时间序列曲线Fig.3.Extraction figures of three traffic parameters in different states:(a)Time series of time occupancy;(b)time series of traffic flow;(c)time series of speed.

实验样本数据点分类结果如图1所示,图中数据点以实时交通流量、占有率和地点平均速度为坐标确定样本点位置,1—5级表示交通流的等级划分,1级表示交通运行最畅通,5级表示交通运行最拥堵.为清晰表示不同交通流状态下变量之间的关系,根据宏观基本图理论构建任意两个交通流变量之间的关系模型,并进行数据拟合.图2(a)所示为时间占有率与交通流量之间的相互关系及基于时间占有率增长的交通流量散点拟合曲线;图2(b)为时间占有率与区域平均速度之间的相互关系及基于时间占有率增长的平均速度散点拟合曲线;图2(c)为区域平均速度与交通流量之间的相互关系及基于区域平均速度增长的交通流量散点拟合曲线.在图2(a)中,数据拟合线方程为Q=−0.0234T2+1.4979T+6.5924,其中T为时间占有率,Q为交通流量,三个估计参数的置信区间为[−0.02399,−0.02281],[1.46934,1.52045]和[6.22742,6.95738]. 在图2(b)中,数据拟合线方程为V=−0.0334T+33.9681,其中V为区域平均速度,两个估计参数的置信区间为[−0.03516,−0.03164]和[33.58776,34.34844]. 在图2(c)中,数据拟合线方程为Q=−0.0281V2+1.5126V+1.2703,三个估计参数的置信区间 为[−0.03354,−0.02265],[1.11743,1.90776]和[0.46310,2.07749].上述估计均为95%置信度.

图3为提取5个级别状态划分中三个交通变量的时间序列图.在图3中,I1,I2,I3,I4和I5表示从数据样本向量中分别提取5个级别交通状态下时间占有率的时间序列,II1,II2,II3,II4和II5表示从数据样本向量中分别提取5个级别交通状态下交通流量的时间序列,III1,III2,III3,III4和III5表示从数据样本向量中分别提取5个级别交通状态下区域平均速度的时间序列.I1,II1,III1均表示1级状态下的交通非常畅通,从中可以发现交通流量与时间占有率变化较大,区域平均速度在5个级别状态中波动最大,表明实际情况中车辆的数量不稳定且车辆行驶自由度较高.I2,II2,III2均表示2级状态下的交通畅通,从中可以发现交通流量与时间占有率变化自由度同1级相比幅度有所减小,交通参量的数值明显增大,区域平均速度保持平稳且数值较高,说明实际情况中车辆的数量增多且车辆行驶状态趋于稳定.I3,II3,III3均表示3级状态下的交通轻度拥堵,此状态特点为持续时间长且所有变量的值相对稳定,交通流量与时间占有率持续保持在较高水平,区域平均速度长时间保持平稳,表明在实际情况中车辆的数量继续增多且车辆行驶状态保持稳定.I4,II4,III4均表示4级状态下的交通中度拥堵,从中可以发现交通流量与时间占有率变化幅度与3级相似,区域平均速度明显下降,表明实际情况中车辆行驶受阻且道路负荷呈现饱和态.I5,II5,III5均表示5级状态下的交通严重拥堵,从中可以发现交通流量与时间占有率保持相反变化状态,时间占有率明显上升而交通流量降至较低水平,区域平均速度明显下降,表明在实际情况中车辆行驶受阻严重且道路呈现过饱和态.

3 交通流时间序列的复杂网络构建

时间序列的复杂网络构建方法主要有可视图法[14,15]、周期时间序列构建法[16,17]和相空间重建法[18].其中后两种方法的机理是基于时间序列的相关系数,所以必须估计临界阈值[19−21].实际获取的交通流时间序列不满足周期时间序列的分析要求,不适用周期时间序列构建法.而相空间重建法对于嵌入维度和时间窗参数的依赖性强.综合考虑后利用可视图法构建针对交通流时间序列的复杂网络,利用复杂网络的表象重新认识交通流时间序列,以复杂网络的分析方法来分析交通流时间序列的规律.

可视图法是一种将时间序列映射到网络的快捷方法,算法主要借助构建复杂网络来表征时间序列的网络结构,对交通流(相关三个交通参量)构建复杂网络的流程如图4所示,其中若时间序列中的两个任意数据值(ta,y(ta))和(tb,y(tb))之间的任何(ti,y(ti))(ta＜ti＜tb),使得成立,则这两个数据值(ta,y(ta))和(tb,y(tb))所构成的图节点间关联是可见的.

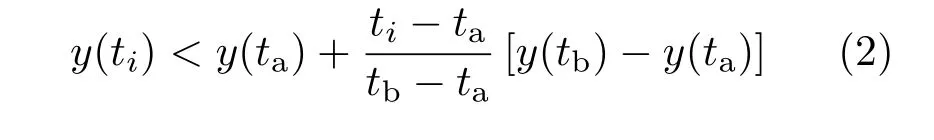
图4 交通流时间序列的复杂网络构建流程Fig.4.Construction process of complex network of traffic flow time series.

通过每一类交通状态中三个交通参量时间序列的柱状图,分析每一类交通状态下交通参量对应网络的邻接矩阵.对每个交通状态分类下三个交通参量时间序列的三个邻接矩阵进行矩阵叠加,使得矩阵可以最大化反映交通流时间序列的关联特征.由于每个矩阵都是布尔矩阵,所以每一类交通状态对应网络的邻接矩阵为M=MQ∨MT∨MV,即以矩阵表示法得到相应构造的复杂网络.

4 交通流时间序列网络特征分析

4.1 交通流时间序列的复杂网络结构

结合上述方法,构建了基于多种交通状态的交通流时间序列网络,相应每类交通状态网络的矩阵图表示如图5所示,形成的网络结构如图6所示.图5(a)—图5(e)分别为5个级别交通流状态的交通流时间序列网络矩阵图,图6(a)—图6(e)分别为5个级别交通流状态的交通流时间序列网络使用Gephi软件绘制的网络结构图.

图5 不同交通状态构建网络的交通流时间序列矩阵图 (a)1级;(b)2级;(c)3级;(d)4级;(e)5级Fig.5.Matrix of traffic time series for different traffic state networks:(a)Level 1;(b)level 2;(c)level 3;(d)level 4;(e)level 5.

图6 (网刊彩色)基于不同交通状态的交通流时间序列复杂网络图 (a)1级;(b)2级;(c)3级;(d)4级;(e)5级Fig.6.(color online)Complex network diagram of traffic time series based on different states:(a)Level 1;(b)level 2;(c)level 3;(d)level 4;(e)level 5.

利用可视图方法构建的网络邻接矩阵有如下特征.在交通非常畅通的状态下,交通流中各参量时间序列的变化均较大且车流自由度较大(如图3中I1,II1和III1所示),反映在矩阵(即体现可见的边)中着色点分布呈现分散状,即沿着对角线方向重叠的大方形,如图5(a)所示.同样在可见图中映射出的边与节点分布较均匀,仅在个别节点处(对应时间序列的结束阶段)显现出可见边密集的情况,如图6(a)所示.这表明在交通非常畅通的状态下,网络呈现均匀分布状态.在交通畅通的状态下,交通流中各参量时间序列的变化幅度趋缓(如图3中I2,II2和III2所示),反映在矩阵中着色点分布呈现沿对角线方向成型的小方形,如图5(b)所示;同样在可见图中映射出的边与节点分布中出现集聚的特征,即出现彼此紧密连接的节点,如图6(b)所示,这表示对应的原时间序列中的数据点相关性较高,且其矩阵中对应方形越小网络的集聚特征越明显.在交通轻度拥堵的状态下,交通流中各参量时间序列处于稳定状态,在各个交通参量时间序列中均没有明显的波动点,且此状态持续时间在整个采集时间中所占比例最大(如图3中I3,II3和III3所示),对应图5中最大的矩阵分布.由于矩阵较大,因而体现反映状态的表象特征比例略小,但依然可判断出着色点分布呈现成型的小方形且这些方形分布密集,如图5(c)所示;同样在可见图中出现非常明显的集聚特征,如图6(c)所示,交通状态从非常畅通到畅通,再从畅通到轻度拥堵的状态变化过程中,网络中的集聚群落数量逐渐增多,可视图中集聚群落特征也呈现得更加明显,由此网络的集聚群落特征可充分映射与交通流时间序列的关联特性.在交通中度拥堵状态下,道路负荷呈现饱和状态,交通流中各参量时间序列依旧保持平稳,未呈现大幅度波动,但区域平均速度明显下降(如图3中I4,II4和III4所示),时间序列的局部峰值被映射到周边邻近的点,在矩阵中呈现沿对角线方向成型的小方形且同比可见边增多,如图5(d)所示;同样在可见图中映射具有集聚特征的网络结构,但由于网络对应映射的时间序列点较少,可见图中特征不显著,如图6(d)所示.在交通严重拥堵状态下,交通参量中交通流量与时间占有率时间序列呈现反向变化趋势,且呈现较大幅度的波动(如图3中I5,II5和III5所示),因而在多个交通参量时间序列的复合矩阵中反映出相同的沿对角线方向形态明显的方形,如图5(e)所示;由于图6(e)中网络对应映射的时间序列点偏少,可见图中特征不显著.上述分析表明,交通状态从非常畅通到中度拥堵的过程中,网络群落数目迅速增长;交通状态从中度拥堵到严重拥堵的过程中,网络群落数目缓慢减少.

4.2 交通流时间序列的复杂网络特征

通过统计网络的度分布、聚类系数、网络直径、模块化等描述和分析网络特征,并进一步研究网络的动力学特征.研究分析了实例中构造的不同交通状态时间序列网络的聚类系数、网络直径、模块化、图密度和平均路径长度等统计特征,如表1所示.表中比较不同状态交通流时间序列网络的统计特征,表现为网络直径基本保持同一水平.网络的聚类系数和模块化应结合时间序列可视化特性分析,表现为交通状态变化越趋近于中度拥堵,网络结构模块化越高.由于交通状态的网络时间序列点数目不同,当序列点数量变少时模块化呈现不足,而将整体考虑为一个模块,表现为体现整体关联的聚类系数增大,同样符合交通状态越拥堵、网络结构模块化(在小网络结构中表现为聚类系数)越高的特点.

构建的5个网络的节点度分布散点及拟合曲线如图7所示,其中度分布分别对应图6(a)—图6(e)的交通流时间序列网络度分布.图7中对应图6(a)网络的散点拟合符合幂律分布,数据拟合线方程为y1=9043d−12.143,其中y1表示相同节点度的个数,d1表示图中节点度数,拟合估计参数的置信区间为[−638.9,18720],[−2.522,−1.764].图7中对应图6(b)—图6(e)的散点拟合符合高斯分布,图6(b)网络数据拟合线方程为y2=17.29exp{−[(d2−18.89)/10.02]2},拟合估计参数的置信区间为[14.52,20.05],[17.5,20.27]和[7.851,12.18];图6(c)网络数据拟合线方程为y3=40.75exp{−[(d3−17.64)/8.262]2},拟合估计参数的置信区间为[36.95,44.56],[16.99,18.29]和[7.25,9.273];图6(d)网络数据拟合线方程为y4=8.183exp{−[(d4−18.31)/9.332]2},拟合估计参数的置信区间为[6.687,9.678],[16.87,19.75]和[7.01,11.65];图6(e)网络数据拟合线方程为y5=2.938exp{−[(d5−18.58)/12.72]2},拟合估计参数的置信区间为[2.075,3.801],[15,22.16]和[5.283,20.16].上述估计置信度均为95%.

表1 交通流时间序列的复杂网络统计特征Table 1.Statistical characteristics of complex network with traffic time series.

图7 网络节点度分布图Fig.7.Degree distribution of network.

5 结 论

在考虑现有实例数据对应交通状态差异的基础上,针对K-medoids方法进行交通状态分类后的交通流时间序列,结合可视图算法构建了交通流时间序列的复杂网络.算法对实际路网的实时检测交通数据进行处理,并分析了不同交通状态下交通流时间序列网络的统计特性.

与传统的交通流序列研究方法不同,本研究使用复杂网络作为工具,利用网络分析统计特性的方式来分析交通流的属性,即从可视化的网络角度重新认识交通流:1)衡量交通流状态需要多个参量,而可视图法只能处理单变量时间序列,直接应用可视图法不能体现交通流整体特征,所以采用矩阵叠加的方式构建多参量的交通流时间序列的网络矩阵,为交通流时间序列映射到网络提供了有效方式;2)传统交通流理论通过宏观基本图分析交通流变量之间的相关性,进而对交通状态进行划分,而本研究构建的实例网络发现网络特性(如网络结构的模块化、聚类系数和度分布)在不同状态下具有不同的模式,通过不同的属性模式可以识别不同的交通状态.现阶段初步利用可视图方法分析研究了交通流时间序列的属性,之后将继续探讨其他构建时间序列网络的方法并比较其优缺点,为分析交通流的运行态势提供更多途径.

[1]He Z C,Li Z T,Zhao J M 2010J.Sw.Jiaotong Univ.45 946(in Chinese)[何兆成,黎志涛,赵建明 2010西南交通大学学报45 946]

[2]Dou H L,Liu H D,Wu Z Z,Yang X G 2009J.Tongji Univ.(Natural Science Edition)37 486(in Chinese)[窦慧丽,刘好德,吴志周,杨晓光 2009同济大学学报(自然科学版)37 486]

[3]Xing X,Yu D X,Tian X J,Cheng Z Y 2016J.Huazhong Univ.Sci.Technol.(Natural Science Edition)44 160808(in Chinese)[邢雪,于德新,田秀娟,程泽阳 2016华中科技大学学报(自然科学版)44 160808]

[4]Zhang Y M,Wu X J,Bai S L 2013Acta Phys.Sin.62 190509(in Chinese)[张玉梅,吴晓军,白树林2013物理学报62 190509]

[5]Treiber M,Kesting A,Helbing D 2010Transp.Res.B44 983

[6]Ling X,Hu M B,Jiang R,Wu Q S 2010Phys.Rev.E81 16113

[7]Gao Z K,Jin N D,Yang D,Zhai L S,Du M 2012Acta Phys.Sin.61 120510(in Chinese)[高忠科,金宁德,杨丹,翟路生,杜萌2012物理学报61 120510]

[8]Gao X Y,An H Z,Fang W 2012Acta Phys.Sin.61 098902(in Chinese)[高湘昀,安海忠,方伟2012物理学报61 098902]

[9]Gao Z,Jin N 2012Physica A391 3005

[10]Zhang J,Cao X B,Du W B,Cai K Q 2010Physica A389 3922

[11]Arora P,Deepali D,Varshney S 2016Proc.Comput.Sci.78 507

[12]Madhulatha T 2012Int.Organ.Sci.Res.J.Eng.2 719

[13]Mishra N,Motwani R 2004Mach.Learn.56 35

[14]Lucas L,Bartolo L,Fernando B,Jordi L,Juan C N 2008Proc.Natl.Acad.Sci.105 4972

[15]Lacasa L,Toral R 2010Phys.Rev.E82 36120

[16]Zhang J,Sun J F,Luo X D,Zhang K,Nakamura T,Small M 2008Physica D237 2856

[17]Zhang J,Small M 2006Phys.Rev.Lett.96 238701

[18]Xu X,Zhang J,Small M 2008Proc.Natl.Acad.Sci.105 19601

[19]Donner R V,Zou Y,Donges J F,Marwan N,Kurths J 2010Phys.Rev.E81 15101

[20]Yang Y,Yang H J 2008Physica A387 1381

[21]Tang J,Wang Y,Liu F 2013Physica A392 4192

Analysis of multi-state traffic flow time series properties using visibility graph∗

Xing Xue1)2)†Yu De-Xin1)3)Tian Xiu-Juan1)Wang Shi-Guang1)

1)(College of Transportation,Jilin University,Changchun 130022,China)
2)(College of Information and Control Engineering,Jilin Institute of Chemical Technology,Jilin 132022,China)
3)(Jilin Provincial Key Laboratory of Road Traffic,Jilin University,Changchun 130022,China)

19 March 2017;revised manuscript

23 July 2017)

A traffic flow time series is a sequence of traffic detection parameters in chronological order.This differs from a general quantitative data sequence in that the time series includes a time attribute that contains not only the data with time characteristics,but also the distribution of the data itself.To date,studies of traffic time series have primarily adopted data mining methods consisting of data mining and machine learning methods—similar sequence search,dimension reduction,clustering,classification,pattern analysis,prediction,etc.In order to improve the visualization of traffic flow time series and feature analyses,a proposed method builds the association networks of traffic flow time series by using visibility graph theory.This approach differs from traditional traffic flow theory as it performs feature analysis of traffic flow time series from the perspective of complex networks,and then analyzes the relationship between the characteristics of the structure in the visual network and the state characteristics of the traffic flow.The proposed method also takes into account the different traffic flow time sequences that correspond to different traffic states.

In the network building process using the proposed method,the traffic flow is classified by correlating the traffic flow parameters to the structure of the complex time series networks under different traffic conditions through considering the changes in traffic flow characteristics under various traffic conditions.Next,statistical analyses of the signs and attributes of the networks(e.g.degree distribution,clustering coefficient,network diameter,and modularization)are conducted.The analysis results show that the proposed visibility graph method can provide an effective approach to mapping traffic flow time series to the network.Moreover,the modularity,clustering coefficient,and degree distribution of the traffic flow time series networks in different traffic states show specifically varying patterns,providing a way to visually analyze the trends in traffic flow operation.When the traffic condition is at level 1,the distribution of the scattered points of the network conforms to a power law distribution.When the traffic condition is at any other level,the distribution of the scattered points of the network is consistent with a Gaussian distribution.The modularity of the time series network also shows some statistical characteristics,that is,the number of modules grows rapidly when the traffic state switches from smooth to moderate congestion,but decreases slowly when the traffic state switches from moderate congestion to serious congestion.These characteristics can be used to distinguish different traffic states,providing more perspective to understand different traffic scenarios.In this work we preliminarily study the attributes of traffic time series based on the proposed visibility graph method.Future efforts will continue to compare various methods of time series network construction to determine the pros and cons of each method for further analysis.

traffic flow time series,visibility graph,complex network,cluster

PACS:05.45.Tp,45.70.Vn,89.75.FbDOI:10.7498/aps.66.230501

*Project supported by the National Natural Science Foundation of China(Grant No.51308248)and the National Key Technology Support Program of China(Grant No.2014BAG03B03).

†Corresponding author.E-mail:patricia_xx@126.com

(2017年3月19日收到;2017年7月23日收到修改稿)

交通流时间序列的研究主要采用数据挖掘和机器学习的方法,这些“黑箱”挖掘方法很难直观反映序列特性.为增强交通流时间序列及其特征分析的可视化性,结合可视图理论来构建交通流时间序列的关联网络,从复杂网络角度实现交通流时间序列的特性分析.在网络构建的过程中,考虑到不同交通状态下交通流表征具有的差异性,首先利用交通流参量的相关性对交通流状态进行分类,然后构建不同交通状态下的时间序列复杂网络,并对这些网络的特征属性给出统计分析,如度分布、聚类系数、网络直径、模块化等.研究表明,可视图法可为交通流时间序列映射到网络提供有效途径,并且不同状态下交通流时间序列构建的复杂网络的模块化、聚类系数和度分布等统计特征呈现一定的变化规律,为交通流运行态势的研究提供了可视化的分析角度.

10.7498/aps.66.230501∗国家自然科学基金(批准号:51308248)和国家科技支撑计划(批准号:2014BAG03B03)资助的课题.

†通信作者.E-mail:patricia_xx@126.com