半无限深势阱中自旋相关玻色-爱因斯坦凝聚体的量子反射与干涉∗

赵文静 文灵华

(燕山大学理学院,河北省微结构材料物理重点实验室,秦皇岛 066004)

半无限深势阱中自旋相关玻色-爱因斯坦凝聚体的量子反射与干涉∗

赵文静 文灵华†

(燕山大学理学院,河北省微结构材料物理重点实验室,秦皇岛 066004)

自旋相关玻色-爱因斯坦凝聚体,半无限深势阱,量子反射,量子干涉

1 引 言

物质波的量子反射与干涉是量子物理中最有趣的效应之一.近年来,科学家们先后实现了玻色-爱因斯坦凝聚体(Bose-Einstein condensates,BECs)的干涉[1],以及硅固体表面BECs的量子反射[2,3],引起了实验和理论物理学家的广泛关注.首先,量子反射与干涉过程中形成的干涉条纹是宏观系统量子性和相干性的强有力证据.其次,量子反射与干涉为研究超冷原子气体的多体物理提供了一条重要的途经.借助于BECs的量子干涉与反射,人们揭示了超冷玻色原子气体中的超流-莫特绝缘体相变[4]、低维量子涨落[5]、量子关联[6]和量子排斥[7],时空量子结构的普朗克尺度物理[8],涡旋与反涡旋叠加态[9],物质波的输运、囚禁和动力学激发等[10,11].再者,BECs的量子反射与干涉在设计原子芯片实现冷原子的精确操控方面具有潜在的应用价值,例如可用于反射、输运、分离和重组原子云[12,13].

近来Bloch小组实现了自旋相关光晶格中BECs的分离和相干输运[14],为操纵多体系统的量子态和基于冷原子体系的量子信息处理开辟了一个重要的新渠道.对于该实验中观察到的干涉条纹,常规的相位相干理论(包括标准的相位相干、测量导致的相位相干和相互作用导致的相位相干等)[15−20]、关联函数分析[21,22]和光晶格的周期决定论[23,24]是无效的,这些理论不能解释其干涉图样的形成机理.Wen等[25−27]提出了一个新的理论模型,成功地解释了实验中观测到的干涉条纹,分析了自旋相关光晶格中BECs的干涉机理和物理本质.研究表明,单个原子内部自由度与外部自由度的纠缠是自旋相关光晶格中BECs干涉的充分条件,这类干涉与凝聚体的相位无关,即每一个凝聚体只和它自己发生干涉,任意两个不同的凝聚体之间没有干涉效应.最近,Yue等[28]还研究了临界区域超冷玻色气体的物质波干涉.

对于单组分BECs的量子反射或干涉已有大量的实验和理论研究,但关于多组分BECs体系中并存的量子反射和干涉的研究还少有系列报道.本文研究了半无限深势阱中自旋相关BECs的量子反射与干涉,发现了显著调制的干涉条纹,分析了自旋相关输运距离、自旋态和相对相位对干涉条纹的可见度、条纹间距和密度振荡的影响,对理解自旋相关光晶格中的相干输运性质和BECs的干涉机理有一定帮助,为进一步检验自旋相关光晶格中BECs干涉的理论模型和物理本质提供有价值的参考.

2 理论模型

理论模型基于Bloch小组实验[14]的操作顺序建立.首先,在谐振子磁阱中制备BECs,原子处于超精细能级|F=1,mF=−1〉.然后,叠加三维的光晶格势,其中x方向形成自旋相关光晶格势.通过增加光晶格势垒的高度,系统由超流相进入莫特绝缘相,不再具有长程的相位相干性.最后,绝热关闭磁阱以及y轴和z轴方向的光晶格,从而可以在单粒子水平上对沿x轴方向的自旋相关输运过程本身进行实验研究,无需考虑原子间相互作用导致的多体态相移.详细的实验过程参见文献[14].当磁阱和y轴、z轴方向的光晶格撤除后,有一系列BECs形成于沿x轴方向的一维自旋相关光晶格.由于系统事先经历了莫特相变,不同格点中的BECs彼此之间不具有相干性,相邻格点之间的隧穿被抑制,并且在BECs的自由膨胀过程中原子间相互作用效应可以忽略,这一点已得到实验证实[14].而同一个格点中的BECs是完全相干的,可以用一个序参量Ψk=[N/(2kM+1)]1/2ϕkexp(iθk)描述,其中ϕk为第k个格点中的单粒子波函数,θk为相干输运前第k个BEC的初始随机相位,i为虚数单位,N为总凝聚原子数,2kM+1为总格点数,系数N/(2kM+1)表示每个BEC的平均粒子数.

假定初始时刻原子处于超精细态|F=1,mF=−1〉k(记为自旋态|0〉k), 应 用 一个任意的α微波脉冲,将原子制备到|F=1,mF=−1〉k和|F=1,mF=−2〉k(记 为自旋态|1〉k)的相干叠加态,自旋态|0〉和|1〉组成原子的逻辑基矢,其变换规则为[25−27]

经历自旋相关输运后,原子的自旋态变为cos(α/2)|0〉k+iexp(iβ)sin(α/2)|1〉k+r[14,25−27],其中r表示输运后自旋态|0〉k和自旋态|1〉k+r波包之间的距离,两个波包之间的相对相位β主要由输运过程中积累的动能和势能相位决定,与凝聚体的粒子数无关.原子的波函数可以用单个原子的内部自由度(自旋)与外部自由度(空间波包)形成的量子纠缠态表示为[25−27]

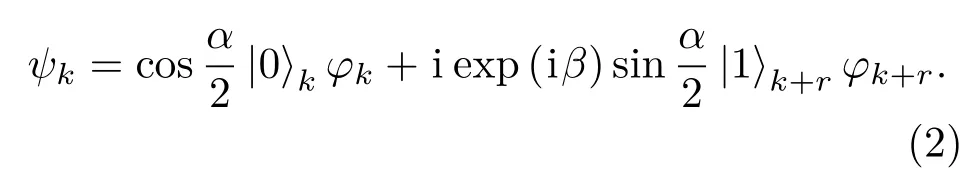
假定空间波包为高斯分布

式中d=λ/2表示光晶格的周期,λ为激光波长,A=1/(σ1/2π1/4)为归一化系数,σ为每个晶格中凝聚体的宽度.应用一个π/2微波脉冲,其变换规则遵循(1)式,可得

其中

考虑到玻色子的全同性原理,(4)式中自旋态|0〉和|1〉的下标已移除.

凝聚体被相干输运后,撤除自旋相关光晶格,让其自由膨胀.与此同时,在原来的自旋相关光晶格中心位置竖立一个无限高的势垒,形成两个左右对称的半无限深势阱,以考察自旋相关BECs在半无限深势阱中的量子反射与干涉动力学.这个无限高的势垒可以利用强聚焦蓝失谐排斥激光束在实验中近似实现.另外,凝聚体的自由膨胀也是冷原子实验中常用的一种探测方案,例如采用自由膨胀能够揭示旋转BECs中的隐涡旋[29,30].因此,本研究在当前实验技术条件下是可行的,理论预言结果能够得以检验.当自旋相关光晶格被关闭后,波函数的空间成分Ψj,k(x,t)(j=0,1)在半无限深势阱中的演化可以用传播子方法求出[31]:

式中Ψj,k(y,t=0)(j=0,1)是初始时刻的空间成分,由(5)式和(6)式给出,Kh(x,y,t)是半无限深势阱的传播子[32],

式中

和

分别为自由空间传播子,m为原子质量,ħ为约化普朗克常数.将(5)式和(6)式代入(7)式进行积分,经过复杂的计算可求得如下解析解:

式中参数γ=ħ/(mσ2)表示光晶格单个阱中的囚禁频率.

考虑原子气体的整体密度分布,t时刻原子气体的波函数为

式中ϕk(x,t)=|0〉Ψ0,k(x,t)+|1〉Ψ1,k(x,t). 因为逻辑基矢|0〉和|1〉是正交的,处于不同自旋态的波包之间不会发生干涉.根据Wen等[25−27]提出的理论模型,由于单个粒子的量子纠缠,每个原子只与它自己发生干涉,这种干涉与各个凝聚体的相位无关.原子气体整体的密度分布表达式为

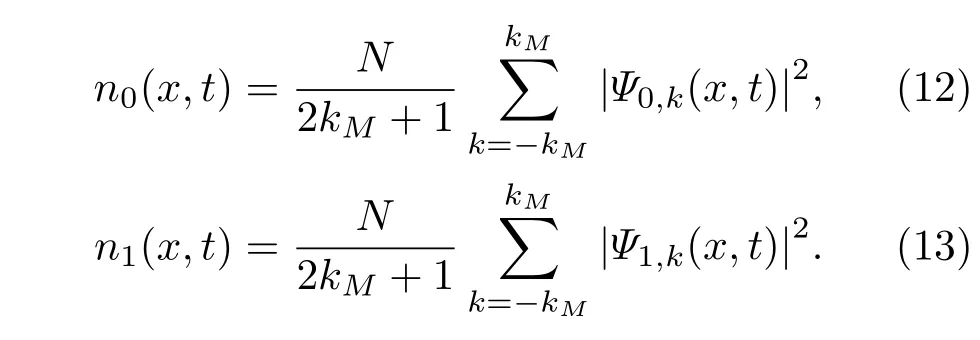
我们根据(12)式和(13)式并采用数值计算分别绘出处于自旋态|0〉和|1〉的原子波包的密度分布及其演化.计算中相关的参数取值与实验[14]中给出的参数值一致,α=π/2,N=3×105,λ=785 nm,d=λ/2,kM∼50[14,25,33].为简单起见,先忽略相对相位,令β=0.后面会考虑相对相位β对干涉条纹的影响,并与忽略β情形进行比较.σ的大小主要由光学约束决定[33],可以采用变分法计算求解,我们的计算结果为σ/d=0.173.

3 结果与讨论

如无特殊说明,由数值计算结果绘出的图形的横坐标皆以晶格周期d为单位,纵坐标皆以H=NA2/(2kM+1)为单位. 当飞行时间t=14 ms,输运距离分别为r=d,2d,3d,4d,5d,6d时,处于自旋态|0〉的密度分布分别由图1(a)—图1(f)给出,处于自旋态|1〉的密度分布分别由图2(a)—图2(f)给出.

图1 半无限深势阱中处于自旋态|0〉的密度分布Fig.1.Density distributions in state|0〉in the semi-in finite potential wells.

图2 半无限深势阱中处于自旋态|1〉的密度分布Fig.2.Density distributions in state|1〉in the semi-in finite potential wells.

从图1和图2可以看出,无论是处于自旋态|0〉还是自旋态|1〉,随着输运距离r的增大,干涉条纹之间的距离都明显减小,干涉条纹的可见度都显著降低.说明随着输运距离的增大,自旋相关BECs的干涉性逐渐减弱.对比处于自旋态|0〉的密度分布,图2(a)—图2(f)中的干涉峰正好对应图1(a)—图1(f)中密度的局部极小值,反之亦然,这个特征可以根据系统的能量守恒和粒子数守恒得到很好的解释.在整个动力学演化过程中,我们没有考虑粒子间的多体相互作用,从而避免了量子反射与干涉过程中可能由多体相互作用导致的集体激发、系统的不稳定性甚至塌缩.

此外,我们发现在干涉条纹的某些对称的峰或谷附近存在剧烈的密度振荡,显然这些振荡条纹是由半无限深势阱壁造成的.严格来讲,这些剧烈的密度振荡所隐含的物理机理是相当复杂的,我们只给出一个简化的物理图像.当关闭自旋相关光晶格后,每个格点中的自旋相关物质波首先发生自由扩散,逐渐接近半无限深阱壁,在此过程中与来自不同格点的相同自旋态的物质波相遇并发生量子干涉,形成干涉条纹的主体.与此同时,不同格点中的自旋相关物质波先后在阱壁上发生反射,反射波与相应的入射波相干叠加发生二重干涉,导致密度的重新分布并形成调制的干涉条纹,这种二重干涉本质上是BECs的自干涉[34].从传播子的表达式((8)式)来看,二重干涉可以看作阱壁作为镜面对自旋相关物质波成像,是自旋相关凝聚体与镜像凝聚体的干涉,一定程度上类似波动光学中的杨氏双缝干涉,并且在阱壁处形成驻波节点.因此,二重干涉形成的局部密度振荡的位置及间距主要与格点到阱壁的距离、晶格宽度、晶格高度、演化时间t四个因素有关,前三个因素本质上是由激光的波长和强度所决定的,以上分析在我们的数值模拟和计算中均已被证实.另外,由于自由膨胀之前自旋相关光晶格的存在,二重干涉导致衍射条纹的出现,即干涉条纹中局部的剧烈密度振荡,这里的衍射现象是来自不同格点的相干波源的干涉结果.

图3 半无限深势阱中(a)处于自旋态|0〉和(b)处于自旋态|1〉的密度分布的局部放大(飞行时间t=14 ms,输运距离r=d)Fig.3.Local enlargement of the density distributions(a)in state|0〉and(b)in state|1〉in the semi-in finite potential wells.The time of flight period t is 14 ms,and the transport distance r is d.

由于横坐标单位的限制,图1和图2中振荡条纹的具体起伏不太清晰,为此我们将干涉条纹的振荡进行局部放大,以比较不同自旋态的干涉条纹的区别,如图3所示.在图3中,我们分别给出了t=14 ms,r=d情形自旋态|0〉和自旋态|1〉干涉条纹的局部放大,考虑到干涉条纹关于中心左右两边对称,因此只绘出左边部分的局部放大.从图3可以看出,在原点附近两种自旋态密度分布中的小振荡都是关于原点对称的,自旋态|1〉的振荡比自旋态|0〉的振荡剧烈,原因是干涉条纹中这两种自旋态的局部极值是相反的(图1和图2),这一点与系统的能量守恒和粒子数守恒是自洽的.对于相同的输运距离,自旋态|0〉和自旋态|1〉的干涉条纹中出现局部密度振荡的位置是重合的.根据前述讨论,这些局部密度振荡造成的干涉调制效应,是由于自由膨胀的自旋相关物质波碰到无限深势阱壁发生量子反射形成的反射波与入射波发生二重干涉引起的.在此过程中,自旋态|0〉和自旋态|1〉的物质波的量子反射与二重干涉是独立的也是同步的.

前文计算中已令β=0,即没有考虑相对相位β是否对干涉条纹产生影响.图4所示为β=−π/12(图4(a)和图4(b)),β=−π/2(图4(c)和图4(d))和β= π/2(图4(e)和图4(f))时系统演化后处于自旋态|1〉的密度分布,相关参数为t=15 ms,r=2d.由图4可以看出,对于半无限深势阱中自旋相关BECs的动力学演化,改变相对相位β的取值,其密度分布及振幅会有所改变,但干涉条纹关于原点左右两边的对称性保持不变,干涉条纹中局部密度振荡所在位置基本不变.根据实验中观察到的干涉图样[14],能够推断出实验中相对相位β的绝对值应该比较小,接近于零.

图4 相对相位β对处于自旋态|1〉的密度分布的影响(飞行时间t=15 ms,输运距离r=2d) (a)β=−π/12;(b)图(a)的局部放大;(c)β=−π/2;(d)图(c)的局部放大;(e)β=π/2;(f)图(e)的局部放大Fig.4.The effect of the relative phase β on the density distributions in state|1〉(the time of flight period t is 15 ms,and the transport distance r is 2d):(a)β= −π/12;(b)local enlargement of(a);(c)β= −π/2;(d)local enlargement of(c);(e)β=π/2;(f)local enlargement of(e).

4 结 论

本文利用传播子方法和飞行时间吸收成像方案,研究了自旋相关BECs在半无限深势阱中的量子反射和干涉演化动力学.在Bloch小组实验的基础上建立了理论模型,推导得到半无限深势阱中自旋相关的凝聚体波函数的严格解析解.对于具体的参数,通过数值计算分别绘制了处于自旋态|0〉和|1〉的密度分布图,在飞行时间一定的情况下,考察了自旋态、输运距离和相对相位对干涉条纹的影响.研究表明,当自旋相关光晶格撤除后,初始处于同一格点的物质波经历π/2脉冲—自旋相关输运—π/2脉冲操作后,非局域于不同格点中相同自旋态的物质波在自由膨胀过程中发生量子干涉,形成了对比度明显的干涉条纹.与此同时,半无限深势阱的存在直接导致自旋相关BECs的量子反射和二重干涉,干涉条纹呈现显著的调制效应,在两边对称的某些干涉峰或谷附近密度分布表现出剧烈的振荡.这些局部密度振荡的位置与间距主要是由演化时间、激光波长和强度所决定的.随着输运距离的增大,干涉条纹间距减小,干涉条纹的可见度显著降低,自旋相关BECs的相干性逐渐减弱,而由量子反射与二重干涉所造成的干涉条纹的调制效应变得更为明显.该研究有利于促进人们对自旋相关BECs物理特性的认识,在当前的冷原子实验技术条件下容易实现,同时也为深入检验自旋相关BECs的理论模型和干涉机理提供了一个新的可行方案.

[1]Andrews M R,Townsend C G,Miesner H J,Durfee D S,Kurn D M,Ketterle W 1997Science275 637

[2]Pasquini T A,Shin Y,Sanner C,Saba M,Schirotzek A,Pritchard D E,Ketterle W 2004Phys.Rev.Lett.93 223201

[3]Pasquini T A,Saba M,Jo G,Shin Y,Ketterle W,Pritchard D E,Savas T A,Mulders N 2006Phys.Rev.Lett.97 093201

[4]Greiner M,Mandel O,Esslinger T,Hänsch T W,Bloch I 2002Nature415 39

[5]Hofferberth S,Lesanovsky I,Schumm T,Imambekov A,Gritsev V,Demler E,Schmiedmayer J 2008Nat.Phys.4 489

[6]Fang B,Johnson A,Roscilde T,Bouchoule I 2016Phys.Rev.Lett.116 050402

[7]Chang R,Bouton Q,Cayla H,Qu C,Aspect A,Westbrook C I,Clement D 2016Phys.Rev.Lett.117 235303

[8]Castellanos E,Rivas J I 2015Phys.Rev.D91 084019

[9]Wen L H,Wang J S,Feng J,Hu H Q 2008J.Phys.B41 135301

[10]Scott R G,Martin A M,Fromhold T M,Sheard F W 2005Phys.Rev.Lett.95 073201

[11]Marchant A L,Billam T P,Yu M M H,Rakonjac A,Helm J L,Polo J,Weiss C,Gardiner S A,Cornish S L 2016Phys.Rev.A93 021604

[12]Berrada T,van Frank S,Bucker R,Schumm T,SchaffJ F,Schmiedmayer J,Julia-Diaz B,Polls A 2016Phys.Rev.A93 063620

[13]Fouda M F,Fang R,Ketterson J B,Shahriar M S 2016Phys.Rev.A94 063644

[14]Mandel O,Greiner M,Widera A,Rom T,Hänsch T W,Bloch I 2003Phys.Rev.Lett.91 010407

[15]Castin Y,Dalibard J 1997Phys.Rev.A55 4330

[16]Yang X X,Wu Y 1999Phys.Lett.A253 219

[17]Liu W M,Wu B,Niu Q 2000Phys.Rev.Lett.84 2294

[18]Xiong H,Liu S,Huang G,Xu Z 2002J.Phys.B35 4863

[19]Liu S,Xiong H,Xu Z,Huang G 2003J.Phys.B36 2083

[20]Xiong H,Liu S,Zhan M 2006New J.Phys.8 245

[21]Bach R,Rzazewski K 2004Phys.Rev.Lett.92 200401

[22]Liu S,Xiong H 2007New J.Phys.9 412

[23]Hadzibabic Z,Stock S,Battelier B,Bretin V,Dalibard J 2004Phys.Rev.Lett.93 180403

[24]Ashhab S 2005Phys.Rev.A71 063602

[25]Wen L H,Liu M,Xiong H W,Zhan M S 2005Eur.Phys.J.D36 89

[26]Wen L H,Liu M,Kong L B,Chen A X,Zhan M S 2005Chin.Phys.14 690

[27]Wen L H,Liu M,Kong L B,Zhan M S 2005Chin.Phys.Lett.22 812

[28]Yue X,Liu S,Wu B,Xiong H 2017Chin.Phys.B26 050501

[29]Wen L H,Xiong H W,Wu B 2010Phys.Rev.A82 053627

[30]Wen L H,Li J H 2014Phys.Rev.A90 053621

[31]Feynman R P,Hibbs A R 1965Quantum Mechanics and Path Integrals(New York:McGraw-Hill Inc.)pp26–74

[32]Akhundova E A,Dodonov V V,Man’ko V I 1985J.Phys.A18 467

[33]Pedri P,Pitaevskii L,Stringari S,Fort C,Burger S,Cataliotti F S,Maddaloni P,Minardi F,Inguscio M 2001Phys.Rev.Lett.87 220401

[34]Robinett W 2006Phys.Scr.73 681

Quantum re flection and interference of spin-dependent Bose-Einstein condensates in semi-in finite potential wells∗

Zhao Wen-Jing Wen Ling-Hua†

(Key Laboratory for Microstructural Material Physics of Hebei Province,College of Science,Yanshan University,Qinhuangdao 066004,China)

14 April 2017;revised manuscript

5 July 2017)

The quantum re flection and interference of Bose-Einstein condensates(BECs)encountering a potential barrier or well is one of the most efficient ways of studying the exotic properties of macroscopic matter waves.As a matter of fact,one can reveal the quantum nature,coherence properties,and many-body effects as well as the potential applications of ultracold atomic gases by virtue of the quantum reflection and interference of BECs.Although there have been extensive investigations regarding the quantum reflection and interference of single-component BECs,so far there have been very few studies regarding those of multi-component BECs.In this work,we investigate the quantum reflections and interferences of spin-dependent BECs in semi-in finite potential wells by using the propagation method and the time of- flight imaging scheme which is widely used in cold atom experiments.We obtain the exact analytical solutions of the spin-dependent condensate wave functions in the semi-in finite potential wells.It is shown that once the spin-dependent optical lattice is switched off the spin-dependent matter wave packets delocalized in different lattice sites interfere with each other during the free expansion.Consequently,the interference fringes with high contrast are formed.At the same time,the expanded spin-dependent matter waves encounter the hard wall of the semi-in finite potential well,which leads to a quantum reflection.There is a double interference between the reflected wave and the freely expanded incident wave,which is characterized by the significant modulation effect in the interference patterns.Concretely,there exist intense density oscillations in several symmetric and local regions of the interference fringes.Essentially,the double interference is a self-interference of BECs,and it results from the interference between the spin-dependent BEC and the BEC image,where the hard wall severs as a mirror plane.Therefore it is similar to Young’s double-slit interference in wave optics,and a standing wave node is formed at the trap wall.In particular,the positions and the intervals of the local density oscillations in the interference patterns are determined by evolution time,laser wavelength and laser intensity,which is verified in the numerical simulations and calculations.In addition,the effects of spin state,transport distance,and relative phase on the interference fringes are analyzed and discussed.The present investigation is helpful in understanding the macroscopic quantum properties of the spin-dependent BECs,and provides a new scheme to test the theoretical model and physical mechanism of the condensate interference in a spin-dependent optical lattice.

spin-dependent Bose-Einstein condensates,semi-in finite potential well,quantum reflection,quantum interference

PACS:03.65.–w,03.75.Kk,03.75.Mn,05.30.JpDOI:10.7498/aps.66.230301

*Project supported by the National Natural Science Foundation of China(Grant No.11475144),the Natural Science Foundation of Hebei Province of China(Grant No.A2015203037),and the Research Foundation for Advanced Talents of Yanshan University,China(Grant No.B846).

†Corresponding author.E-mail:linghuawen@ysu.edu.cn

(2017年4月14日收到;2017年7月5日收到修改稿)

玻色-爱因斯坦凝聚体与势垒或势阱的量子反射及干涉是考察宏观物质波奇特物性的最有效途径之一.利用传播子方法和基于冷原子实验广泛采用的飞行时间吸收成像方案,研究自旋相关玻色-爱因斯坦凝聚体在半无限深势阱中的反射和干涉演化动力学,得到了自旋相关的凝聚体波函数的严格解析解.结果表明,当自旋相关光晶格关闭后,非局域于不同格点中相同自旋态的物质波在自由膨胀过程中发生量子干涉,形成了对比度明显的干涉条纹.与此同时,扩张的自旋相关物质波包与半无限深势阱壁相遇发生量子反射,反射波与入射波产生二重干涉,在密度分布两边对称的局部位置出现剧烈的振荡,干涉条纹表现出显著的调制效应.分析讨论了自旋态、相干输运距离和相对相位等因素对干涉条纹的影响.该研究有助于促进对自旋相关凝聚体宏观量子特性的认识,为深入检验自旋相关光晶格中凝聚体干涉的理论模型和物理机理提供依据和新方案.

10.7498/aps.66.230301

∗国家自然科学基金(批准号:11475144)、河北省自然科学基金(批准号:A2015203037)和燕山大学人才引进科研启动基金(批准号:B846)资助的课题.

†通信作者.E-mail:linghuawen@ysu.edu.cn