非最大纠缠GHZ 态的受控量子隐形传态

王 娜， 章志华*， 张嘉敏， 舒 兰

（1.江苏大学 理学院，江苏 镇江212013； 2.电子科技大学 数学科学学院，四川 成都611731）

量子隐形传态方案最早在1993 年由Bennett等［1］提出.此方案中有一待传送的单量子未知态，发送者和接收者共享一个EPR 对作为量子纠缠信道.发送者对自己手中的粒子进行一次Bell基测量并通过经典信道将测量结果告诉接收者.接收者作相应幺正变换重构待传送态，从而完成隐形传态.此后，许多学者开始了对隐形传态的研究：Cao等［2］利用W 态作为信道实现二粒子隐形传态，Yang等［3］提出三粒子纠缠态隐形传态方案；特别地，Nielsen［4］提出了以非最大纠缠态作为量子信道实现隐形传态，随后关于这方面的方案也相继被提出.

可控量子隐形传态是在1998 年由Karlesson等［5］首次提出，其中利用的量子信道为GHZ态.在可控量子隐形传态中除了发送者和接收者还多了一个控制者，发送者想将信息传送给接收者需要向控制者提出申请，待控制者同意后才能进行隐形传态.近年来，一些可控隐形传态方案被相继提出.刘俊昌等［6］基于纠缠交换和团簇态实现任意二粒子态的可控隐形传态，胡钰安等［7］提出基于四粒子GHZ态的可控量子双向隐形传态方案.

在量子隐形传态中，三粒子纠缠态的隐形传态一直是人们研究的热点问题.Dur 等［8］在研究三粒子纠缠态时发现，可将任意三粒子纠缠态转换为纠缠GHZ态和纠缠W态，因此纠缠GHZ态的传送成为值得研究的问题.如刘秀等［9］提出利用三粒子部分纠缠GHZ 态概率隐形传送三粒子GHZ 态的方案，李艳玲等［10］利用单个三粒子最大GHZ 态或2个EPR态隐形传送任意三粒子GHZ态，臧鹏等［11］利用2 个EPR对实现三粒子GHZ态的控制隐形传态方案.W态在结构上相较GHZ态更稳定，不易被破坏［12］，W态作为信道可以提高隐形传态的安全性.杨洪钦等［13］提出利用三粒子W态隐形传送三粒子GHZ态的方案，查新未等［14］提出利用一个三粒子W态隐形传送N粒子GHZ态的方案.本文考虑到隐形传态的可控性和安全性问题，提出利用一个非最大纠缠EPR 对和一个四粒子GHZ 态、一个非最大纠缠的EPR对和W态分别作为信道隐形传送任意三粒子GHZ态的方案.

1 方案1：利用一个非最大纠缠EPR对和一个非最大纠缠的四粒子GHZ态的隐形传态

假定Alice和Bob传送的未知态为GHZ态，表示为

Alice和Bob共享的量子信道为一个非最大纠缠的EPR对和一个非最大纠缠的四粒子GHZ态的复合

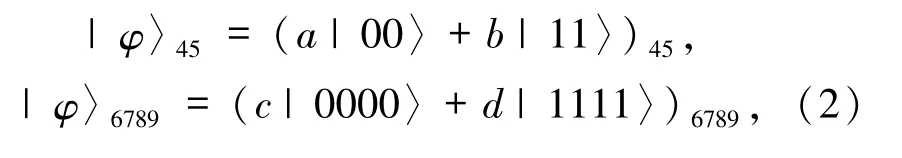
其中，参数满足｜a ｜2+ ｜b ｜2=1 和｜c ｜2+ ｜d ｜2=1.Alice拥有粒子1、2、3、4，Bob拥有粒子6、8、9，粒子5、7 属于控制者Charlie.量子信道为

Alice要将信息传递给Bob 需向控制者Charlie提出申请，若Charlie 同意Alice 的申请，则对粒子5、7 进行Bell基联合测量.Bell基形式为：

Bell基联合测量后，粒子4、6 建立联系.Charlie将测量结果通过经典信道告诉Bob.如果Charlie的测量结果为｜Φ+〉57，则量子信道坍缩态为

此时待传送态和量子信道的总量子态（除归一化因子）为

接着，Alice 对自己手中的粒子1、4 进行Bell基测量，测量后系统量子态为如下几种情况：

假定Alice的测量结果为｜Ψ+〉14，则量子态坍缩态为

接下来，Alice将粒子2、3 在基｛｜+〉、｜-〉｝下分别进行2 次单粒子von -Neumann 测量，测量后粒子6、8、9 坍缩态为：

Alice将测量结果通过经典信道告诉Bob，Bob根据Charlie和Alice的测量结果对粒子6、8、9 作相应的幺正变换.粒子6、8、9 的状态（除归一化因子）和相应的幺正变换由表1 给出，其中UT 为Unitary transformation缩写，下同.

表1 对应粒子6、8、9 的态Bob所实施的幺正变换Tab.1 UT by Bob corresponding to different states of particle 6，8 and 9

例如，如果Charlie 的测量结果为｜Φ+〉57，Alice的测量结果为｜Ψ+〉14、｜+〉2、｜+〉3，则粒子6、8、9 的坍缩态（除归一化因子）为

由上式可以看出，Bob 通过变换之后不能得到原来的态，因为非最大纠缠信道已使得被传送的量子态发生变化，含有了信道参数a、b、c、d，因此引进初态为｜0〉的辅助粒子A，并且以基｛｜0000〉689A、｜1110〉689A、｜0001〉689A、｜1111〉689A｝进行U变换

其中，Ai（i=1，2）为2 ×2 的对角矩阵，表示为

其中，｜bi｜≤1，i =1，2 且其值依赖于粒子6、8、9、A的态.对于粒子6、8、9、A 所处的态（除归一化因子），矩阵元b1、b2的取值由表2 给出.

表2 粒子6、8、9、A所处的态对应矩阵元b1、b2的值Tab.2 The states of particle 6，8，9 and A corresponding to the value of the matrix element b1 and b2

对于态

最后，Bob 对粒子A 进行测量，若测量结果为｜1〉A，则隐形传态失败；如果测量结果为｜0〉A，则隐形传态成功且成功的概率为因此，方案1 的总成功概率为

2 方案2：利用非最大纠缠的EPR 对和非最大纠缠W态的隐形传态

Alice 发送给Bob 的未知态为（1）式.Alice 和Bob共享的量子信道为一个非最大纠缠的EPR 对和一个非最大纠缠的W态，表示为

其中，参数满足｜a｜2+ ｜b｜2+ ｜c｜2+ ｜d｜2=1， ｜e｜2+ ｜f｜2=1.

设Alice拥有粒子1、2、3、4，Bob拥有粒子6、8，粒子5、7 属于控制者Charlie.

为了更好地完成隐形传态，将W 态以4 粒子为控制位，5、6 粒子为靶位，分别做2 次CNOT 操作，W态变换为

此时的量子信道为

Alice 想要将信息传递给Bob 就必须要向控制者Charlie提出申请，若Charlie同意Alice的申请则对粒子5、7 进行Bell 基联合测量，Bell 基由（4）式给出.Charlie通过经典信道将测量结果告诉Bob.

假定Charlie 的测量结果为｜Φ+〉57，量子信道坍缩态（除归一化因子）为

待传送态和量子信道的总量子态（除归一化因子）为

首先，Alice 对粒子1 和4 进行Bell基测量，测量后粒子2、3、6、8 坍缩态（除归一化因子）为：

接着，Alice对粒子2、3在基｛｜+〉，｜-〉｝下分别进行单粒子von -Neumann 测量，并将测量结果通过经典信道告诉Bob.如果Bob 收到的结果为｜Φ+〉14、｜+〉2、｜+〉3，那么粒子6、8坍缩态（除归一化因子）为

Bob引入2 个初态都为｜0〉的粒子A、B 并对粒子6进行单粒子测量，测量结果（除归一化因子）为：

由上式可以看出如果测量结果为｜0〉6，隐形传态直接失败；如果测量结果为｜1〉6，隐形传态可以继续.Bob根据Alice 和Charlie 的测量结果对态｜ψ〉8AB（除归一化因子）进行幺正变换并由表3 给出.

表3 对应粒子8、A、B的态Bob所实施的幺正变换Tab.3 UT of Bob corresponding to different states of 8，A and B

假定Charlie的测量结果为｜Φ+〉57，Alice的测量结果为｜Φ+〉14、｜+〉2、｜+〉3，Bob 的测量结果为｜1〉6，由表3可知，进行恒等变换后（除归一化因子）为

接着，Bob以粒子8 为控制位，粒子A、B 为靶位分别作2 次CNOT操作，得到

然后，Bob引入初态为｜0〉的粒子C并且以基｛｜0000〉，｜1110〉，｜0001〉，｜1111〉｝8ABC进行U 变换，矩阵U由（11）式给出.其中，bi（i =1，2）的值依赖于粒子8、A、B、C的态.对于粒子8、A、B、C所处的态（除归一化因子），矩阵元b1、b2的取值由表4 给出.

表4 粒子8，A、B、C的状态及其对应的矩阵元b1、b2的值Tab.4 The state of particle 8，A，B and C corresponding to the value of the matrix element b1 and b2

对于态

最后，Bob对粒子C进行测量，若测量结果为｜1〉C，则隐形传态失败；如果测量结果为｜0〉C，则隐形传态成功且成功的概率为因此，方案2 的总成功概率为

3 结论

本文提出2种方案用于非最大纠缠GHZ态的受控量子隐形传态.这2种方案相对于之前的GHZ态隐形传态在可控性和安全性上都有一定的优点，同时也在保证成功率的情况下减少了一定的测量过程.本文的方案相比于文献［10，13-14］有以下优点：

1）本文的信道中加有控制者，这一点大大提高了隐形传态的安全性.

2）本文采用非最大纠缠的量子态作为信道，使得结论更具有一般性.

3）由文献［12］知道W 态比较稳定，不易破坏，用W态作为信道可以提高安全性.方案2 以一个非最大纠缠的EPR对和一个非最大纠缠的W态为信道，较文献［10 -11］中以2 个EPR 对作为纠缠信道隐形传态过程更加安全.

本文与其他可控量子隐形传态的不同在于，与文献［7］中2 个四粒子GHZ态为信道相比，本文采用的量子信道为Bell 态和三粒子GHZ 态更易制备，从而节省了信道资源.本文相较文献［11］在成功率相同的情况下，测量次数和幺正变换次数都有减少，这使得隐形传态过程更简便.相比文献［12］，本文中发送者需征求控制者同意后，通过纠缠交换使发送者和接收者之间建立纠缠信道才可进行隐形传态，因此安全性更进一步提高.