基于MonteCarlo模拟的环形链在均质表面的吸附性质研究

孙立望 李洪

摘  要： 基于Monte Carlo模拟方法以及模拟退火算法研究了环形链在均质表面的吸附性质。采用规则生成法生成环形链，模拟退火算法模拟了48个从较高到极低的温度集合，并在每个温度下运行足够的蒙特卡洛步以达到平衡。发现环形链在均质表面吸附的形状因子在相同的条件下小于线性链的形状因子。采用插值法计算了环形链在均质表面吸附的临界温度以及交叉指数，发现环形链的临界吸附温度略大于线性链，交叉指数略小于线性链。这为更深入地研究环形链提供了理论基础。

关键词： Monte Carlo模拟; 环形链; 模拟退火; 临界温度

中图分类号：TP391          文献标志码：A     文章编号：1006-8228（2019）10-24-04

Abstract： The adsorption of the ring polymer on the homogeneous surface is studied based on Monte Carlo simulation method and annealing algorithm. A rule generation method is used to generate the ring polymer， and a simulated annealing algorithm is used to simulate 48 temperature sets from higher to very low， and enough Monte Carlo steps are run at each temperature to achieve equilibrium state. It is found that the shape factor of the ring polymer adsorbed on the homogeneous surface is smaller than that of linear polymer under the same conditions. The critical temperature and cross-index of the adsorption of the ring polymer on the homogeneous surface are calculated by interpolation method， and find that the critical adsorption temperature of the circular chain is slightly larger than that of the linear chain， and the cross-index is slightly smaller than that of the linear chain. This provides a theoretical basis for the more in-depth study of the ring polymer.

Key words： Monte Carlo simulation; ring polymer; annealing algorithm; critical temperature

0 引言

有关线性链在吸附表面的、在溶液中的吸附和扩散性质已经有许多研究人员进行了研究[1-4]。在模拟退火的过程中，线性链的形状因子从0.44变化到0.63，而环形链与线性链相比存在一个结构上的差异（没有链端），因此对于环形链形状因子的变化规律的研究亦是必要的。同时从之前的研究我们可以知道环形链由于其特殊的拓扑结构会排斥表面，因此对其吸附性质的研究也非常重要[5-9]。高分子链的临界吸附点作为高分子聚合物吸附作用的一个重要性质，可以用来描述聚合物吸附的难易度。从之前的研究我们可以知道线性链在均质表面的临界吸附点[Tc]=1.65，但是对于环形链来说，这个临界吸附点是否会发生改变仍然是个未知的问题。

1 模型与方法

我们采用计算机模拟中比较经典的简立方格子模型来模拟环形链在均质表面的运动。我们将链长N=200的环形链生成后放入大小为[144×144×50]的简立方格空间中，其中我们在格子空间的XOY平面上设置周期性边界条件，在[Z=1]处设置一个均质的吸附表面，在[Z=50]处设置一个不可穿透的挡板，此挡板的作用是防止环形链远离吸附表面使得实验结果产生较大的误差。对于环形链的生成，我们采用规则生成的方法，其一是因为自回避生成算法并不适合环形链，其二是由前面的重要性抽样可以知道，为了排除初始構象的影响，我们的数据计算是从中间的某个时刻开始的。高分子单体之间的键长取值限制为[1、2]和[3]，其他的取值均不合法。

2.2 环形链的标度指数与形状因子

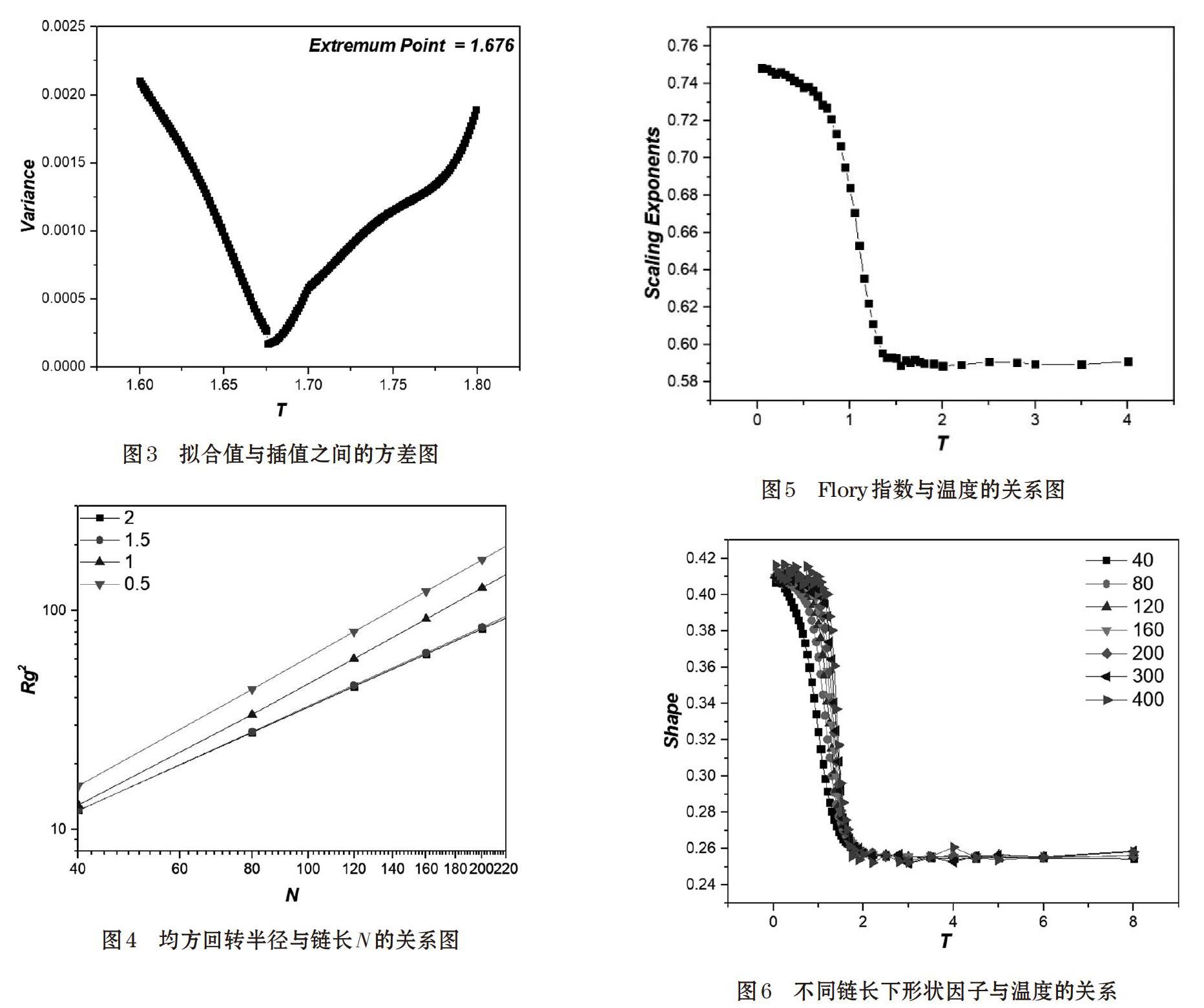
线性高分子链的回转半径[Rg]与链长[N]之间标度关系可以表示为[Rg∝Nv]，这里的[v]指的是Flory 指数，其作用在于描述特定条件下高分子链的尺寸随着链长增长时的变化率。因此我们研究环形链的回转半径[Rg]与链长[N]之间是否有类似的规律，这里我们选取了四个温度[T=0.5， 1.0， 1.5， 2.0]，标度关系如图4所示。

对图4的数据采用双对数处理，发现成正比关系，因此环形链也满足表达式[Rg∝Nv]，而且我们可以粗略看出温度越低斜率越大，所对应的Flory指数也越大。由于Flory指数的大小与环境有着至关重要的联系，所以我们改变温度来研究环形链的Flory指数随着温度的变化关系，如图5所示。

从图5可以看出，环形链在高温时的标度指数等于0.58，这和线性链在自由空间的运动相一致。在极低温的情况下，标度指数等于0.75，和线性链在二维空间中的运动相一致。这是因为高温下均质表面对环形链几乎没有吸附作用，因此等同于在自由空间运动，在极低温的情况下环形链全部吸附在表面，因此环形链只能在均质表面做二维运动，这也说明了无论是二维自由空间还是三维自由空间，环形链与线性链的回转半径与链长的标度关系是一致的。同时我们也可以看出，在部分受限的情况下（除去高温与极低温的其他温度）环形高分子链在均质表面的标度指数[v∈0.588，   0.75]。

通過研究我们知道，均质表面的线性链在模拟退火的过程中，其形状因子的变化范围为[shape∈0.45， 0.63]，由于形状因子[shape=0]时高分子链处于球状，形状因子[shape=1]时，高分子链为杆状，因此我们可以将形状因子[shape]从0到1的过程看作将球体先压平后拉长的过程。我们选取了不同链长的样本对形状因子进行研究，如图6所示。

从图6我们可以看出，形状因子的变化范围是[shape∈0.25， 0.41]，明显小于线性链的形状因子变化，这是因为环形链没有链端，它并不像线性链那样容易被拉伸，因此环形链的形状因子明显小于线性链。而且可以看出随着温度的降低，链长越长的环形链其形状稳固所需的温度越高，即所需要的作用力就越小，这也就说明了链长越长，环形链受结构约束所造成的影响就越低，因此就越容易到达稳定的形状。

3 结束语

本文采用基于重要性抽样采用规则生成法生成环形链，采用键长涨落的方法使环形链进行运动。分析了环形链在均质表面运动的各项性质。采用插值法计算了环形链的临界吸附温度以及交叉指数，环形链的临界吸附温度略大于线性链的临界吸附温度，其交叉指数略小于线性链。环形链的标度指数在不同的温度下变化范围为[v∈0.588，   0.75]。环形链的形状因子变化范围为[shape∈0.25， 0.41]，小于线性链的形状因子。这使得我们对于环形聚合物在均质表面的吸附有了更加深刻的理解，对高分子材料的合成也有一定的指导意义。接下来我们将研究环形聚合物在条纹表面的吸附性质，观察并计算其在均质表面的性质差异。

参考文献（References）：

[1] Li，Hong，et al. "Critical adsorption of a flexible polymer on a stripe-patterned surface." Soft matter 11.16 （2015）：3222-3231

[2] Li H，Qian C J，Luo M B.Simulation of a flexible polymer tethered to a flat adsorbing surface[J].Journal of Applied Polymer Science，2012.124（1）： 282-287

[3] Li H，Qian C J，Sun L Z，et al.Conformational properties of a polymer tethered to an interacting flat surface[J]. Polymer journal，2010.42（5）：383.

[4] Li H，Qian C J，Wang C，et al. Critical adsorption of a flexible polymer confined between two parallel interacting surfaces[J].Physical Review E，2013.87（1）：012602

[5] Brown S，Szamel G.Computer simulation study of the structure and dynamics of ring polymers[J]. The Journal of chemical physics，1998.109（14）：6184-6192

[6] Suzuki J，Takano A，Matsushita Y.Topological effect in ring polymers investigated with Monte Carlo simulation[J].The Journal of chemical physics，2008.129（3）：034903

[7] Suzuki J，Takano A，Matsushita Y.Chain conformations of ring polymers under theta conditions studied by Monte Carlo simulation[J].The Journal of chemical physics， 2013.139（18）：184904.

[8] Suzuki J，Takano A，Deguchi T，et al.Dimension of ring polymers in bulk studied by Monte-Carlo simulation and self-consistent theory[J].The Journal of chemical physics， 2009.131（14）：144902.

[9] Brown S，Szamel G.Computer simulation study of the structure and dynamics of ring polymers[J].The Journal of chemical physics，1998.109（14）：6184-6192