离散信道信道容量的计算
余秀玲
(西南石油大学,四川 成都 610500)
1 信道容量
最简单的通信系统由信源、信道和信宿组成。对于信道来说,在信道固定的前提下,传输的信息量当然是越多越好,因此信道容量问题是信道研究的重点。信道容量是信道传输信息的最大能力,由信道特性决定。对于特定的信道,信道容量是个定值。根据平均互信息的凸函数性,平均互信息量I(x;y)是输入信源概率分布{p(ai),i=1,2,…,n}的上凸函数,在固定信道的的前提下,平均互信息量有最大值,即信道容量一定存在。但是,在传输信息时,信道能否提供其最大传输能力或者说能否达到信道容量,取决于两点:信源离散无记忆;信源的输入概率分布是使I(x;y)最大的分布。下面给出离散无记忆信道容量的定义:

2 几种特殊离散信道信道容量的计算
离散信道分为多符号离散信道和单符号离散信道,下面针对单符号离散信道进行讨论,给出三种特殊对称信道的信道容量计算方法。
2.1 对称离散信道
对称信道的转移概率矩阵中的每一行都是同一集合{p1,p2,…,pk} 各元素的不同排列,每一列都是同一集合{y1,y2,…,yc}各元素的不同排列。设输入信源概率分布为X:{p(a1),p(a2),…,p(ac)},输出概率分布为Y:{p(b1),p(b2),…,p(bk)},根据信息论的理论及相关结论,可以求得噪声熵:
=H(p1,p2,p3,…,pk)
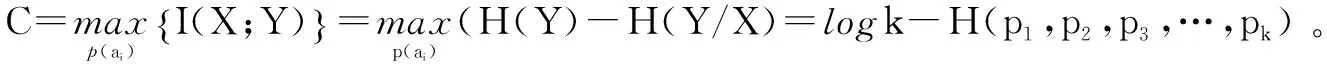
2.2 强对称离散信道
强对称离散信道是特殊的对称信道,强对称信道的概率转移矩阵的每一行和每一列都是同一集合各元素{p1,p2,…,pk}的不同排列,所以行数等于列数,概率转移矩阵一定为方阵,行与列的元素是可排列的。因此当然可以表示为C=logk-H(p1,p2,p3,…,pk),同样当输入为等概率分布时,强对称信道达到其信道容量。
2.3 准对称离散信道

C=-(2×0.375·log0.375+2×0.125·log0.125)+(0.5log0.5+0.25log0.25+0.125log0.125+0.125log0.125)=0.0612(bit/sign)
故该准信道矩阵的信道容量为0.0612 bit/sign.由于该信道为准对称信道,所以不存在等概率输入就有等概率输出的结论,此时达到信道容量满足的条件是调整信源的输入概率分布,使得输出为等概率分布,则达到信道容量。
3 一般离散信道信道容量的计算
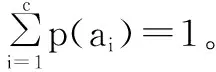
4 结论
信道的信道容量计算是信道问题的研究重点,也是比较复杂的问题。对于特殊离散信道如对称离散信道、强对称离散信道和准对称离散信道,对称离散信道和强对称离散信道的信道容量求解比较简单,两种信道要注意区分不同,相同点是两者达到信道容量的条件都是输入等概率分布。准对称信道容量的求解比较复杂,要将其概率转移矩阵先转变为若干个对称子集,再求解容量,至关重要的一点,准对称信道达到容量的条件是输入的概率分布是使得输出等概率分布的分布。此时,对于准对称,输入等概率不一定使得输出等概率。当然,除了特殊离散信道,就是一般离散信道,那么对于一般离散信道容量的求解,按照四个步骤进行,其中重点是必须求解输入概率分布,检验输入概率矩阵是否都大于零,若满足都大于零,则C即所求;若不满足,则上述C不存在,使用迭代算法重新求解。因此,在求解离散信道信道容量时,首先判断信道的类型,再采取对应的解决方案。
[1] 姜丹.信息论与编码[M].北京:中国科学技术大学出版社,2001.
[2] 周荫清.信息理论基础[M].北京:北京航空航天大学出版社,2002.
[3] 陈运, 周亮, 陈新.信息论与编码[M].北京:电子工业出版社,2005.

