高分子链构象与纳米颗粒尺寸的关系

李 越，郭金权，李朝阳

(杭州师范大学理学院，浙江 杭州 310036)

高分子链构象与纳米颗粒尺寸的关系

李 越，郭金权，李朝阳

(杭州师范大学理学院，浙江 杭州 310036)

高分子链；纳米颗粒；蒙特卡罗；构象

高分子材料(塑料、橡胶、涂料等)广泛地应用于科学技术、国防建设和国民经济等各个领域中，但是单一组分的高分子材料往往难以满足生产生活的需求.如何改善高分子材料的性能，是近几年软物质领域重要的研究课题.研究表明，在高分子材料中添加纳米颗粒，复合粘结成高分子/纳米颗粒复合材料，可以极大地提升材料的性能.例如，在橡胶中加入碳黑颗粒[1-3]，可以增加橡胶的抗压性能，提高橡胶材料的韧性和强度.Mackay等[4]发现，添加纳米颗粒可以减低高分子材料的粘性，而Zhang等[5]却发现纳米颗粒使材料的粘性提高.这些现象说明纳米颗粒对高分子材料性能的影响是非常复杂的，高分子材料的性能与纳米颗粒的尺寸、分布、形状以及高分子链-纳米颗粒之间的作用强度等诸多因素有关.本文通过计算机模拟的方法重点考察了纳米颗粒的尺寸对高分子链构象的影响.

1 模型及模拟算法

模拟计算在一个大小为L×L×L的无格点三维立方系统中进行.为消除界面效应，系统的3个方向均采用周期性边界条件.模拟系统中有一条链长为N的高分子链，为简化计算，高分子链采用粗粒化模型.组成高分子链的球形单体性质相同，直径为σ.模拟系统中心有一个固定不动的球形纳米颗粒，其直径用σn表示.将高分子链单体的直径σ视为长度单位1，纳米颗粒直径σn分别取1，2，…，6，考察这些不同大小的纳米颗粒对链长N= 64的高分子链的构象的影响.模拟系统长度L取30，链长N= 64的高分子链在稀溶液中的平均回转半径RG0≈4.1[6].L远大于2RG0，可以避免高分子链通过周期性边界条件与自身相互作用.

高分子链的任意2个单体间存在Lennard-Jones (LJ)势能：

(1)

(2)

式中2个单体的平衡距离req= 0.8，允许的最大键长rmax= 1.3， 弹性系数kF= 100kBT/2.其中kB是玻尔兹曼常数，T是系统温度.另外，高分子链单体与纳米颗粒之间也考虑LJ势能的作用，形式与式(1)相似，单体与纳米颗粒之间LJ势能的作用强度用εpn表示.

为了得到高分子链构象的统计结果，在蒙特卡罗(MC)模拟中采用了metropolis算法，并且定义高分子链单体的100次随机运动所需的时间为一个时间单位(Monte Carlo Step，MCS).MCS是随意定义的，在实验或分子动力学(MD)模拟中可以转化为实际的时间单位.高分子链的构象大小用均方回转半径表示.为考察纳米颗粒对的影响，本文只计算高分子链与纳米颗粒有接触时的情形.

2 结果与讨论

箭头表示链长N = 64的高分子链在稀溶液中的均方回转半径0 = 16.8.图1 高分子链均方回转半径随高分子链-纳米颗粒相互作用强度εpn的变化关系Fig. 1 Plots of the mean square radius of gyration of polymer versus the polymer-nanoparticle interaction strength εpn

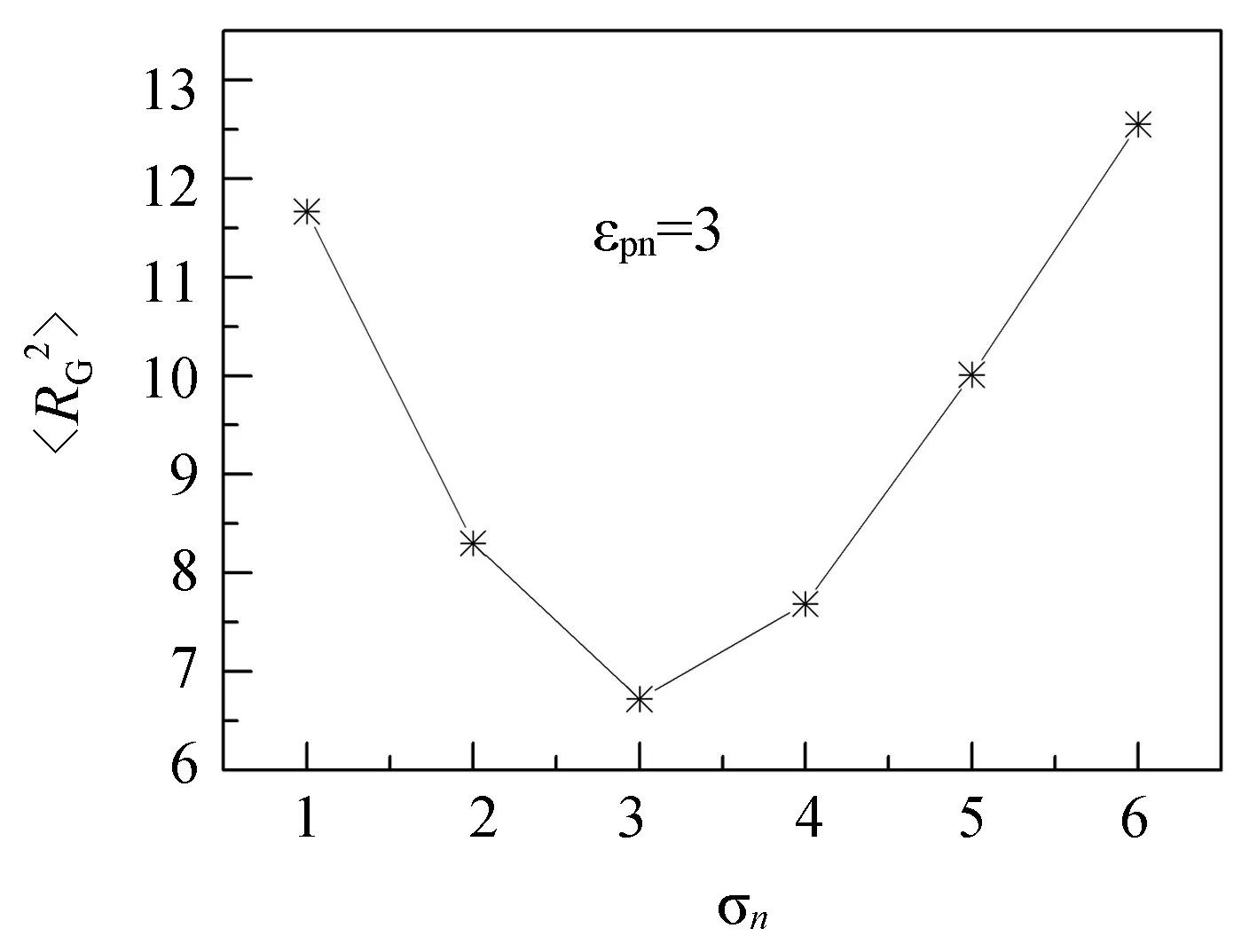
图2 当高分子链-纳米颗粒相互作用强度固定时，高分子链均方回转半径随纳米颗粒直径σn的变化关系Fig. 2 Plots of the mean square radius of gyration of polymer versus the diameter of the nanoparticle σn at εpn = 3

(a):σn =1;(b):σn =3;(c):σn = 6.图3 高分子链-纳米颗粒平均接触数与纳米颗粒直径σn的关系Fig. 3 Plots of the mean number of monomers contacted by nanoparticle versus the diameter of nanoparticle σn

当εpn较大时，纳米颗粒对高分子链产生强烈的吸引作用.如果纳米颗粒的直径σn比较小，其表面积只能容纳少量的几个高分子链单体，没有被吸附的单体仍然像无规线团一样游离于纳米颗粒之外.随着σn的增加，纳米颗粒表面能容纳较多高分子链单体时，高分子链的均方回转半径将变得越来越小.当σn= 3σ时，高分子链的所有单体包围在纳米颗粒周围，达到最小.当单体与纳米颗粒表面靠近、甚至接触的时候，二者间的LJ势将急剧减小.因此，本文定义单体与纳米颗粒的表面距离小于0.5σ时，即认为该单体已经“接触”到纳米颗粒表面了.如果高分子链有单体与纳米颗粒表面接触，则高分子链-纳米颗粒之间的接触能U=ncεpn.当σn> 3σ时，纳米颗粒表面已能吸附容纳所有的单体.为了使得接触能U最低，所有单体会尽可能地平铺在纳米颗粒表面.纳米颗粒越大，其表面越平坦，高分子链将在纳米颗粒表面充分铺展，相应地，将随σn的增加而增加.

为了进一步验证上述分析，笔者计算了高分子链与纳米颗粒之间的单体“接触”数nc.图3所示是εpn= 3时平均接触单体数目随纳米颗粒直径σn的变化关系.在σn= 1时非常小，只有少量的几个单体被吸附在纳米颗粒表面，图3(a)是在模拟过程中随机获取的典型构象.随着σn的增加，不断增加，当σn= 3时，绝大部分单体把纳米颗粒包围起来，形成类似于图3(b)的构象.随着σn的进一步增加，高分子链-纳米颗粒接触数增加得非常缓慢并趋于饱合，整条高分子链延伸以后吸附在纳米颗粒表面，其典型的构象如图3(c)所示.

3 结论

应用蒙特卡罗方法研究了高分子链在不同尺寸的纳米颗粒表面的构象，发现高分子链的均方回转半径依赖于高分子链-纳米颗粒之间的相互作用强度εpn和纳米颗粒的直径σn.当εpn比较小时，高分子链的均方回转半径几乎不受纳米颗粒影响.当εpn比较大时，高分子链的均方回转半径随εpn的增加而减小.当εpn固定时，高分子链的均方回转半径先随σn的增加而减小，在σn=3时达到最小值，随后均方回转半径随σn的增加而增大.

[1] NDORO T V, VOYIATAIS E, GHANBARI A A, et al. Interface of grafted and ungrafted silica nanoparticles with a polystyrene matrix: atomistic molecular dynamics simulations[J]. Macromolecules,2011,44(7):2316-2327.

[2] RANDALL A M, ROBERTSON C G. Linear-nonlinear dichotomy of the rheological response of particle-filled polymers[J]. Journal of Applied Polymer Science,2014,131(19):5829-5836.

[3] KIRCHBERG S, HOLLANDER U, MOHWALD K, et al. Processing and characterization of injection moldable polymerparticle composites applicable in brazing processes[J]. Journal of Applied Polymer Science,2013,129(4):1669-1677.

[4] MACKAY M E, DAO T T, TUTEJA A, et al. Nanoscale effects leading to non-einstein-like decrease in viscosity[J]. Nature Materials,2003,2(11):762-766.

[5] ZHANG Y M, GE S, TANG B, et al. Effect of carbon black and silica fillers in elastomer blends[J]. Macromolecules,2001,34(20):7056-7065.

[6] LI C Y, ZHANG S, HUANG J H, et al. Size and diffusion of polymer in media filled with periodic fillers[J]. e-Polymers,2014,14(1):35-41.

[7] LI C Y, QIAN C J, YANG Q H, et al. Study on the polymer diffusion in a media with periodically distributed nano-sized fillers[J]. Journal of Chemical Physics,2014,140(10):104902.

OntheRelationsBetweentheConfigurationofPolymerChainandtheSizeofNanoparticle

LI Yue， GUO Jinquan， LI Chaoyang

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

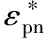
polymer chain； nanoparticle； Monte Carlo； configuration

2017-04-20

浙江省自然科学基金项目(LY15A040009).

李朝阳(1975-)，男，讲师，主要从事高分子模拟计算研究.E-mail:zjlcy@163.com

10.3969/j.issn.1674-232X.2017.06.019

O631.1

A

1674-232X(2017)06-0672-04