三乙胺分子构象与红外光谱的理论研究*
邱梓恒 Ahmed Yousif Ghazal 龙金友† 张嵩‡
1) (中国科学院精密测量科学与技术创新研究院,波谱与原子分子物理国家重点实验室,武汉 430071)
2) (中国科学院大学,物理科学学院,北京 100049)
3) (Engineering Technical College of Mosul,Northern Technical University,Mosul 41002,Iraq)
利用密度泛函理论B3LYP 的方法,在6-311++G(d,p)基组水平上沿二面角φ1(C9N1C2C5)和φ2(C16N1C9C12)构成的二维坐标下扫描了—180°—180°范围内构象异构化势能面,甄别出12 种三乙胺基态异构体.进一步辅以二阶微扰理论MP2 的方法,在相同基组水平下计算与优化6 种能量较低的构象异构体的结构与能量.结果表明具有C3 对称性的G1 与G1′是最稳定构象,并识别出两种具有新的甲基取向的G4 与G4′构象异构体.另外,通过G1—G4 红外光谱与振动模式的比较,分析了它们之间的相似性与差异性.G1—G4 的红外谱线显示在0—1600 cm—1 范围内的强度较弱,而在2800—3300 cm—1 范围内的强度较强,标定出伞状振动与C—H伸缩振动等特征振动模,不同构象所引起的红外谱峰的平均移动量小于20 cm—1.
1 引言
分子构象,是指通过分子内单键旋转而发生异构化后形成的不同的分子空间结构形态,与生物功能息息相关.例如,蛋白质生物大分子的空间构象决定着蛋白质分子的一级结构以及氨基酸的排列顺序,进而决定了蛋白质的生物学功能.分子构象不仅存在于具有低构象自由度的刚性分子,也普遍存在于具有高的构象自由度的柔性分子.柔性分子构象异构体之间的能量相差非常小(约为0—42 kJ·mol—1或0—435 meV)[1,2],这些构象异构体在室温下可以迅速相互转换,并以一定比例形成动态平衡.由于柔性分子具有较高的构象自由度,目前无论从理论上还是实验上对柔性分子的丰富的构象异构体结构的识别以及其构象异构动力学过程的观测依然具有相当大的困难.近些年来,人们逐渐将研究重点放在一些柔性小分子体系上,期望研究结果可以为蛋白质等大分子的构象研究提供相应的信息和有力的指导.Gosselin 等[3]首次提出利用分子里德堡电子结合能的变化来探测柔性分子结构变化的方法,并成功地实现对一些胺类分子的构象结构的甄别与标定[4-7].Dian 等[8]利用激光光谱学方法直接测定出色胺分子构象异构体互相转换的能量阈值.
三乙胺(triethylamine)是叔胺类中相对分子复杂程度较小的柔性分子,拥有3 个C-N 单键和3 个C—C 单键,结构如图1 所示.三乙胺分子内的C—N 与C—C 单键的旋转,导致了3 个乙基链末端的甲基方向的不同,使得三乙胺分子具有丰富的构象异构体.Kumar[9]指出三乙胺基态存在27 种构象异构体,并利用拉曼光谱方法分辨出在液相与固相下的2 种稳定构象异构体TGG′与GGG,而在气相中稳定的构象为TGG′构象异构体.其中,T 代表乙基链末端甲基的Trans 取向,即C5H3,C12H3和C19H3甲基基团与N 原子分别位于三个乙基链中间的碳原子C2,C9 与C16所构成的CCC 平面两侧;G 代表乙基链末端甲基的Gauche 取向,即甲基与N 原子位于CCC 平面的同一侧;G′代表当甲基与N 原子位于CCC 平面同侧时的另一取向,即G 与G′取向的甲基分别位于N—C 键两侧.Crocker 等[10]结合红外光谱与拉曼光谱方法发现在固相下三乙胺基态仅存在一种稳定的构象异构体TGG,而在液相下三乙胺基态却存在3 种稳定的构象异构体TGG,TGG′与GGG.Brushweller 等[11]利用MM2 分子力学方法与动态核磁共振谱实验方法识别出三乙胺分子基态的7 种相对稳定的构象异构体.这些构象异构体分别具有C1,Cs与C33 种对称性,其中具有C3对称性的构象异构体G′G′G′的能量最低;具有C1对称性的构象异构体GAG(A 代表甲基的T 取向)的能量次之,仅比G′G′G′高0.01 kcal/mol(0.4 meV);具有Cs对称性的构象异构体GAG′的能量最高,比具有C3对称性的G′G′G′能量高出~0.22 kcal/mol (9.5 meV).进一步地,在97 K温度下测得具有C1与Cs对称性的构象异构体相对占比之和可达94%,但实验上无法区分C1与Cs的占比[11,12].Konaka 等[13]利用气相电子衍射实验技术的方法研究了气相三乙胺基态的构象结构,获得了三乙胺基态构象中三种对称性C1,Cs与C3的布居占比分别为33%,11%与56%.同时,基于MM2 计算方法的结果表明具有C3对称性的构象异构体是最稳定的,这与Brushweller 等[11]的结果一致,但基于4-21G 基组的从头算方法得到的结果却表明具有C1对称性的构象异构体是最稳定的[13].Weber 等[4]利用时间分辨的里德堡电子能谱方法并结合量化计算方法探测到气相三乙胺电子激发态具有三种构象异构体R1,R2与R3,并推测三乙胺基态可能存在4 种能量最低的构象异构体G1,G2,G3与G4.然而,该研究没有给出基态的4 种构象异构体的具体的分子结构参数与红外振动光谱.综上所述,目前对于三乙胺基态的稳定的构象异构体的数量、结构、能量及红外光谱等均未形成统一的认知与理解,需要利用更多先进的实验技术与更高精度的理论计算来阐明三乙胺的分子构象结构与红外光谱.
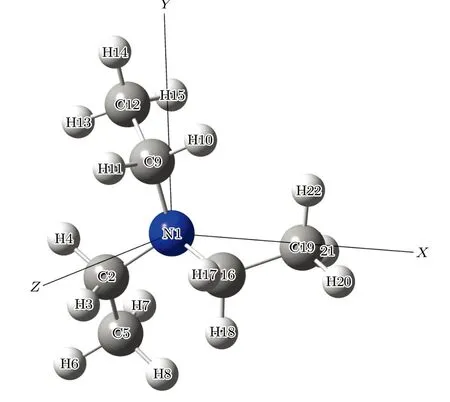
图1 三乙胺分子在笛卡尔坐标系下的结构示意图.Fig.1.Schematic structure of triethylamine in Cartesian coordinate system.
本工作利用密度泛函理论在分子构象结构计算方面的优势[14-19],采用杂化密度泛函方法B3LYP 对气相三乙胺基态的不同构象进行全优化,沿二面角φ1(C9N1C2C5)与φ2(C16N1C9C12)构成的二维坐标扫描了—180°—180°范围内构象异构化势能面,甄别出12 种三乙胺基态异构体,详细计算与分析了这些构象异构体中能量较低的6 种构象异构体的结构与能量,并针对4 种构象异构体,比较其红外光谱与特殊的振动模的相似性与差异性.这些研究结果可以为理解三乙胺分子电子激发态结构及动力学机制提供重要的参考信息,也可以为研究更复杂的氨基酸、多肽体系的构象结构与性质提供一定的指导.
2 理论计算方法
本工作的理论计算均在Gaussian09 量子化学计算软件[20]完成.以Konaka 等[21]得到的对称性最低的C1对称性的三乙胺构象异构体(TG′G′)中的三个二面角参数作为基准,利用密度泛函理论的杂化密度泛函方法B3LYP 在6-311++G(d,p)[22]基组水平上对它的分子结构进行优化,获得了其稳定的构象结构.在这个结构基础上,以10°每步的步长,沿二面角φ1(C9N1C2C5)与φ2(C16N1C9C12)构成的二维坐标扫描—180°—180°范围内构象异构化势能面,甄别出12 种稳定的构象异构体,并对它们所具有的对称性与甲基的取向进行了识别与定义.所有构象异构体结构的频率均没有出现虚频,说明优化所得的构型是稳定的.然后,对其中处于势能面能量相对较小区域的6 种构象异构体在B3LYP/6-311++G(d,p)水平上做了结构优化、频率与单点能计算.同时我们对不同异构体都做了零点能修正.为了验证计算的准确性,进一步使用了二阶微扰方法MP2[23]在6-311++G(d,p)基组水平上对它们进行计算并比对其结果.最后,选择了4 种构象异构体G1,G2,G3 与G4,在B3LYP/6-311++G(d,p)水平上进一步计算了它们的红外光谱并获得了这4 种构象异构体的振动模式及其对应的振动频率.根据实验获得的红外光谱,计算所获得的振动频率需要做频率修正,修正因子取0.98.
3 计算结果与讨论
3.1 三乙胺基态的构象结构与势能面
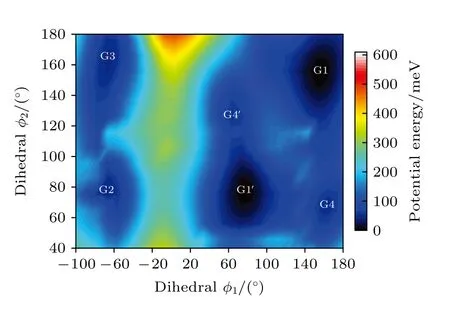
图2 中展示了沿二面角φ1(C9N1C2C5)与φ2(C16N1C9C12)在—180°—180°范围内进行二维扫描所得到的构象异构化势能面.势能面上多个区域显示出较低能量点,表明存在不同的局域构象异构体.根据能量信息,共标记出12 种构象异构体,分别标记为G1,G1′,G2,G3,G4,G4′,G5—G10.将这12 个构象异构体进一步在B3LYP/6-311++G(d,p)水平上做优化、频率与单点能计算,获得的稳定构象结构分别具有C3,C1与Cs对称性.检查所有构象异构体的频率均没有出现虚频,说明优化所得的构型是稳定的.12 种优化后的稳定构象异构体的相应的二面角和能量等结果列于表1 中.由表1 可知,G1 是能量最低,具有最稳定的结构.G2—G9 与G1 之间的能量相差约40—50 meV 左右,而G2—G9 之间的相对能差非常小,这表明它们的稳定性相近.G10 的能量相对G1 要高达118.59 meV,是12 个稳定构象异构体中能量最大的.图2 也反映出G10 位于G8、G9 与G10 构成的局部势能面区域洼地的高处.这12 种构象异构体可绕相应的二面角φ1,φ2与φ3(C2N1C16C19)的单键旋转而相互转化,二面角φ1,φ2与φ3的旋转是引起三乙胺构象变化的主要原因.
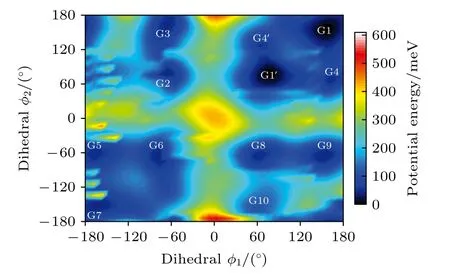
图2 沿二面角φ1(C9N1C2C5)与φ2(C16N1C9C12)构成的二维坐标扫描—180°—180°范围内三乙胺构象异构化势能面Fig.2.The conformational isomerization potential energy surface in the range of—180°—180° scanning along the twodimensional coordinates formed by the dihedral angles of φ1(C9N1C2C5) and φ2 (C16N1C9C12).
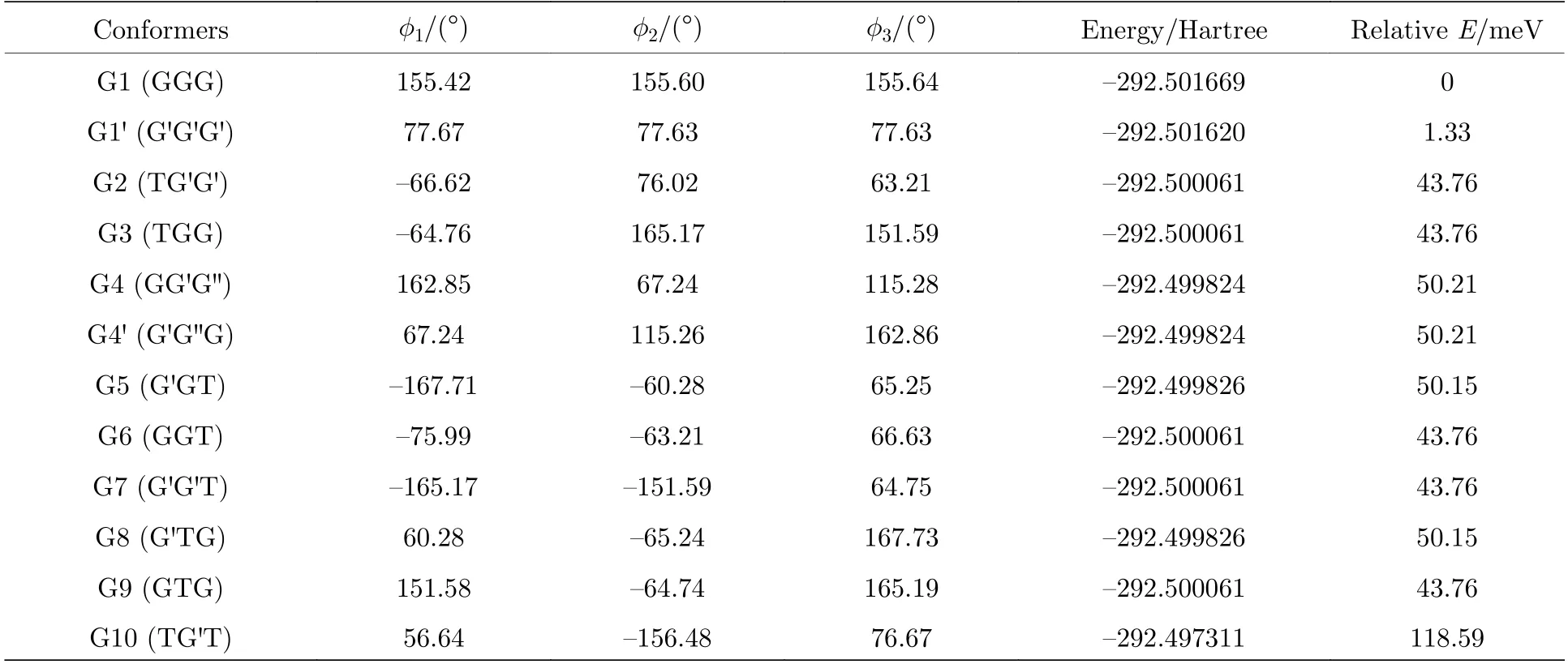
表1 基于B3LYP/6-311++G(d,p)水平计算得到的三乙胺的12 种稳定构象异构体的二面角与能量Table 1.The energies and dihedral angles of the 12 conformers of triethylamine calculated on B3LYP/6-311++G(d,p) level.
在这12 个构象异构体中发现了一种新的甲基取向结构,该甲基基团取向与N1 原子处于C2C9 C16 平面同侧,这与G 和G′取向不同,被命名为G′取向.先前报道的G 与G′取向分别位于N—C键两侧,乙基链与N 原子构成的NCC 平面与C2C9C16 平面不垂直,而G′取向中的NCC 平面则与C2C9C16 平面垂直,这使得G′取向的甲基无法被区分在N—C 键的任意一侧,即C—C 键与N—C 键在分子Z 轴方向上重合.将C5H3,C12H3和C19H3这3 个甲基基团的取向按顺序排列,可以对三乙胺的所有构象异构体的结构进行指认.G1 具有C3对称性,3 个甲基基团C5H3,C12H3和C19H3的取向是相同的,被指认为GGG 构象.而G2 具有C1对称性,C5H3甲基基团与N1 原子分别位于C2C9C16 平面的两侧(T 取向),C12H3与C19H3甲基基团均与N1 原子位于C2C9C16平面同侧,并且C12H3与C19H3甲基基团的取向与G1 中甲基的取向不同,它们分别位于NCC 平面两侧,即为G′取向,因此G2 被指认为TG′G′构象.G4 与G4′两种构象异构体甲基均与N1 原子处于C2C9C16 平面同侧,但由于G4 与G4′具有G′与G′这两种不同的甲基取向,所以并不具有G1与G1′所具有的C3对称性,而是具有Cs对称性.其他构象异构体的命名详见图3.
从图3 可见,12 种稳定构象异构体中的N1 原子与C2C9C16 构成的平面形成四面体形状,其中N1—C2,N1—C9 或N1—C16 键长的平均值在1.4680 Å左右,∠C2N1C9 或∠C9N1C16 或∠C2 N1C16 键角的平均值在111.98°左右,使得三乙胺分子具有类似于NH3分子构型的稳定结构,具体参数见表1.三乙胺分子内甲基基团之间因为彼此接近会在空间上产生相互阻碍的作用,产生的空间位阻效应.二面角φ1,φ2与φ3的旋转可以表征出三乙胺3 个甲基基团C5H3,C12H3与C19H3的相对空间位置.当空间位阻相对较小的时候,相对稳定的3 个甲基的取向反映在二面角φ1,φ2与φ3的大小.
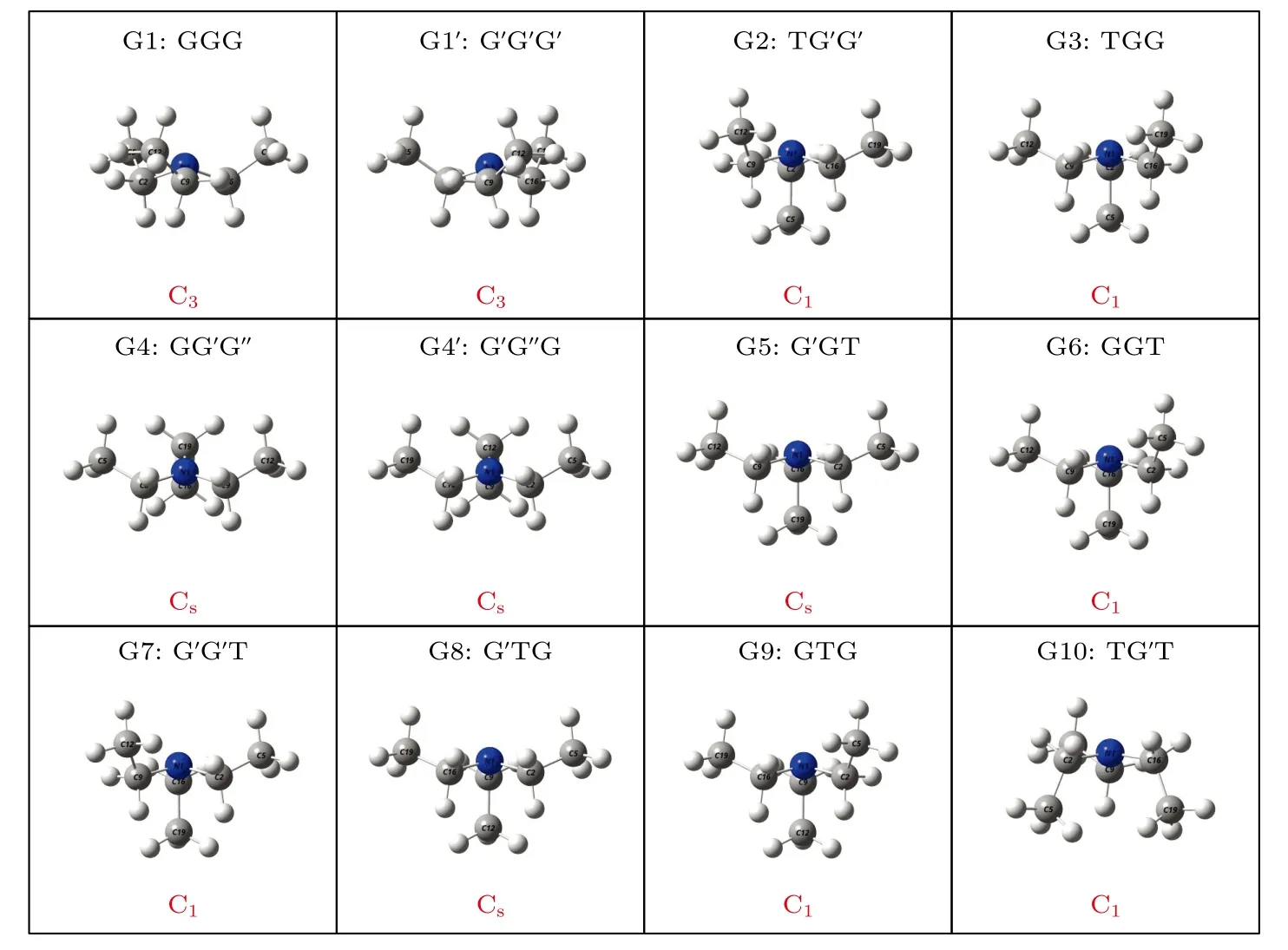
图3 基于B3LYP/6-311++G(d,p)水平计算得到的三乙胺的12 种稳定构象异构体的分子结构Fig.3.The 12 stable conformers of triethylamine calculated on B3LYP/6-311++G(d,p) level.
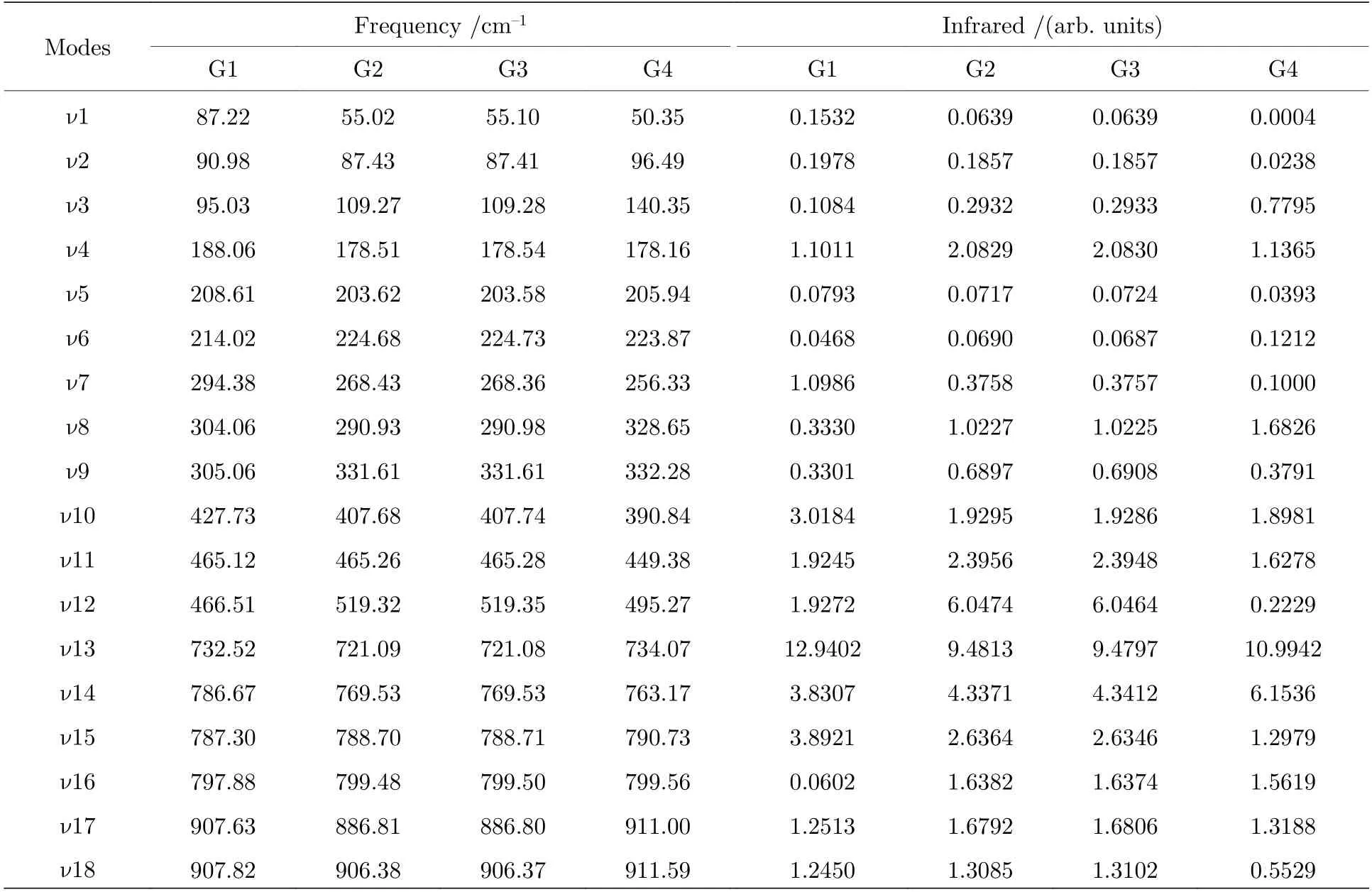
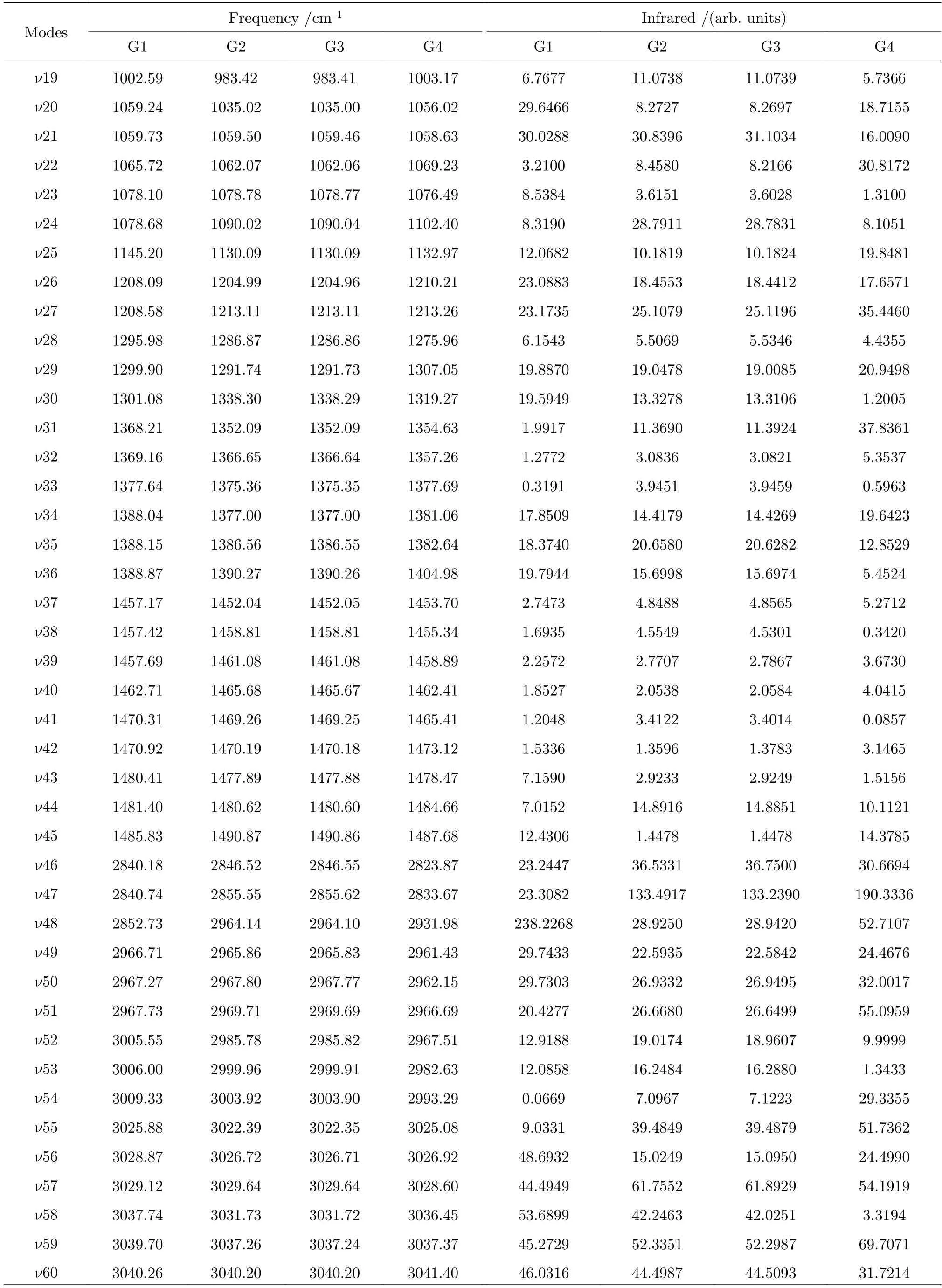
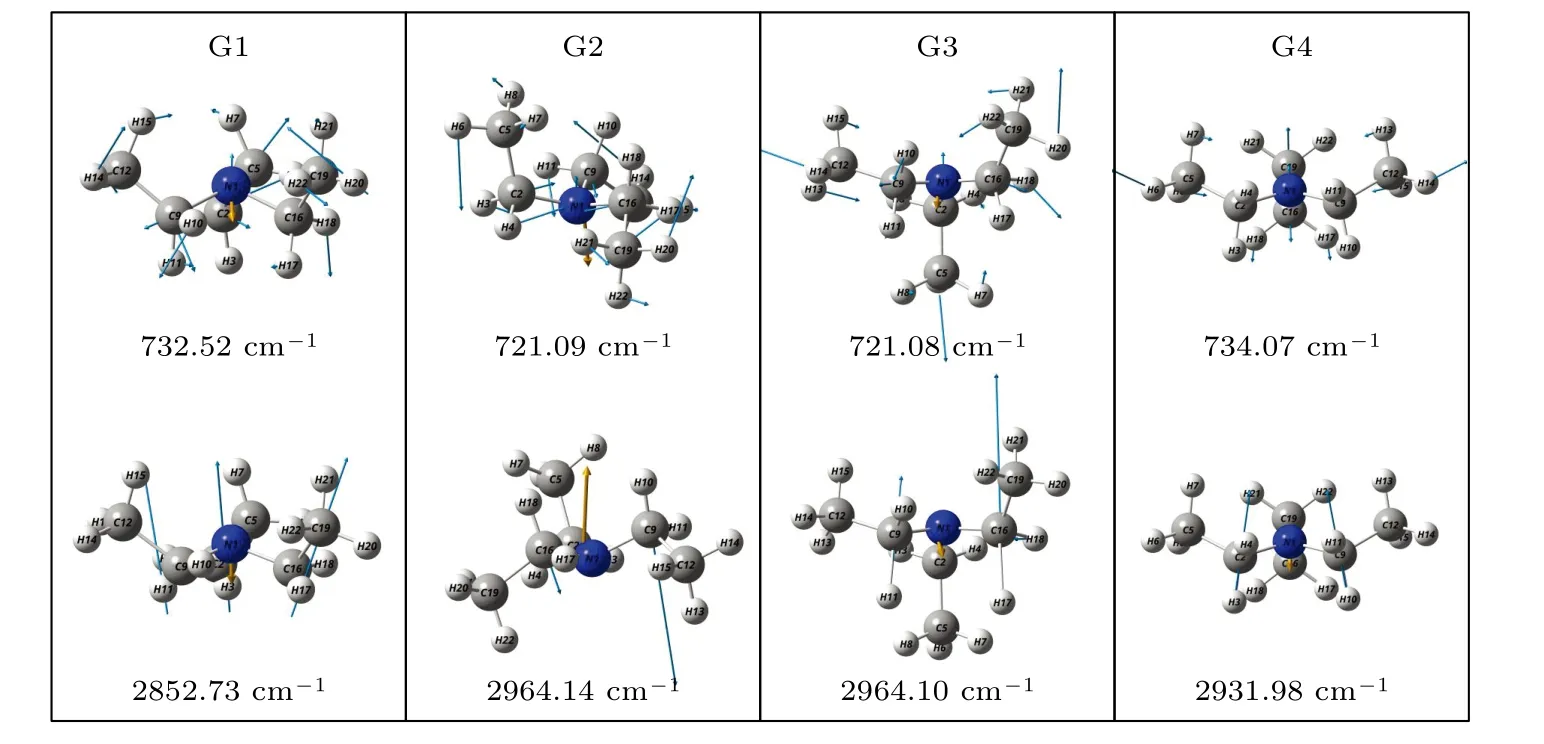
基于从头算方法指出具有C1对称性的构象异构体最稳定[13].而在B3LYP/6-311++G(d,p)水平上,计算结果表明G1 能量最低,是最稳定结构,这与Konaka 等[13]利用MM2 方法计算的结果一致.为了进一步验证计算方法对分子构象结构优化、频率、单点能造成的影响,对图2 中势能面的能量较低区域的6 种构象异构体(G1,G1′,G2,G3,G4 与G4′),如图4 所示,在MP2/6-311++G(d,p)水平上分别进一步做了结构优化、频率与单点能计算.获得G1,G1′,G2,G3,G4 与G4′的二面角参数和能量列于表2 中.相对于MP2 方法,在B3LYP水平下获得的6 种构象异构体的能量更小,其中G1 与G1′之间的能量差仅为1.33 meV,而G2 与G3,G4 与G4′之间的能量则无法区分.在MP2/6-311++G(d,p)计算下的G1 与G1′之间的能量无法区分,而G2 与G3,G4 与G4′之间的能量存在较小的差别.这些计算结果表明6 种构象异构体的能量次序为G1/G1′ 表2 三乙胺的6 种稳定构象异构体在MP2/6-311++G(d,p)计算下的二面角与能量Table 2.The energies and dihedral angles of the six stable conformers of triethylamine on the level of MP2/6-311++G(d,p). 图4 φ1 (—100°—180°)与φ2 (40°—180°)范围内的6 种构象异构体的势能面Fig.4.The conformational isomerization potential energy surface of the six conformers in φ1(—100°—180°) and φ2(40°—180°). G1 的二面角φ1,φ2与φ3分别为155.42°,155.60°与155.64°,而G1′的二面角φ1,φ2与φ3分别为77.67°,77.63°与77.63°.如图3 所示,G1 与G1′的构象结构非常相似,均具有C3对称性,G1为GGG 构象,G1′为G′G′G′构象.G1 与G1′的主要区别在于3 个甲基C5H3,C12H3与C19H3的相对空间取向不同,这种细微的结构差异导致G1 与G1′的能量差非常小,如前所述,基于B3LYP 的能量差仅为1.33 meV,而基于MP2 的结果则无法区分.在已报道的研究中[4,9-13],G1 构象异构体均未被识别出,而是认为仅存在G1′.在B3LYP和MP2 方法下,G4 与G4′的能量比G1 与G1′的能量分别高出~50 meV 和33 meV.此外,G4 与G4′的能量差在B3LYP 方法下为0,在MP2 方法下约为0.03 meV.G4 的二面角φ1,φ2与φ3分别为162.85°,67.24°与115.28°,而G4′的二面角φ1,φ2与φ3分别为67.24°,115.26°与162.86°,如图3所示.其中G4′构象异构体在已报道的研究[4,9-13]中也未被识别出.通常而言,三乙胺的三条乙基链可以被认为是等价的,由表1 中可以知,拥有相同3 个甲基取向的构象异构体之间的能量几乎相同.G2(TG′G′),G3(TGG),G6(GGT)和G7(G′G′T)的能量均为43.76 meV,G5(G′GT)与G8(G′TG)的能量均为50.18 meV 等.但在本工作中,这些构象异构体处于势能面上不同二面角坐标的势阱中,认为是不同的构型.G2,G3,G6 和G7 具有C1对称性,在B3LPY 方法下4 个构型能量差为0,在MP2方法下G2 和G3 能差仅为0.11 meV.这些结构无法通过能量的差异性进行区分.考虑到G1 与G1′,G4 与G4′两组构象结构的差异性非常小,另外,G2 与G3 构象在能量上也无法区分.因此,进一步通过B3LYP/6-311++G(d,p)计算对构象异构体G1—G4 进行红外光谱的分析并比对其结果. 在B3LYP/6-311++G(d,p)基础上进一步计算了4 种构象异构体G1,G2,G3 与G4 的红外光谱,如图5 所示.G1—G4 的红外光谱显示在2800—3300 cm—1范围内均存在较强的吸收,而在0—1600 cm—1范围内的吸收较弱,这与NIST 气相实验获得的红外光谱相似.相应的G1—G4 的振动频率列于表3 之中,分析发现,相对于能量最小的G1 构象异构体而言,G1—G4 的各种振动模式的频率发生少量移动,平均移动量小于20 cm—1,这主要是由于构象异构体中的甲基取向不同导致原子在振动过程中极化率的变化不同而引起的.特别地,G2(TG′G′)与G3(TGG)具有相同的C1对称性但具有不同的甲基取向,它们的红外光谱却非常相似. 表3 基于B3LYP/6-311++G(d,p)水平计算得到的G1—G4 构象异构体的振动模式与频率Table 3.The vibrational modes and their frequencies of the G1-G4 conformers calculated on B3LYP/6-311++G(d,p) level. 表3 (续)基于B3LYP/6-311++G(d,p)水平计算得到的G1—G4 构象异构体的振动模式与频率Table 3 (continued).The vibrational modes and their frequencies of the G1-G4 conformers calculated on B3LYP/6-311++G(d,p) level 图5 在B3LYP/6-311++G(d,p)水平上计算得到的G1—G4 构象异构体的红外光谱Fig.5.The infrared spectra of the G1—G4 conformers calculated at B3LYP/6-311++G(d,p) level. 对于4 种构象异构体,观察到2800—3300 cm—1范围内存在多个振动谱峰,主要归属为C-H 的振动.G1 中最强的峰位于2852 cm—1,对应C2—H3,C9—H11 与C16—H17 的对称伸缩振动;3027 cm—1,对应C5 或C12 所在甲基上H 原子的非对称伸缩振动;3028 cm—1,对应C5,C12,C19 所在甲基上H 原子的对称伸缩振动;3037 cm—1,对应C5,C12,C19 所在甲基上H 原子的非对称伸缩振动.对于0—1600 cm—1范围内的振动峰,其强度比2800—3300 cm—1范围内的振动峰的强度要弱很多,主要归属为乙基的各种振动模式或乙基的各种振动模式伴随着N 的骨架振动.例如,732 cm—1,对应N1与 C2,C9,C16 骨架的伞状振动模,即N1 与 C2,C9,C16 骨架的对称弯曲振动,并伴随着乙基的摇摆振动.与NH3分子类似,当位于N1 原子上的孤对电子被激发形成里德堡电子态3p 后,三乙胺分子上的N1 原子与C2,C9 与C16 构成的骨架会发生平面化运动,即三乙胺的伞状振动模会被激发,该伞状振动模对三乙胺分子的激发态构象异构动力学过程的理解极为关键.此外,427 cm—1,对应N1 与 C2,C9,C16 构成的骨架的对称伸缩振动,并伴随着乙基的摇摆振动. 图6 展示了最强的C—H 伸缩振动模与伞状振动模,图中原子键轴处的箭头表示跃迁偶极矩的单位矢量,各原子处的箭头表示对应原子的位移矢量. 图6 基于B3LYP/6-311++G(d,p)水平计算得到的G1—G4 构象异构体的伞形振动(上排图)和C—H 对称伸缩振动(下排图)及其频率Fig.6.The umbrella vibration mode (upper panel) and C—H symmetric stretch mode (lower panel) and their frequencies of the G1—G4 conformers calculated on B3LYP/6-311++G(d,p) level. 基于密度泛函理论,采用B3LYP 泛函在6-311++G(d,p)基组上计算了气相三乙胺基态的稳定构象结构、频率、能量及红外光谱.通过扫描构象转化相关的二维构象势能面,共甄别出12 种稳定的构象异构体,并结合MP2/6-311++G(d,p)计算方法进一步确定出其中具有不同对称性的构象异构体之间的能量次序,证实最稳定的构象异构体为具有C3对称性的G1 与G1′.与已报道的研究结果相比,识别出一种新的C3对称性的构象异构体G1 (GGG),其二面角φ1,φ2与φ3分别为155.42°,155.60°与155.64°.同时识别出1 种新的甲基取向G′,以此标定出2 种新的构象异构体G4 (GG′G′)与G4′ (G′G′G).计算获得这2 种结构的二面角φ1,φ2与φ3分别为162.85°,67.24°,115.28° 和67.24°,115.26°,162.86°.基于不同方法计算的结果,分析发现G1/G1′,G2/G3,G4/G4′的能量近乎相等.进一步在B3LYP/6-311++G(d,p)水平上计算了G1,G2,G3 与G4 构象异构体的红外光谱,结果表明G1—G4 的红外光谱在0—1600 cm—1范围内的强度较弱,而在2800—3300 cm—1范围内的强度较强,标定出伞状振动模与最强的C—H 伸缩振动模等特征振动模.G1—G4 的各种振动模式的频率会因为构象的不同而发生移动,平均移动量小于20 cm—1.本工作详细揭示出三乙胺基态的分子构象异构体的结构、能量、红外振动光谱等信息,为理解三乙胺分子电子激发态的结构及动力学机制提供重要的参考信息与指导.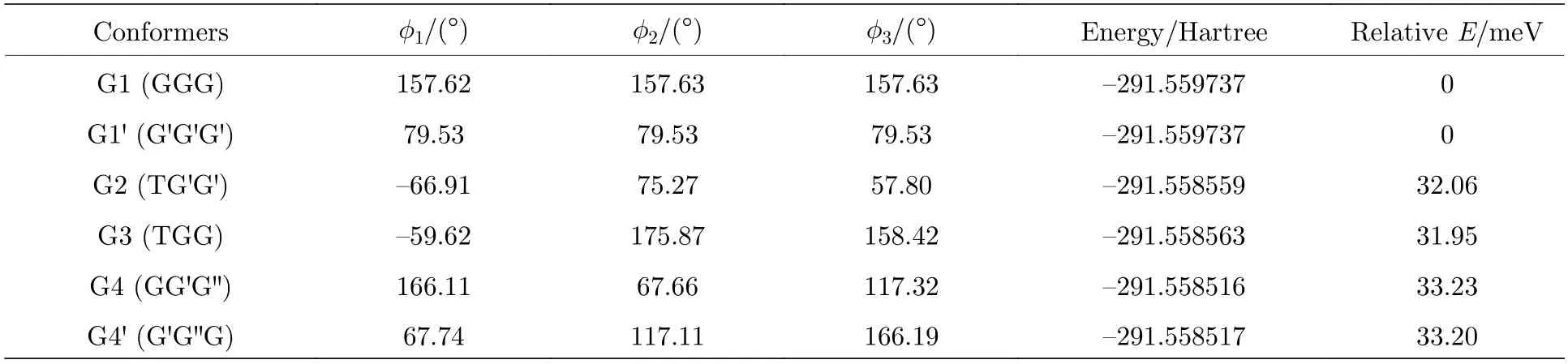
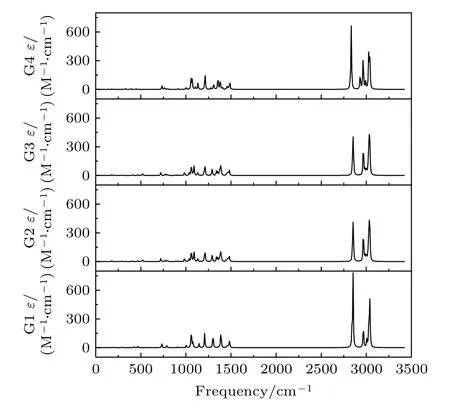
3.2 三乙胺基态稳定构象异构体的红外光谱
4 结论

