基于Nyström 柯西核共轭梯度算法的混沌时间序列预测*

齐乐天 王世元† 沈明琳 黄刚毅

1) (西南大学电子信息工程学院,重庆 400715)

2) (非线性电路与智能信息处理重庆市重点实验室,重庆 400715)

混沌时间序列能够较好反映真实环境的非线性和非平稳性特性,然而具有二阶统计特性的核自适应滤波器(kernel adaptive filter,KAF)在处理含噪声和异常值的混沌时间序列时,其预测性能显著下降.为提高核自适应滤波器的鲁棒性,本文提出了一种用于测量非线性相似度的柯西核损失(Cauchy kernel loss,CKL),并采用半平方(half-quadratic,HQ)方法保证了CKL 的全局凸性.为改善随机梯度下降法收敛速度较慢且容易陷入局部最优的不足,采用共轭梯度(conjugate gradient,CG)方法优化CKL.进一步,为解决核矩阵网络增长的问题,采取Nyström 稀疏策略近似核矩阵,并利用概率密度秩量化(probability density rank-based quantization,PRQ)提高逼近精度.基于此,本文提出了一种新的基于Nyström 和PRQ 的柯西核共轭梯度(Nyström Cauchy kernel conjugate gradient with PRQ,NCKCG-PRQ)算法有效实现了混沌时间序列的预测.基于合成和真实两类混沌时间序列验证了所提NCKCG-PRQ 算法在稳态性能,鲁棒性和计算存储复杂度上的优势.

1 引言

混沌现象[1]作为一种类似随机的无规律行为,是由不附加随机因素的确定性非线性动力学系统产生.由于现实环境常具有非线性和非平稳性,故混沌系统在很大程度上能够重构现实世界的非线性系统.然而,混沌系统对初始值的敏感特性使得其长期行为不可精准预测;而混沌吸引子的确定性动力学机制使得混沌时间序列具有较为准确的短期预测性[2].因此,混沌时间序列的有效预测是重构混沌系统的基础,具有重要的实际意义和挑战性;精准的预测方法能够被广泛应用于保密通信、情感学习、电力系统短期负荷预测、天气预测[3-4]等领域.然而,在实际应用中,混沌信号常受到不同程度的噪声干扰,因此如何最大限度地在各类噪声环境下实现混沌序列的精准预测,已经成为混沌信号处理的研究热点.混沌时间序列的预测方法可分为全局预测法[5]、局部预测法[6]和自适应预测法[7].其中,全局预测法采用全部样本数据拟合非线性函数,但当样本数据量大时运算速度较慢[8-9];局部预测法因仅利用部分数据用于预测,运算速度较快但预测精度较低[10-11].作为一种全局预测法以及局部预测法的扩展,自适应预测法将自适应滤波算法融合于前两类方法中[12-13].相比于经典的局部预测法和全局预测法,自适应预测法因其参数配置简单、混沌运动轨迹的自适应跟踪特性、良好的去噪特性、以及在小数据量前提下仍具备较高的预测精度等诸多优点,已在现实环境中得到广泛应用[14].因能够根据混沌序列的变化自动调整模型参数的特性,自适应预测法为混沌时间序列预测提供了一种新的思路,但因采用的自适应滤波算法收敛速度不够快限制了其在实际应用的实时性.

考虑到现实环境中的数据常具有非线性特征,使得基于线性结构的自适应滤波系统在处理非线性问题时存在局限性.为此,核方法(kernel method)将输入信号非线性映射到高维再生核希尔伯特空间中,然后在特征空间中执行线性滤波,发展出了核自适应滤波(kernel adaptive filter,KAF),如基于均方误差(mean square error,MSE)和最小二乘(least squares,LS)准则的核最小均方算法[15]和核递归最小二乘算法[16].在自适应滤波算法中,代价函数,权重更新方式和稀疏策略决定了混沌时间序列预测性能.

优化方法是KAF 算法中权向量更新的关键.从本质上讲,优化方法的选取决定了算法的计算复杂程度和收敛速度.随机梯度下降(stochastic gradient descent,SGD) [22]法因其简单,在KAF得到广泛应用.然而,基于SGD 的滤波算法通常容易陷入局部最优,导致性能下降.作为SGD 方法的延拓,牛顿法和共轭梯度法(conjugate gradient,CG)[23]能更好地求解误差函数.但是,在牛顿法中需要保证海森矩阵(Hessian matrix)的正定性并计算海森矩阵的逆,这在一定程度上增加了计算复杂度,限制了其实际应用[24].CG 法能够平衡收敛速度和计算复杂度.与SGD 法相比,CG 法不仅提高了算法收敛速度,并且在计算复杂度较低的情况下取得了与递归算法相当的性能[23].但是,相比于牛顿法,CG 法因不需要计算海森矩阵的逆,所以能够获得更加稳定的解.

通常,KAF 采用高斯核实现在线学习,即根据每一个新输入的数据对系统参数进行学习.然而,大规模的数据导致网络尺寸线性增长,增加了计算量和空间存储,这对KAF 的在线实际应用提出了巨大挑战.抑制KAF 网络增长的方法主要包括量化[25]和稀疏化策略.但是,量化和稀疏化策略均不能预先设定网络结构大小,用以满足特定计算和存储要求.Nyström 方法采用近似法重构矩阵[26],将高维度问题转化为低维度空间,通过固定维网络结构来逼近KAF 中的核矩阵,并在逼近精度和计算复杂度两方面实现了平衡.然而,Nyström 方法中常采取的抽样策略是随机抽样[27]和k-均值抽样[28].由于两种抽样方法具有对初始样本选择的敏感性,所以其逼近精度通常无法达到预期效果.基于此,提出了基于概率密度秩的量化(probability density rank-based quantization,PRQ)[29]采样方法进一步提高近似精度.

受启发于半平方(half-quadratic,HQ) [24]方法转化CKL 后代价函数的全局凸性和鲁棒性,本文根据混沌时间序列的短期可预测性,在CG 优化方法上引入了基于PRQ 采样的Nyström 方法,提出了一种新的基于PRQ 采样的Nyström 柯西核共轭梯度 (Cauchy kernel conjugate gradient,CKCG)算法(NCKCG-PRQ).所提的NCKCG-PRQ 算法在预测麦克格拉斯(Mackey-Glass,MG)混沌时间序列和实际电路采集的蔡氏混沌时间序列的两类实例中,展现了在非高斯噪声环境下预测性能的强鲁棒性、低稳态误差及低计算复杂度的特点.

2 背景介绍

本节首先介绍柯西核代价函数,接着采用HQ方法将柯西核函数转化为具有二次型形式的全局凸函数,最后采用Nyström 法对矩阵进行有效重构.

2.1 柯西核代价函数

显然,柯西核函数不是一个全局凸函数.

2.2 半平方法转化柯西核函数

由于 (3)式的海森矩阵只有在满足一定条件时才是正定的,因此不能始终保证其全局凸性,这就限制了柯西核函数在解决凸优化问题中的应用.实际上,柯西核函数可以看作一个由具有对数函数形式的柯西函数和指数函数形式的相关熵函数映射而来的复合函数,借助两次半平方优化法使柯西核函数转化为全局凸函数.因转化后的数学表达式为二次型形式,所以能够有效解决凸优化和共轭梯度优化的问题.

对于应收账款的估价，一般来说，有三种方法：成本法、市场法和收益法。成本法与市场法不能适应应收账款的市场需求。对于收益法，一条原理指出：资产的价值等于它将来给所有者带来的经济利益的净现值。而应收账款作为一种债权，未来会给其所有者带来经济利益，故采用收益法。因此，选择正确的资产估价方法，是应收账款证券化能否交易成功的关键。

此时,(2)式中求解柯西核函数的最优解问题等价于求解如下问题:

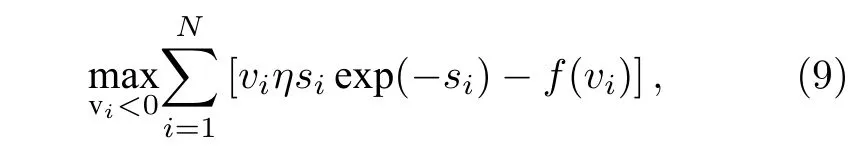
其中,viηsiexp(−si)−f(vi) 是关于vi独立函数.(9)式的求解可以通过交替优化方法实现.借助 (8)式可以解得vi的解析解是vi=−[1+ηsiexp(−si)]−1,其中vi是一个负数.给定vi,(9)式的优化问题等价于如下形式:

不难看出,(11)式是一个全局凸函数且其中包含了共轭梯度优化方法所需要的二次型形式.(11)式中加权最小二乘问题的海森矩阵如下:

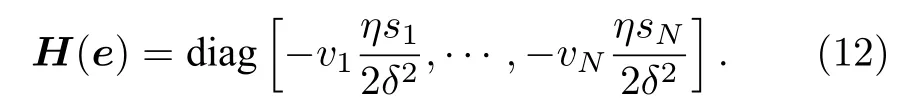
由于vi小于0 且ηsi大于0,所以海森矩阵是正定的,保证了全局凸性.(11)式的解可通过半二次方法求解加权最小二乘问题得到.由此可知,半平方法对柯西核函数的转化打破了海森矩阵中参数δ和η关于误差e的限制条件,进一步促进了柯西核函数在凸优化问题中的应用.

2.3 Nyström 方法

将原始输入u(i) 映射到再生核希尔伯特空间中,可得输入φ(u(i)) 的数据矩阵Φ ∈RD×n为

因此,采用Nyström 方法生成固定维数为m的特征空间,可有效降低计算和空间复杂度.

3 基于PRQ 采样的Nyström 柯西核共轭梯度

3.1 在线NCKCG 算法

在自适应滤波预测的在线学习中,根据特征空间中变换后的输入z(uk),将非线性系统表示为

则残差向量的递归形式为:

最后,结合 (20)—(27)式,得到NCKCG 算法.

3.2 概率密度秩的量化采样

在Nyström 稀疏策略[29]中,采样方法的选取对矩阵近似起着至关重要的作用,将直接影响低秩矩阵的近似精度.直接选取任意m列训练数据重构的低维矩阵可能在很大程度上不能反映数据集的整体特征,在数据存在有大异常值情况下,随机采样方法并不能获得预期的近似精度.此外,k-均值采样法采用预先设定的阈值距离来获取迭代所对应的样本点,容易选取少数无效的边界值或离群值,降低了近似精度.为了保证近似精度,采用PRQ的自适应采样法,选择信息量更大的列,使得所选数据包含更多的有效信息.PRQ 采样通过将原始数据替换为对应聚类中的地标点,有效避免了随机采样和k-均值采样均存在的初始点选取问题.

表1 NCKCG-PRQ 算法Table 1.NCKCG-PRQ algorithm.

4 仿真结果及分析

为验证本文所提NCKCG-PRQ 算法在混沌时间序列预测的有效性,选择两类混沌时间序列,即数值仿真的MG 混沌时间序列[34]和由真实蔡氏电路产生的混沌时间序列[31].

4.1 仿真实验模型

4.1.1 混沌时间序列模型

MG 混沌时间序列因其具有周期性和混沌动力学特性,被广泛地应用于非线性系统建模.因此,考虑使用这个例子来验证本文所提出的NCKCGPRQ 算法在非高斯噪声环境下的优越性.MG 混沌时间序列由下式产生:

式中,时滞参数τ影响了系统的混沌特性.τ大于17 时,系统呈现混沌,且其值越大,混沌程度越高,本文τ设置为30.在采样周期为6 s 时,对时间序列进行离散化.为实现混沌时间序列的预测,选取之前的7 个样本点 [st−1,st−2,···,st−7] 预测当前值st.

4.1.2 蔡氏混沌时间序列模型

蔡氏电路可以产生一个现实存在的混沌时间序列.为获取真实世界的混沌时间序列,建立了如图1 所示的电路系统.电源模块将220 V 电压转换为12 V 电压用于蔡氏电路.系统搭建中主要采用LM358 运放,100 nF 和10 nF 各一个以及功率直插电感20 mH,详细的电路原理图如图2 所示.

选取图2 中电容C2之间的电压值作为蔡氏混沌时间序列,即图1 中示波器的绿色波形所示.在此次仿真实验中,预测C2之间的电压值并将其标准化为 0—0.1 用以保证实验预测精度.之前最近的5个电压值被用作输入来预测当前的电压值.

图1 示波器示意图Fig.1.Schematic diagram of oscilloscope.

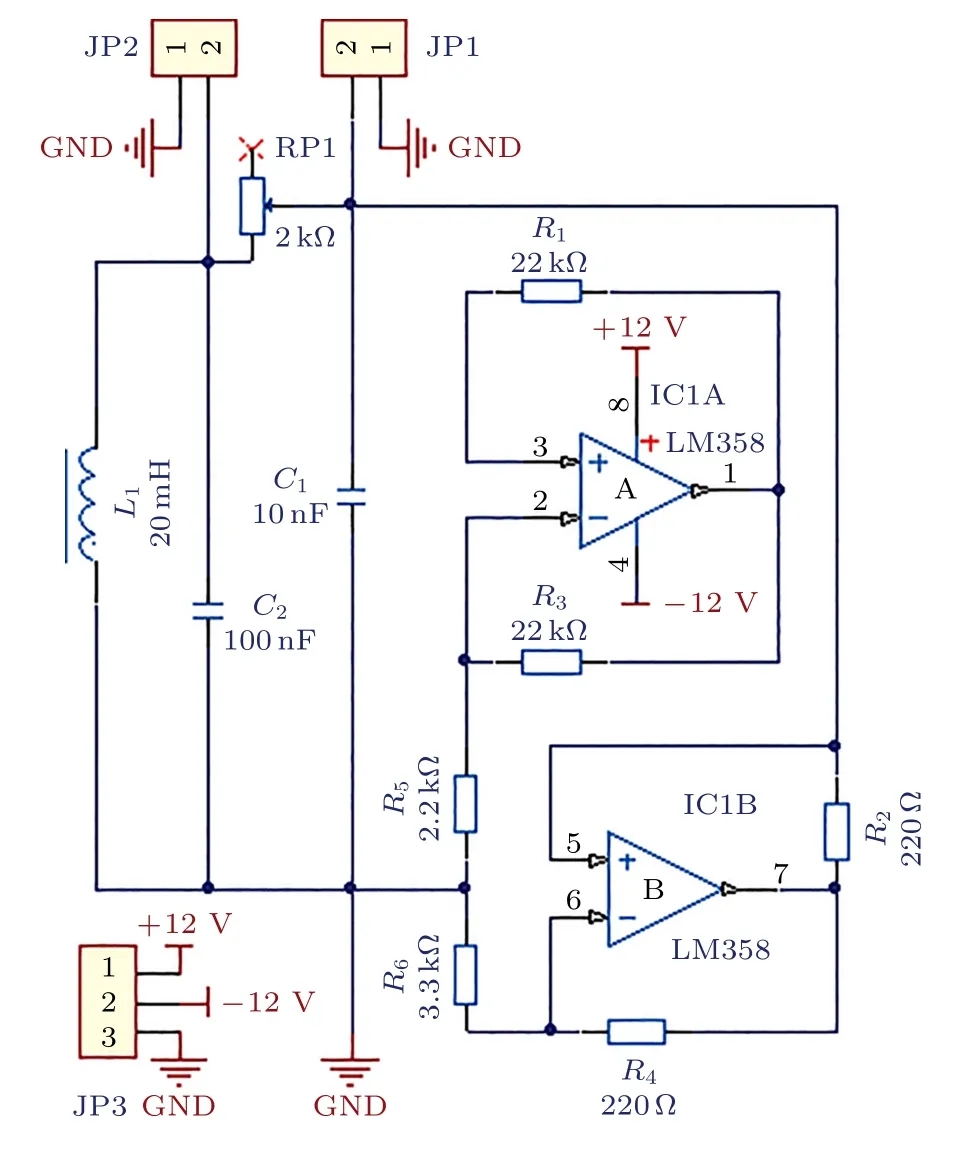
图2 蔡氏电路原理图Fig.2.Schematic diagram of the Chua’s circuit.

4.2 噪声环境

为了验证算法在非高斯环境下的鲁棒性,采用如下的混合高斯噪声模型,即:

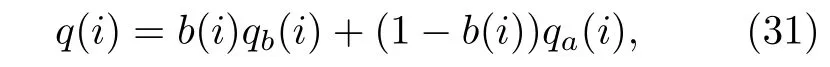
噪声模型中,qa(i) 是零均值且方差为=0.0016的高斯噪声;qb(i) 是用于建模脉冲噪声的α-stable分布[35],其参数为Vα−stable(0.8,0,0.1,0) ;b(i) 是伯努利二项分布发生的概率,P r{b(i)=1}=c且Pr{b(i)=0}=1−c,仿真中选取c=0.1.在仿真实验中一个包含2000 个样本点的数据集添加非高斯噪声后用作训练,另外干净的200 个样本点用作测试,并另选200 个样本点用于Nyström 近似.为了比较预测精度,测试采用如下所示的MSE(单位为dB):

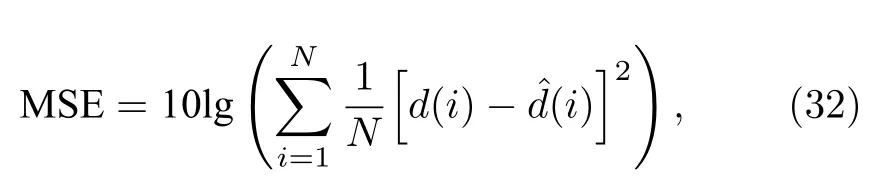
4.3 仿真结果及分析

图3 所示为不同采样点个数 对NCKCG-PRQ算法的稳态MSE 值和平均运算时间的影响.从图3(a)可以看出:1)平均运算时间随m的增大而延长;2) NCKCG-PRQ 算法滤波精度可以通过增大m的方法在一定程度上提高,当m为80 时,其滤波精度趋于稳定;3)m维数越大,滤波精度越高,但计算时间越长.当m为60 时,运算时间约为1.5 s;而当m为80 时,运算时间约为2.5 s.当m从60 增至80 时,滤波精度提高所带来的优势不及运算时间增加带来的计算负担.因此,综合滤波精度和计算时间两方面,在MG 混沌时间序列仿真中将采样点设置为60.为公平起见,所有参与比较的稀疏算法的采样点个数均设置为60.从图3(b)可以看出,随着m增大,滤波精度先增大而后减小,但运算时间是一直延长的.在m=13 时,滤波精度达到最高.因此,同时考虑滤波精度和运算时间两方面,在蔡氏混沌时间序列仿真中最优的采样点个数为13.故参与比较的稀疏算法采样点数目也同样设置为13.

图3 不同采样点个数 m 对NCKCG-PRQ 算法的稳态MSE 值和平均运算时间的影响 (a) MG 混沌时间序列;(b) 蔡氏混沌时间序列Fig.3.Influence of different number of sampling points on steady-state MSE value and average operation time of NCKCG-PRQ algorithm:(a) MG chaotic time series;(b)chaotic time series based on Chua’s circuit.

比较算法包含CKCG[30]算法,随机傅里叶特征柯西共轭梯度(random Fourier features Cauchy conjugate gradient,RFFCCG)[36]算法,Nyström核递归广义最大相关熵 (Nyström kernel recursive generalized maximum correntropy with PRQ sampling,NKRGMC-PRQ)[29]算法,Nyström 核共轭梯度 (Nyström kernel conjugate gradient based on k-means sampling,NKCG-KM)[28]算 法.其中,CKCG 算法是采用具有鲁棒特性的柯西核函数作为代价函数,通过CG 有效优化该代价函数,但随着输入数据的不断加入,核矩阵规模不断增大,计算存储负担加重.CKCG 算法因其鲁棒性强、滤波精度高和运算时间长的特点,是未经过稀疏处理的典型代表.RFFCCG 算法是采用鲁棒柯西函数作为代价函数,通过CG 方法优化该代价函数,利用随机傅里叶特征和均匀随机数来近似核函数,因此具备低计算复杂度且与传统核算法相当的性能,是固定维度稀疏算法的代表.NKRGMCPRQ 算法采用信息论学习(information theoretic learning,ITL)准则中广泛采用的广义最大相关熵准则作为代价函数,通过经典的递归更新方式、基于Nyström 低秩近似的核矩阵以及PRQ 采样方法进一步提高了滤波精度.NKCG-KM 因采用传统二阶误差准则作为代价函数在非高斯环境下不具备鲁棒性.因此,为了全面体现所提NCKCGPRQ 算法的优越性,本文是从代价函数的鲁棒性、优化方法、稀疏策略以及采样方法选择比较算法.为了体现比较的公平性,对所有参与比较的算法参数进行设置,使其都达到理想的滤波精度.

算法的学习曲线和具体的参数选择如图4 所示.其中,σ=0.5 是CKCG 中柯西核代价函数的核带宽,λ=0.25 是柯西核函数参数;α=2 和σ=0.6 是NKRGMC-PRQ 参数;γ=0.3 为RFFCCG中柯西代价函数参数;λ=0.999 是NKCG-KM 算法遗忘因子;δ=0.5 和η=0.25 是NCKCG-PRQ算法柯西核代价函数参数.

各个算法的平均字典个数大小(即采样点数目),平均计算时间和稳态MSE 的详细仿真结果如表2 和表3 所示.从图4 可以看出,由于脉冲噪声的存在,NKCG-KM 算法的性能出现发散,由此可知基于二阶统计测度的算法在脉冲噪声下不具备鲁棒性.利用柯西损失来惩罚噪声项,使基于柯西核代价函数的NCKCG-PRQ 算法对非高斯噪声,特别是重尾噪声有很好的抑制效果.从表2 和表3可知,与稀疏算法NKRGMC-PRQ 和RFFCCG相比,从稳态MSE 角度比较,所提的NCKCG-PRQ算法具有最好的滤波精度;从运算时间角度比较,所提的NCKCG-PRQ 算法具有最短的运算时间.NCKCG-PRQ 算法在低计算复杂度下最大程度逼近了高计算复杂度CKCG 算法的滤波精度.图5是显示了测试集中验证所提算法的预测结果,其中,纵坐标已作归一化处理.从图5 可知,在合成数据的MG 混沌时间序列中所提算法在该仿真实验中能够有效地实现混沌序列的预测;在真实采集的蔡氏电路混沌时间序列中,所提算法基本实现了真实值和预测的输出值的拟合.由此可知,无论是在仿真的MG 混沌时间序列还是真实蔡氏电路产生的混沌时间序列,所提的NCKCG-PRQ 算法在鲁棒性,稳态性能和计算复杂度上均具有较大的优势.

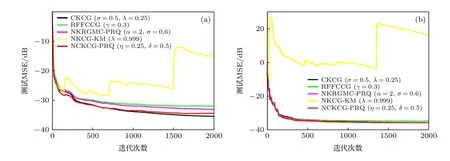
图4 在脉冲噪声环境下不同算法的测试MSE 学习曲线 (a) MG 时间序列 ;(b)蔡氏混沌时间序列Fig.4.Testing MSE learning curves of different algorithms in impulsive noise environment:(a) MG chaotic time series;(b) chaotic time series based on Chua’s circuit.

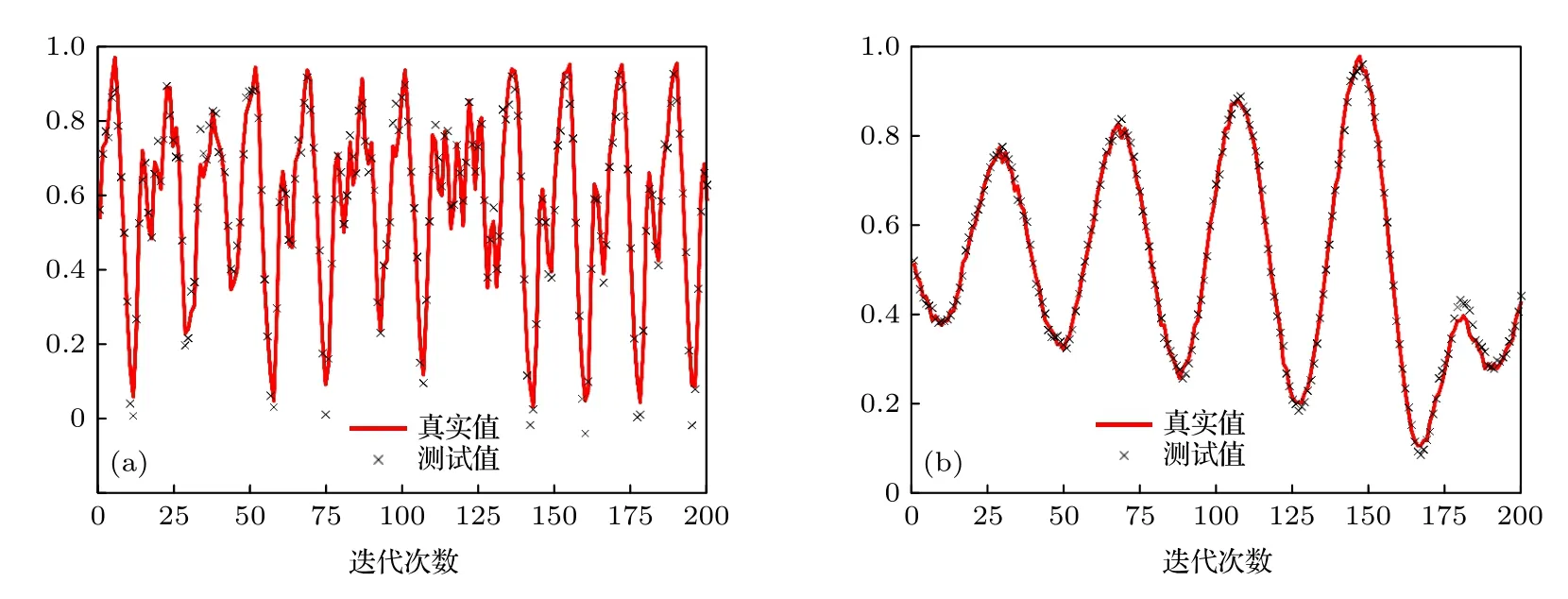
图5 NCKCG-PRQ 算法对测试数据的最终预测结果 (a) MG 混沌时间序列;(b) 蔡氏混沌时间序列Fig.5.Final predicted results of NCKCG-PRQ algorithm for the test sets:(a) MG chaotic time series;(b) chaotic time series based on Chua’s circuit.

表2 不同算法在MG 混沌时间序列中的仿真结果Table 2.Simulation results of different algorithms in MG chaotic time series.

表3 不同算法在蔡氏电路混沌时间序列中的仿真结果Table 3.Simulation results of different algorithms in chaotic time series based on Chua′s circuit.

5 结论

本文将基于PRQ 采样的Nyström 方法作为稀疏策略应用于核共轭梯度优化法,有效地抑制了核共轭梯度法的核矩阵网络规模增长.进一步,采用半平方法转化柯西核函数生成全局凸的鲁棒函数作为核共轭梯度法的代价函数,提出了一种新的具有鲁棒性的基于PRQ 采样的NCKCG-PRQ 算法.NCKCG-PRQ 在存储需求较低的情况下,与没有采取稀疏策略的CKCG 算法拥有近乎相当的滤波精度.在数值仿真的MG 混沌时间序列和由蔡氏电路真实产生的混沌时间序列的预测中,结果表明在存在脉冲噪声的情况下,NCKCG-PRQ 与其他固定维度的自适应滤波器相比,具有较低计算复杂度和较高的预测精度,有效证实了所提NCKCG-PRQ 算法在混沌时间序列预测中的性能优势.