On JR-rings

HU Xiaomei， Chen Huanyin

(School of Science， Hangzhou Normal University， Hangzhou 310036, China)

On JR-rings

HU Xiaomei， Chen Huanyin

(School of Science， Hangzhou Normal University， Hangzhou 310036, China)

A ringRis called to be a JR-ring if every elementa∈Rcan be written in the form ofa=r+jwhereris a regular element andjbelongs to the Jacobson radicalJ(R). This article gives many properties of JR-rings, and proves thatRis a JR-ring if and only ifR/J(R) is regular and regular elements lift moduleJ(R). A ringRis a Boolean ring if and only if every element inRcan uniquely be represented as the sum of a regular element and an element in Jacobson radical. Further, it investigates the hereditary property of the relevant ring extensions.

regular element; extension ring; JR-ring; Jacobson radical

0 Introduction

A ringRis regular provided that for everya∈Rthere existsb∈Rsuch thata=aba. A ring is called a (S,n)-ring if every element is either a unit or a sum of no more thannunits. Following [1], a ringRis UR-ring if every elementa∈Rcan be written in the form ofa=r+uforris a regular element anduis a unit. These rings are shown to be a unifying generalization of regular rings, clean rings and (S,2)-rings. Following [2], a ringRis a NR-clean ring if every elementa∈Rcan be written in the form ofa=r+bwhereris a regular element andbis a nilpotent. Inspired by these articles and combining the notion of J-clean (a ring is called J-clean if each elementa∈Rcan be written in the form ofa=e+jwhereeis an idempotent andjbelongs to the Jacobson radical), we call an elementa∈Ris JR ifa=r+jwherer∈reg(R) andj∈J(R).Ris called a JR-ring if every element inRis JR.

In this article, we give many properties of JR-rings. We prove thatRis a JR-ring if and only ifR/J(R) is regular and regular elements lift moduleJ(R). A ringRis a Boolean ring if and only if every element inRis uniquely the sum of a regular element and an element inJ(R). Further, we investigate the behavior of these properties under various ring extensions. Throughout this paper, reg(R) denotes the set of all regular elements ofR,J(R) denotes the Jacobson radical ofR,U(R) denotes the set of units ofR.

1 Equivalent Characterizations

Definition1LetRbe a ring. An elementa∈Ris called JR ifa=r+jwherer∈reg(R) andj∈J(R).Ris called a JR-ring if every element inRis JR.

Proposition1EveryJ-clean ring is JR-clean.

ProofThis is obvious.

Proposition2Every JR-ring is a UR-ring.

ProofLeta∈R, chooser∈reg(R) andj∈J(R) such thata+1=r+j,a=r+j-1 wherej-1∈U(R). Henceais UR.

The converse of Proposition 2 need not be true in general.

Example1(3)∩(5)is a JR-ring.

For an one-sided idealIofR, we say that regular elements lift moduloIif whenevera-aba∈Iwitha,b∈R, there exists a regular elementdofRsuch thata-d∈I.

Theorem1LetRbe a ring. Then the following are equivalent:

1)Ris a JR-ring;

2)R/J(R) is regular and regular elements lift moduloJ(R).

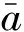
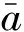
Lemma1LetIbe an ideal ofRwithI⊆J(R). Then idempotents lift moduloIif regular elements lift moduloI.

ProofSee [1, Lemma 2.4].

Corollary1LetRbe an exchange ring. Then the following are equivalent:

1)Ris a JR-ring;

2)R/J(R) is regular.

Proof1)⟹2). That is obvious by Theorem 1.

2)⟹1). SupposeRis an exchange ring, then idempotents can be modulo every left ideal by [3, Corollary 1.3]. Hence every regular element lifts moduloJ(R) by Lemma 1. SoRis a JR-ring.

Theorem2LetRbe a ring. Then the following are equivalent:

1)Ris a Boolean ring;

2) Everya∈Ris uniquely the sum of a regular element and an element inJ(R).

Proof1)⟹2). For everyx∈R,x=x+0. SinceRis Boolean,x2=x. Soxis regular. Clearly, the representation ofxas the sum of a regular element and an element inJ(R) is unique becauseJ(R)=0.

2)⟹1). Leta∈R. Thena+1=r+jis unique, soa=r+j-1 is unique. Clearly,a∈Ris uniquely the sum of a regular element and a unit. HenceRis a Boolean ring by [1, Theorem 3.6].

Proposition3Any homomorphic image of a JR-ring is a JR-ring.

ProofLetφ:R→Sbe a ring epimorphism and supposeRis a JR-ring. Lets∈Sand choosea∈Rsuch thatφ(a)=s. Then we can writea=r+jfor somer∈reg(R) andj∈J(R). Hence,s=φ(a)=φ(r)+φ(j) where clearlyφ(r)∈reg(S) andφ(j)∈J(S). Thus,Sis a JR-ring.

Proposition4LetR=Πα∈IRα. ThenRis a JR-ring if and only ifRαis JR-ring for allα∈I.

Proof(⟹). Suppose thatR=Πα∈IRαis JR. By Proposition 3, it follows that eachRαis a homomorphic image ofR, henceRαis a JR-ring for allα∈I.

(⟸). SupposeRαis JR-ring for eachαand letx=(xi)∈R=Πα∈IRα. Chooseri∈reg(Ri) andji∈J(Ri) such thatxi=ri+ji. Now clearly,r=(ri)∈reg(R) andj=(ji)∈J(R) whichx=r+j. Hence,Ris JR-ring.

Proposition5LetRbe a ring with no non-trivial idempotents. IfRis JR-ring, then it is a (S,2)-ring.

ProofWe firstly verify that reg(R)=U(R)∪{0}. Letr∈reg(R) and writer=ryrfor somey∈R. Sinceryandyrare idempotents inR, then eitherry=yr=1 or at least one ofyrandryis zero. In the first case we getr∈U(R) and the second case implies thatr=0. Now, supposeRis a JR-ring and leta∈R. Writea-1=r+jwherer∈reg(R) andj∈J(R). Ifr=0, thena=j+1 is a unit and ifr∈U(R), thenais a sum of two units. Therefore,Ris a (S,2)-ring.

Proposition6LetRbe a JR-ring and leta∈R. IfaRcontains no nonzero idempotents, thenais the sum of an element in its Jacobson radical and a right unit.

ProofSupposeaRcontains no non zero idempotents. Chooser∈reg(R) andj∈J(R) such thata-1=r+j. Thena=r+(j+1) wherej+1∈U(R) andr=ryrfor somey∈R. Sinceayr=r+(j+1)yr, thena(1-yr)=(j+1)(1-yr). So, (j+1)(1-yr)(j+1)-1∈aR. Since (j+1)(1-yr)(j+1)-1∈Id(R), then by assumption, (j+1)(1-yr)(j+1)-1=0. Hence, 1-yr=0 and thenyr=1. Therefore,ais the sum of an element in its Jacobson radical and a right unit.

Theorem3LetRbe a ring andebe a central idempotent ofR. ThenRis a JR-ring if and only ifeReand (1-e)R(1-e) are JR.

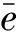
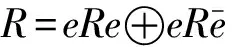
Consider idempotenteinRis central. So

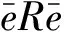
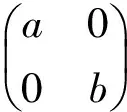
There existy1∈R,y2∈Rsuch thatr1y1r1=r1,r2y2r2=r2. Therefore

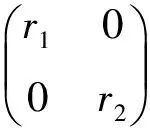
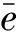
2 Related Rings

Letφbe an endomorphism ofR. We denote the skew power series ring

where addition is naturally defined and multiplication is defined by using the relationxr=φ(r)xfor allr∈R. The power series ringR[[x]] is just the skew power series ring whenφis the identity endomorphism.

Proposition7LetRbe a ring. ThenR[[x,φ]] is a JR-ring if and only ifRis a JR-ring.

ProofSuppose thatR[[x,φ]] is a JR-ring. Then it follows by the isomorphismR≅R[[x]]/(x) and Proposition 3 thatRis JR.

Conversely, suppose thatRis JR-ring. Let

f(x)=a0+a1x+a2x2+…=r0+j0+a1x+a2x2+…

wherer0∈reg(R) andj0∈J(R). Sincer0∈reg(R[[x,φ]]) andj0+a1x+a2x2+…∈J(R[[x,φ]]), soR[[x,φ]] is JR.

Corollary2LetRbe a ring. ThenR[[x]] is a JR-ring if and only ifRis a JR-ring.

Proposition8LetRbe a commutative ring. ThenR[x] is not a JR-ring.

ProofIfxis JR, thenx=r(x)+j(x) for somer(x)∈reg(R[x]) andj(x)∈J(R[x]). By [1, Lemma 4.3],r(x)=eu(x) for somee∈Id(R) andu(x)∈U(R[x]). Now by [4, Lemma 3.5],u(x)=a0+a1x+…+anxn, wherea0∈U(R), anda1,a2,…,an∈N(R),n∈. Setj(x)=b0+b1x+…+bmxm, and we can easy knowb1∈N(R). Thus,

x=e(a0+a1x+…+anxn)+(b0+b1x+…+bmxm).

We have 1=ea1+b1. Henceea1=1-b1∈U(R) and (1-e)ea1=0, 1-e=0. Soa1=ea1∈U(R), a contradiction. ThusR[x] is not a JR-ring.

Theorem4LetRbe a ring. Then the following are equivalent:

1)Ris a JR-ring;

2) The ringTn(R) of alln×nupper triangular matrices overRis a JR-ring.

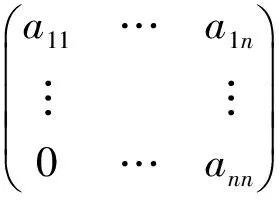
Since there existsyii∈Rsuch thatriiyiirii=rii. Therefore

2)⟹1). SupposeTn(R) is a JR-ring. For anya∈R, diag(a,…,a)∈Tn(R) can be written in the form of

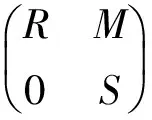
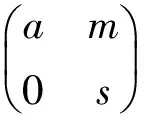
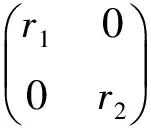
LetRbe a ring and letMbe a (R,R)-bimodule. The trivial extension ofRbyMis the ringR∝M=R⊕Mwith the usual addition and multiplication (r1,m1)(r2,m2)=(r1r2,r1m2+m1r2).

Corollary3For a ringRand a (R,R)-bimoduleM,Ris a JR-ring if and only ifR∝Mis a JR-ring.

Given a groupGand a ringA, the group ringR=AGconsists of all functionsr:G→Awith finite support. The support ofris {g∈G|r(g)≠0}.Ris endowed with ring operation by defining:

0(g)=0.

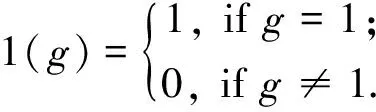
(-r)g=-(r)g.

ThenR(0,1,+,·) forms a ring.

We first consider some cases where a group ring is isomorphic (as a ring) to a direct product of copies of its coefficient ring.

Proposition9LetRbe a ring and let 2 be a unit inR. ThenRis a JR-ring if and only ifRC2is a JR-ring.

ProofLetC2={x|x2=1} and define φ:RC2→R×Rby φ(a+bx)=(a+b,a-b) wherea,b∈R. Thenψis a ring homomorphism. Since 2 is a unit inR, we have thatψis bijective. Therefore,RC2≅R×Rby [5, Proposition 3]. It follows by Proposition 4 thatRis a JR-ring if and only ifRC2≅R×Ris a JR-ring.

Corollary4LetRbe a ring and let 2 be a unit inR. Then for any positive integersk, the following are equivalent:

1)Ris a JR-ring;

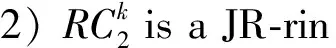
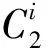
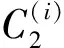
[1] YING Z L, CHEN J L. On UR-rings[J]. J Math Res Expos,2009,29(2):355-361.

[2] KHASHAN H A. NR-clean rings[J]. Vietnam J Math,2016,44(4):749-759.

[3] NICHOLSON W K. Lifting idempotents and exchange rings[J]. Trans Amer Math Soc,1977,229(5):269-278.

[4] XIAO G S, TONG W T. N-clean rings[J]. Algebra Colloq,2006,13(4):599-606.

[5] HAN J, NICHOLSON W K. Extension of clean rings[J]. Comm Algebra,2001,29(6):2589-2595.

关于JR环

胡小美，陈焕艮

(杭州师范大学理学院，浙江 杭州 310036)

一个环R叫做JR 环，如果R中的每一个元素都可以写成a=r+j的形式，其中r是正则元，j属于Jacobson 根.文章给出了JR环的相关性质.证明了R是一个JR环当且仅当R/J(R)是正则元并且正则元关于J(R) 可以提升；R是布尔环当且仅当每个a∈R都可以唯一地表示成一个正则元和Jacobson 根中元之和的形式.并探究了在相关环扩张上的遗传性质.

正则元；环的扩张；JR环；Jacobson根

date：2016-10-07

Supported by the Natural Science Foundation of Zhejiang Province(LY17A010018).

CHEN Huanyin(1963-)，male，Professor，Ph.D.，majored in algebra of basic mathematics.E-mail：huanyinchen@aliyun.com

10.3969/j.issn.1674-232X.2017.06.011

O153.3MSC201016E50;16N20;16S70ArticlecharacterA

1674-232X(2017)06-0628-05