多目标博弈弱Pareto-Nash平衡点集的稳定性研究

李天成，宋奇庆

(桂林理工大学理学院，广西 桂林 541004)

多目标博弈弱Pareto-Nash平衡点集的稳定性研究

李天成，宋奇庆

(桂林理工大学理学院，广西 桂林 541004)

运用一致拓扑的方法研究了支付函数和策略集双重扰动下多目标博弈弱Pareto-Nash平衡点的稳定性，结果表明大多数多目标博弈的弱Pareto-Nash平衡点能够抵抗支付函数和策略集的双重扰动；证明了一定条件下弱Pareto-Nash平衡点的本质稳定连通区的存在性，推导出多目标优化问题弱有效解的本质连通区的存在性，推广了相应文献的结果.

多目标博弈；弱Pareto-Nash平衡点；本质连通区；稳定性

多目标博弈解的稳定性分析是一个重要的研究课题.1956年，Blackwell[1]提出了具有向量值支付函数的零和博弈，Shapley等[2]在1959年引入了多目标博弈平衡点的概念.由于在实际决策中决策者所考虑的目标往往不止一个，而是多个主要目标的综合，因此多目标博弈更符合客观实际，逐渐受到众多学者的关注.

近年来，Yu等[3]在一致拓扑空间上建立了支付函数扰动下广义博弈解集的本质连通区的存在性定理；Yang等[4]通过引入向量值Ky Fan点及其本质连通区的概念，进一步证明了每一个多目标博弈的弱Pareto-Nash平衡点集中至少存在一个本质连通区；Lin[5]讨论了多目标广义博弈在两种不同拓扑空间的弱Pareto-Nash平衡点集的存在性和本质连通区的存在性；余孝军[6]通过定义多目标博弈的加权Nash平衡点集，得出与它对应博弈的弱Pareto-Nash平衡点之间的关系，证明了在一定条件下多目标博弈的弱Pareto-Nash平衡点集的通有稳定性；Song等[7]给出了多目标广义博弈解的通有稳定性结果.

值得指出的是，以上博弈的本质连通区的存在性都是基于支付函数扰动下得到的.2009年，Yang等[8]证明了支付函数和策略集同时扰动下非合作博弈Nash均衡的本质连通区的存在性.这些文献表明在支付函数扰动条件下解的稳定性得到了广泛的研究，而支付和策略集同时扰动下解的稳定性研究还较缺乏.事实上,博弈中保证策略集扰动时解的稳定具有重要意义.基于此,本文将致力于研究支付函数和策略集双重扰动下多目标博弈弱Pareto-Nash平衡点的稳定性.

1 预备知识

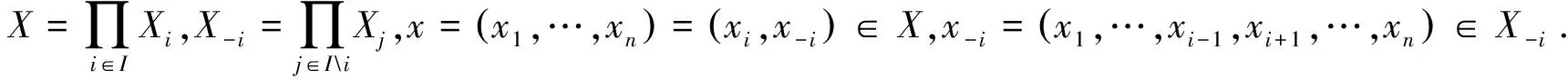
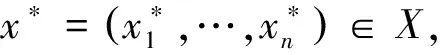
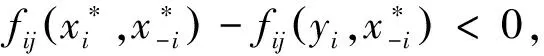
引理1[4]设Γ=(Fi,Xi)i∈I为n人多目标博弈.对∀i∈I,Xi是欧几里得空间Pi中的非空紧凸子集，Fi=(fi1,…,fiki):X→Rki满足

1) 对∀i∈I,j=1,…,ki,fij在X上是连续的；

2) 对∀x-i∈X-i，∀j=1,…,ki,yi→fij(yi,x-i)是凹的，则多目标博弈Γ存在弱Pareto-Nash平衡点.

令M={Γ=(Fi,Ai)i∈I}为多目标博弈Γ的集合，满足：

i)Ai是Xi中的非空紧凸子集；

ii) 对∀i∈I，Fi在X上连续；

iii) ∀i∈I，∀x-i∈X-i以及∀j=1,…,ki，yi→fij(yi,x-i)是凹的.

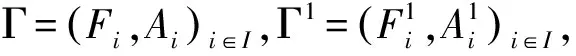
其中h是Hausdorff距离.显然，(M,ρ)是一个完备度量空间.

对∀Γ=(Fi,Xi)i∈I∈M，为了研究支付函数和策略集双重扰动条件下多目标博弈弱Pareto-Nash平衡点集E(Γ)的稳定性，限制策略集Ai的扰动在intXi中，其中intXi表示Xi的相对内部.对于给定的一个博弈Γ，博弈Γ在限制扰动条件下构成的集合为M′，其中

定义2设Γ=(Fi,Xi)i∈I∈M且e(Γ)是E(Γ)的一个闭子集，则称集合e(Γ)为博弈Γ关于M(M′)的本质弱Pareto-Nash平衡点集，如果对任意开集U⊃e(Γ)，存在δ>0，使∀Γ′∈M(M′)，满足ρ(Γ,Γ′)<δ，有E(Γ′)∩U≠∅.称关于M(M′)的本质集m(Γ)为极小本质集，如果m(Γ)为E(Γ)的所有本质集中按包含关系为序的极小元.若本质集e(Γ)是单点集{x0}，则称x0为本质点.

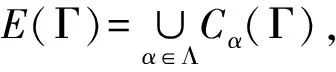
定义3设X和Y是两个度量空间，S:Y→2X是一个集值映射，则有

1) 称S在y∈Y处是上半连续的，如果对任意开集U，有U⊃S(y)，存在y的开邻域O(y)，使对任意y′∈O(y)，都有U⊃S(y′)；如果S在Y上的每一点都是上半连续的，则称S在Y上是上半连续的.

2) 称S在y∈Y处是下半连续的，如果对任意开集U，有S(y)∩U≠∅，存在y的开邻域O(y)，使对任意y′∈O(y)，都有S(y′)∩U≠∅.

3) 如果S在Y上是上半连续的并且对任意y∈Y，S(y)是紧的，则称F是一个上半连续紧映射，记为usco映射.

引理2[9]设M，X是两个Hausdorff拓扑空间，而且X是紧空间.如果集值映射S:M→2X的图Gr(S)是闭的，那么S在M是上半连续的.

引理3[10]设E是度量空间，Y是Baire空间，S:Y→2E是usco映射，则存在Y中的一个稠密剩余集Q，使∀y∈Q，集值映射S在y是下半连续映射.

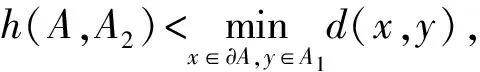
2 支付函数和策略集扰动下多目标博弈弱Pareto-Nash平衡点的本质连通区

定理1集值映射E:M→2X在M上是usco映射.

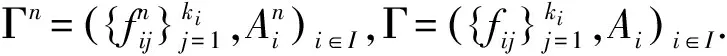
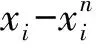
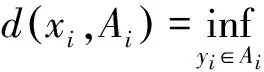
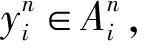
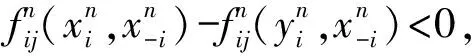
以下采用反证法.假设x∉E(Γ)，则存在yi∈Ai，使

fij(xi,x-i)-fij(yi,x-i)<0,∀j={1,…,ki}.

因fij在X上连续，并且xn→x，故存在正整数N0，使n>N0时有

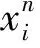
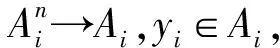
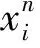
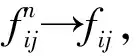
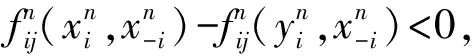
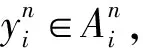
因为X是紧集，并且fij在X上连续，故对∀Γ∈M，E(Γ)都是紧集，所以E是usco映射.

推论1在Baire分类意义下，大部分多目标博弈Γ∈M的每一个弱Pareto-Nash平衡点都是本质解，即存在M的一个稠密剩余集Q，使∀Γ∈Q，博弈Γ是本质的.

证明根据引理3和定理1，存在M的一个稠密剩余集Q，使∀Γ∈Q，集值映射E在Γ上是下半连续的. 对任一Γ∈Q，∀x0∈E(Γ)，取x0的任意开邻域U(x0)，显然E(Γ)∩U(x0)≠φ.因为集值映射E在Γ上是下半连续的，故存在Γ的邻域O(Γ)，使∀Γ′∈O(Γ)，都有E(Γ′)∩U(x0)≠φ.因此，x0是本质解，从而博弈Γ是本质的.

定理2对∀Γ∈M，E(Γ)本身是本质稳定的且至少存在一个极小本质集.

证明i) 任取开集U使U⊃E(Γ).由定理1知集值映射E:M→2X是上半连续的，故Γ存在一个邻域O(Γ)，使∀Γ′∈O(Γ)都有U⊃E(Γ′)，故E(Γ′)∩U≠∅，因此E(Γ)是本质稳定的.

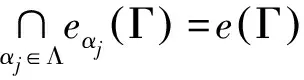
注1定理2表明弱Pareto-Nash平衡点集中存在可以抵抗支付函数扰动和策略集扰动的稳定解集.当局中人的目标为单目标时,多目标博弈转化为单目标的一般的非合作博弈,策略集扰动下的稳定性意味着每一个极小的本质集是完美平衡点.

推论2对∀Γ∈M，如果E(Γ)是单点集{x0}，则x0是本质点，从而博弈Γ是本质的.

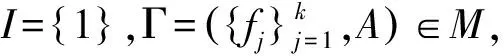
证明显然，多目标博弈Γ的弱Pareto-Nash平衡点集等同于相应多目标优化问题的弱有效解，而根据文献[11]知多目标优化问题的弱有效解集是连通的且由定理2知其是本质的.

定理3对∀Γ∈M，E(Γ)至少存在一个关于M′的极小本质集m(Γ)，并且当每一个关于M′的极小本质集m(Γ)满足m(Γ)⊂intX时,m(Γ)是连通的.

证明i) 显然M′⊂M，使用类似于定理1和定理2的证明方法可知，对∀Γ∈M，E(Γ)至少存在一个关于M′的极小本质集m(Γ).

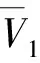
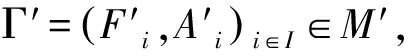
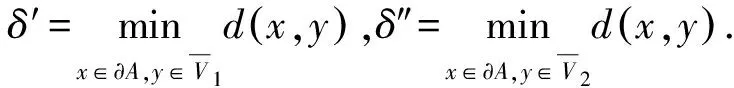
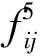
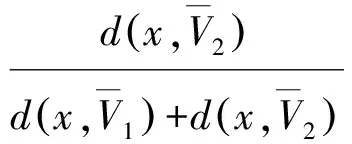
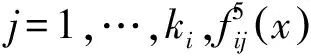
对任意x∈X，有

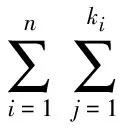
因此，

从而，对∀x∈X，有

所以，

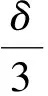
故E(Γ5)∩(V1∪V2)≠∅，即E(Γ5)∩V1≠∅或者E(Γ5)∩V2≠∅.

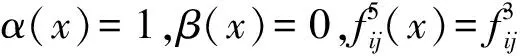
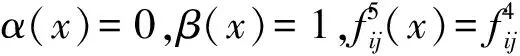
注2对∀Γ∈M，任意极小本质集m(Γ)都可以抵抗支付函数Fi的扰动以及策略集Ai在intXi上的扰动.定理3给出了m(Γ)连通的一个充分的条件m(Γ)∈intX.如果没有限制Ai在intXi的扰动而扩大扰动范围，相应的情况还需进一步的研究.

定理4对于一个博弈Γ∈M，如果m(Γ)∈intX是一个极小本质集，那么E(Γ)至少存在一个本质连通区.

证明根据定理2和定理3，E(Γ)至少存在一个极小本质集m(Γ)且m(Γ)是连通的，故存在α∈Λ，使m(Γ)∈Cα(Γ).对X中的任意开集O，满足O⊃Cα(Γ)，则O⊃m(Γ).因m(Γ)是本质的，故存在δ>0，对∀Γ′∈M，使ρ(Γ,Γ′)<δ，有E(Γ′)∩O≠∅.因此，连通区Cα(Γ)是本质的.

注3定理3和4证明了稳定的平衡点集的连通性,事实上,基于公理化的研究,文[12]表明连通性是稳定Nash平衡点集满足公理的必要条件之一.对任意Γ∈M，如果x0∈E(Γ)且{x0}⊂intX是关于M′的本质连通区，则x0是关于M′的本质弱Pareto-Nash平衡点.

注4当ki=1，∀i=1,2,…,n时，多目标博弈等价于一般非合作博弈，多目标博弈的弱Pareto-Nash均衡对应于通常的非合作博弈的Nash均衡.因此，定理4推广了文[8]中定理3.1相应的结果.

[1] BLACKWELL D. An analog of the minimax theorem for vector payoffs[J]. Pacific Journal of Mathematics,1956,6(1):1-8.

[2] SHAPLEY L S, RIGBY F D. Equilibrium points in games with vector payoffs[J]. Naval Research Logistics，1959,6(1):57-61.

[3] YU J, LUO Q. On essential components of the solution set of generalized games[J]. Journal of Mathematical Analysis and Applications,1999,230(2):303-310.

[4] YANG H, YU J. Essential components of the set of weakly Pareto-Nash equilibrium points[J]. Applied Mathematics Letters,2002,15(5):553-560.

[5] LIN Z. Essential components of the set of weakly Pareto-Nash equilibrium points for multiobjective generalized games in two different topological spaces[J]. Journal of Optimization Theory and Applications,2005,124(2):387-405.

[6] 余孝军.多目标对策的弱Pareto-Nash平衡点集的稳定性研究[J].数学的实践与认识,2008,38(21):227-232.

[7] SONG Q Q, WANG L S. On the stability of the solution for multiobjective generalized games with the payoffs perturbed[J]. Nonlinear Analysis: Theory Methods & Applications,2010,73(8):2680-2685.

[8] YANG H, XIAO X C. Essential components of Nash equilibria for games parametrized by payoffs and strategies[J]. Nonlinear Analysis： Theory Methods & Applications,2009,71(12):e2322-e2326.

[9] KLEIN E, THOMPSON A C. Theory of correspondences[M]. New York: A Wiley-Interscience Publication,1984.

[10] FORT M K. Points of continuity of semi-continuous functions[J]. Publicationes Mathematicae,1951,2:100-102.

[11] WARBURTON A R. Quasiconcave vector maximization: connectedness of the sets of Pareto-optimal and weak Pareto-optimal alternatives[J]. Journal of Optimization Theory and Applications,1983,40(4):537-557.

[12] KOHLBERG E, MERTENS J F. On the strategic stability of equilibria[J]. Econometrica,1986,54(5):1003-1037.

TheStabilityoftheWeaklyPareto-NashEquilibriumPointsSetforMulti-objectiveGames

LI Tiancheng, SONG Qiqing

(College of Science, Guilin University of Technology, Guilin 541004, China)

This article studies the stability of the weakly Pareto-Nash equilibrium points set for multi-objective games under the dual perturbations of payoffs and strategies using uniform topology. The results show that the weakly Pareto-Nash equilibrium point for most multi-objective games has the ability to resist these dual perturbations from payoff functions and strategy sets. Furthermore, the existence of essential connected components of weakly Pareto-Nash equilibrium points is proved under some conditions. And the existence of essential connected components of weak efficient solutions of a multi-objective optimization problem is deduced. These generalize the corresponding results in relevant references.

multi-objective game; weakly Pareto-Nash equilibrium; essential component; stability

2017-02-23

国家自然科学基金项目(11661030)；广西自然科学基金项目(2016GXNSFAA380059).

宋奇庆(1980-)，男，副教授，博士，主要从事博弈论与非线性分析的研究.E-mail:songqiqing@126.com

10.3969/j.issn.1674-232X.2017.06.013

O177.91MSC201091A10；54C60

A

1674-232X(2017)06-0641-06