乘积b-度量空间中扩张型映象的公共不动点定理

刘丽亚，谷 峰

(杭州师范大学理学院，浙江 杭州 310036)

乘积b-度量空间中扩张型映象的公共不动点定理

刘丽亚，谷 峰

(杭州师范大学理学院，浙江 杭州 310036)

在完备的乘积b-空间中，建立一个扩张型条件，研究了公共不动点的存在性和唯一性，从而得到了一个新的公共不动点定理，改进了相关文献的结果.

完备乘积b-空间；扩张型映象；公共不动点

扩张型映象是一类重要的非线性映象,其不动点的存在性备受关注.Czerwik在文[1]中介绍了b-度量空间的概念，文[2-7]在b-度量空间中研究了满足一定压缩条件下非线性算子不动点的存在性问题，得到了一些新结果.

2008年，Bashirov等[8-9]介绍了乘积度量空间的概念.2012年，Florack等[10]研究了在乘积度量空间中的一些实际应用.此后，文[11-14]进一步讨论了乘积度量空间中的不动点问题，得到了相关的公共不动点定理.文[15]利用映象对相容和弱相容的条件，讨论了完备度量空间中4个映象的一类新的压缩映象的公共不动点问题.

受上述文献的启发，本文引入了乘积b-度量空间的定义，在完备乘积b-度量空间中研究扩张型映象的不动点存在性问题，得到了几个新的不动点定理，推广了一些已知的相关结果，而且也是度量空间中某些经典结果在锥度量空间的进一步推广.

1 预备知识

定义1[1]设X是一非空集，令d:X×X→R+满足

(b-1)d(x,y)=0，若x=y；

(b-2)d(x,y)=d(y,x), ∀x,y∈X且x≠y；

(b-3)d(x,y)≤k(d(x,z)+d(z,y)),∀x,y,z∈X,k≥1.

则称函数d是X上的一个b-度量，称(X,d)为b-度量空间，其中k为其系数.

定义2[8]设X是一非空集，令d:X×X→R+满足

(M-1)d(x,y)≥1，∀x,y∈X;

(M-2)d(x,y)=1当且仅当x=y,∀x,y∈X；

(M-3)d(x,y)=d(y,x)，∀x,y∈X；

(M-4)d(x,y)≤d(x,z)·d(z,y),∀x,y,z∈X.

则称函数d是X上的一个乘积度量，称(X,d)为乘积度量空间.

定义3[8]设X是一非空集，令d:X×X→R+满足

(Mb-1)d(x,y)≥1，∀x,y∈X；

(Mb-2)d(x,y)=1当且仅当x=y,∀x,y∈X；

(Mb-3)d(x,y)=d(y,x), ∀x,y∈X；

(Mb-4)d(x,y)≤(d(x,z)·d(z,y))k,∀x,y,z∈X,k≥1.

则称函数d是X上的一个乘积b-度量，称(X,d)为乘积b-度量空间，其中k为其系数.

例1设X是一非空集, (X,d)是一b-度量空间，其中k≥1为其系数.定义d:X×X→R+满足d(x,y)=ed(x,y)，从而可知函数d在X上满足条件(Mb-1)，(Mb-2)和(Mb-3).且易得，对于∀z∈X，有

由此证得(X,d)是一乘积b-度量空间，且k是其系数.

例2定义函数d:(R+)n×(R+)n→R如下：

其中x=(x1,x1,…,xn),y=(y1,y1,…,yn)∈(R+)n,且|·|:R+→R+定义为

其中实数k>1.显然易知d是定义在R+上的乘积b-度量，且k为其系数.

定义4[15]设X是一非空集，(X,d)为乘积b-度量空间.序列{xn}⊂X,n∈+，如果存在x∈X，使得则称序列{xn}收敛于x，也称x为序列{xn}的极限，记为x.

定义5[15]设X是一非空集，(X,d)为乘积b-度量空间.{xn}⊂X，如果对于任意的ε>1，存在+，使得对于任意的m,n≥+，有d(xn,xm)<ε.则称{xn}为(X,d)上的柯西列.

定义6[15]设X是一非空集，(X,d)为乘积b-度量空间.如果对于(X,d)上的每个柯西列在X上都是收敛的，则称(X,d)为完备的乘积b-度量空间.

引理1设X是一非空集，(X,d)为乘积b-度量空间，其中实系数k≥1.序列{xn}和{yn}⊂X分别收敛于x和y∈X，则有

证明由条件(Mb-4)可得

d(xn,yn)≤(d(xn,x)·d(x,yn))k=(d(xn,x))k·(d(x,yn))k≤

(d(xn,x))k·(d(x,y))k2·(d(y,yn))k2.

(1)

d(x,y)≤(d(x,xn)·d(xn,y))k=(d(x,xn))k·(d(xn,y))k≤

(d(x,xn))k·(d(xn,yn))k2·(d(yn,y))k2.

(2)

于式(1)，(2)，令n→∞取极限，又由定义3可得

令{yn}=z，由条件(Mb-4)可得

d(xn,z)≤(d(xn,x)·d(x,z))k.

(3)

d(x,z)≤(d(x,xn)·d(xn,z))k.

(4)

于式(3)，(4)，令n→∞取极限，又由定义3可得

证明由条件(Mb-3)可得

d(yn,t)≤(d(yn,xn)·d(xn,t))k.

(5)

于式(5)，令n→∞取上极限得

定义8[15]乘积b-度量空间(X,d)中的自映象对(f,g)称为是弱相容的，若fx=gx,x∈X,就有fgx=gfx,即d(fx,gx)=1⟹d(fgx,gfx)=1.

例3[8]设X=[0,+∞)，(X,d)是乘积b-度量空间，即d(x,y)=e(x-y)2,∀x,y∈X.f,g是X上的两个自映象，分别定义为

于是可得，当且仅当x=2时，fx=gx=2,进而有fgx=gfx=2.可证得(f,g)是弱相容的.

2 主要结果

定义函数φ:[0,+∞)5→[0,+∞)满足以下条件：

1)φ是非减的，且关于每个元素都连续；

2) 对于∀t≥1，存在函数φ:[0,+∞)→[0,+∞)，使得

φ(t)=min{φ(t,t,t,t,t),φ(t,1,1,t,t),φ(t,1,t,1,t),φ(1,t,1,t,t),φ(t,t,1,t,1)}≥t.

(6)

定理1设X是一非空集，(X,d)是完备的乘积b-度量空间，其中s≥1为其系数.f,g,T,S:X→X为X上的4个自映象，且满足以下条件:

1)fX⊇TX;gX⊇SX;

2) ∃λ∈(0,1),使得∀x,y∈X有

dλ(fx,gy)≥φ{ds4(Sx,Ty),ds4(Sx,fx),ds4(Ty,gy),(d(fx,gy)·d(Sx,gy))s5,(d(fx,gy)·d(Ty,fx))s5}.

(7)

如果f,g,S和T满足下面条件之一，则f,g,S和T有唯一的公共不动点.

(a) (f,S)其中之一连续，(f,S)是相容的，(g,T)是弱相容的；

(b) (g,T)其中之一连续，(g,T)是相容的，(f,S)是弱相容的.

证明任取x0∈X,因为fX⊇TX,所以∃x1∈X,使得fx1=Tx0,又由gX⊇SX,可知∃x2∈X,使得gx2=Sx1,….依此类推可得到序列{yn}⊆X,即为

y2n=Tx2n=fx2n+1;y2n+1=Sx2n+1=gx2n+2,n=0,1,2,….

首先，由条件(Mb-4)可知

d(y2n+1,y2n+2)≤(d(y2n,y2n+1)·d(y2n,y2n+2))s.

(8)

在式(7)中令(x,y)=(x2n+1,x2n+2),又由式(8)可得

即

dλ(y2n,y2n+1)≥φ{ds4(y2n+1,y2n+2),ds4(y2n,y2n+1),ds4(y2n+1,y2n+2),ds4(y2n,y2n+1),ds4(y2n+1,y2n+2)}.

(9)

假设d(y2n+1,y2n+2)>d(y2n,y2n+1)成立，那么d(y2n+1,y2n+2)>1(否则,d(y2n,y2n+1)<1,出现矛盾).由式(6)，可将式(9)整理为

即dλ(y2n,y2n+1)≥ds4(y2n,y2n+1),出现矛盾.所以有d(y2n+1,y2n+2)≤d(y2n,y2n+1).此时由式(6)，(9)可得

即

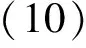
d(y2n+1,y2n+2)≤dh(y2n,y2n+1).

(11)

同理，可证得

d(y2n,y2n+1)≤dh(y2n-1,y2n).

(12)

由式(11)，(12)可得，对于∀n∈,有

d(yn,yn+1)≤dh(yn-1,yn)≤dh2(yn-2,yn-1)≤…≤dhn(y0,y1).

(13)

因此对于∀m,n∈,m>n,根据条件(Mb-4)和式(13)可得

又由y2n=Tx2n=fx2n+1;y2n+1=Sx2n+1=gx2n+2,n=0,1,2,…,可知

(14)

以下证明t是f,g,S和T的公共不动点.

第一步:证明St=t.由式(7)可得

于式(15)，令n→∞,取极限，又由式(6)和引理1，可得

上式即为dλ(St,t)≥d(St,t).又由条件λ∈(0,1)和s≥1,可知d(St,t)=1,即St=t.

第二步:证明gt=Tt=t.由t∈SX⊆gX,所以∃u∈gX,使得gu=St=t.

由式(8)可知

于式(16)，令n→∞,取极限，又由式(6)和引理1，可得

由条件λ∈(0,1)和s≥1,可知d(t,Tu)=1,进而可知Tu=gu=t.又由(g,T)是弱相容的，从而可知gt=gTu=Tgu=Tt.

现证gt=t.在式(7)中令(x,y)=(x2n+1,t),可得

于式(17)，令n→∞,取极限，又由式(6)和引理1，可得

由条件λ∈(0,1)和s≥1,可知d(t,Tgt)=1,进而有gt=t.所以Tt=gt=t.

第三步:证明ft=t.又由式(6)，(7)可知

由条件λ∈(0,1)和s≥1,可得d(t,ft)=0,即ft=t,从而可知ft=gt=St=Tt=t.

于式(18)，令n→∞，取极限，又由式(6)和引理1，可得

由条件λ∈(0,1)和s≥1,可知d(ft,t)=1,进而有ft=t.

接下来证明ft=St成立.在式(7)中，令(x,y)=(t,x2n+2),可得

于式(19)，令n→∞,取极限，又由式(6)和引理1，可得

由条件λ∈(0,1)和s≥1,可知d(St,t)=1,从而有St=t.

重复(I)中的第二步操作，即可得gt=Tt=t.从而可知ft=gt=St=Tt=t.

类似于(I)和(II)的思路，条件(b)也可证得ft=gt=St=Tt=t,即f,g,T和S有公共不动点.

最后证明公共不动点的唯一性.

假设∃t*∈X,使得ft*=gt*=St*=Tt*=t*.那么由式(6)，(7)可得

由条件λ∈(0,1)和s≥1,可知d(t,t*)=1,进而有t=t*.即f,g,T和S的公共不动点具有唯一性.

注1在定理1中如果取S=T=I(I表恒等映像)，即可证得以下结论.

推论1设X是一非空集，(X,d)是完备的乘积b-度量空间，其系数为s≥1.f,g:X→X为X上的两个自映象，且满足以下条件:∃λ∈(0,1),使得∀x,y∈X有

dλ(fx,gy)≥φ{ds4(x,y),ds4(x,fx),ds4(y,gy),(d(fx,gy)·d(x,gy))s5,(d(fx,gy)·d(y,fx))s5}，

则f和g有唯一的公共不动点.

定理2设X是一非空集，(X,d)是完备的乘积b-度量空间，其系数为s≥1.f,g,T,S:X→X为X上的4个自映象，且满足以下条件:

1)fX⊇TX;gX⊇SX;

2) ∃λ∈(0,1),使得∀x,y∈X有

dλ(fx,gy)≥min{ds4(Sx,Ty),ds4(Sx,fx),ds4(Ty,gy),(d(fx,gy)·d(Sx,gy))s5,(d(fx,gy)·d(Ty,fx))s5}.

如果f,g,S和T满足下面条件之一，则f,g,S和T有唯一的公共不动点.

(a) (f,S)其中之一连续，(f,S)是相容的，(g,T)是弱相容的；

(b) (g,T)其中之一连续，(g,T)是相容的，(f,S)是弱相容的.

证明类似于定理1的证明方法，可证得.

推论2设X是一非空集，(X,d)是完备的乘积b-度量空间，其系数为s≥1.f,g,T,S:X→X为X上的4个自映象，且满足以下条件：

1)fX⊇TX;gX⊇SX;

2) ∃λ∈(0,1)，使得∀x,y∈X有

dλ(fx,gy)≥min{ds4(Sx,Ty),ds4(Sx,fx),ds4(Ty,gy)}.

如果f,g,S和T满足下面条件之一，则f,g,S和T有唯一的公共不动点.

(a) (f,S)其中之一连续，(f,S)是相容的，(g,T)是弱相容的；

(b) (g,T)其中之一连续，(g,T)是相容的，(f,S)是弱相容的.

[1] CZERWIK S. Contraction mappings inb-metric spaces[J]. Acta Math Inform Univ Ostrav,1993,1(1):5-11.

[2] AGHAJANI A, ABBAS M, ROSHAN J. Common fixed point of generalized weak contractive mappings in partially orderedb-metric spaces[J]. Math Slovaca,2014,64(4):941-960.

[3] AKKOUCHI M. Common fixed point theorems for two selfmappings of ab-metric space under an implicit relation[J]. Hacettepe Journal of Mathematics and Statics,2011,40(6):805-810.

[4] BOTA M F, KARAPINAR E, MLESNITE O. Ulam-Hyers stability results for fixed point problems via α-ψ-contractive mapping inb-metric space[J]. Abstr Appl Anal,2013,2013:825293.

[5] BOTA M F, KARAPINAR E. A note on “some results on multi-valued weakly Jungck mappings inb-metric space”[J]. Cent Eur J Math,2013,11(9):1711-1712.

[6] AYDI H, BOTA M F, KARAPINAR E, et al. A common fixed point for weakφ-contractions onb-metric spaces[J]. Fixed Point Theory,2012,13(2):337-346.

[7] HUSSAIN N, SHAH M H. KKM mappings in coneb-metric spaces[J]. Comput Math Appl,2011,62(4):1677-1684.

[8] BASHIROV A E, KURPLNARA E M, OZYAPLCL A. Multiplicative calculus and its applications[J]. J Math Anal Appl,2008,337(1):36-48.

[9] BASHIROV A E, MISIRLI E, TANDOGDU Y, et al. On modeling with multiplicative differential equations[J]. Appl Math J Chin Univ,2011,26(4):425-438.

[10] FLORACK L, ASSEN H V. Multiplicative calculus in biomedical image analysis[J]. J Math Imaging Vis,2012,42(1):64-75.

[11] HE X J, SONG M M, CHEN D P. Common fixed points for weak commutative mappings on a multiplicative metric space[J]. Fixed Point Theory Appl,2014,2014:48.

[12] ABBAS M, ALI B, SULEIMAN Y I. Common fixed points of locally contractive mappings in multiplicative metric spaces with application[J]. Int J Math Math Sci,2015,2015:218683.

[13] KANG S M, KUMAR P, KUMAR S, et al. Common fixed points for compatible mappings and its variants in multiplicative metric spaces[J]. Int J Pure Appl Math,2015,102(2):383-406.

[14] ÖZAVSAR M, CEVIKEL A C. Fixed point of multiplicative contraction mappings on multiplicative metric spaces[J]. Mathematics,2012,arXiv:1205.5131v1.

[15] GU F, CHO Y J. Common fixed point results for four maps satisfyingφ-contractive condition in multiplicative metric spaces[J]. Fixed Point Theory Appli,2015,2015(1):165.

ACommonFixedPointTheoremofExpandingMappingsinMultiplicativeb-metricSpaces

LIU liya, GU Feng

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

In complete multiplicativeb-metric spaces, by establishing a new expanding condition, the existence and the uniqueness of the common fixed point are studied, a new common fixed point theorem is obtained, which improves the corresponding results in some references.

complete multiplicativeb-metric space; expanding mappings; common fixed point

2016-08-23

国家自然科学基金项目(11071169)；浙江省自然科学基金项目(Y6110287).

谷 峰(1960-)，男，教授，主要从事非线性泛函分析及应用研究.E-mail：gufeng99@sohu.com

10.3969/j.issn.1674-232X.2017.06.012

O177.91MSC201047H10；54H25

A

1674-232X(2017)06-0634-07