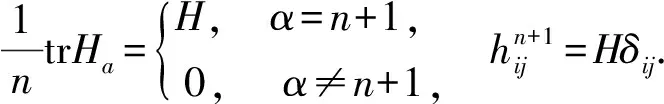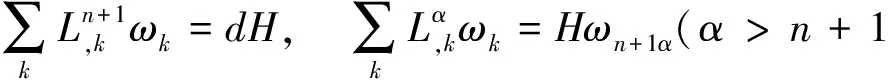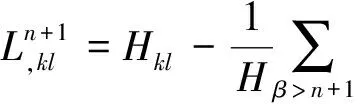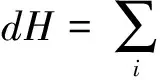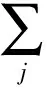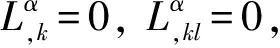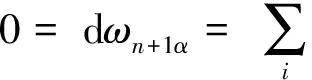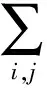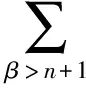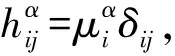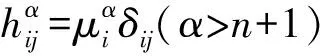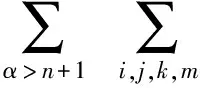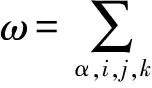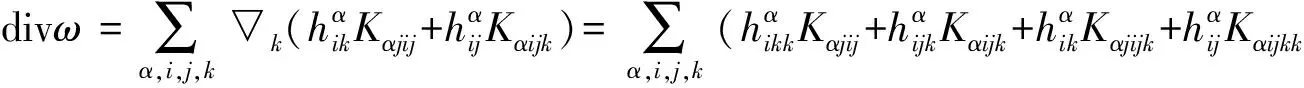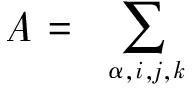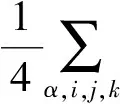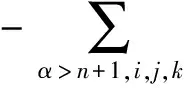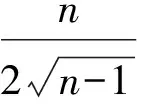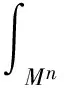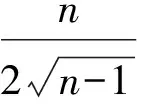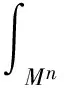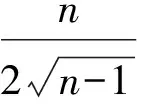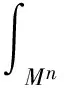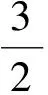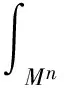拟复射影空间中具有平行平均曲率的全实子流形
刘金梦,宋卫东
(安徽师范大学数学计算机科学学院,安徽 芜湖 241000)
拟复射影空间中具有平行平均曲率的全实子流形
刘金梦,宋卫东
(安徽师范大学数学计算机科学学院,安徽 芜湖 241000)
采用活动标架法研究拟复射影空间CQn+p全实子流形的问题, 并利用自伴算子获得了这类子流形的一些积分不等式.
拟复射影空间;平行平均曲率;积分不等式
0 引言
设CQn+p是具有Kaehler度量的复n+p(实2(n+p))维黎曼复流形,若其曲率张量取为如下形式:
则称CQn+p为拟复射影空间[1].其中:g为CQn+p上的黎曼度量,J为CQn+p的复结构,a,b是CQn+p上的光滑函数,{λA}是CQn+p上的单位向量函数,称λA为CQn+p的生成元.
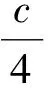
关于具有常数量曲率的子流形,Cheng等已经给出了空间形式的常数量曲率超曲面[2],引入了一个自共轭的二阶椭圆算子.宋卫东等应用这个算子研究了局部对称共形平坦空间中这类子流形的定理[3].对于拟复射影空间近年来也有不少的研究成果[4-6],本文利用自共轭的二阶椭圆算子研究拟复射影空间中具有平行平均曲率向量的全实子流形,得到以下结果.
定理1设Mn是拟复射影空间CQn+p中具有平行单位平均曲率的紧致全实伪脐子流形,适当选取平行平均曲率向量使得CQn+p的生成元沿平行平均曲率向量的分量消失,则有
1) 若p=1,对任意的n,
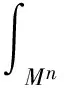
成立;
2) 若p=2,n≥3,则
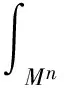
3) 若p≥3,n>7,则
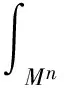
4) 若p≥3,3 文中对各类指标取值范围约定如下: A,B,C,…=1,…,n+p,1*,…,(n+p)*;i,j,k,…=1,…,n; α,β,γ,…=n+1,…,n+p,1*,…,(n+p)*;λ,μ,…=n+1,…,n+p. 设Mn是CQn+p中的实n维全实子流形,J为CQn+p的复结构.在CQn+p上选取局部规范正交标架场 e1,…,en,en+1,…,en+p,e1*=Je1,…,en*=Jen,e(n+1)*=Jen+1,…,e(n+p)*=Jen+p, 使得限制于Mn,{e1,…,en}与Mn相切.以{ωA}表示{eA}的对偶标架场,则CQn+p的结构方程为: 其中, ωij=ωi*j*,ωi*j=ωj*i,ωλμ=ωλ*μ*,ωiμ=ωi*μ*,ωλ*μ=ωμ*λ,ωi*λ=ωλ*i. (1) 将上述形式限制在Mn上,则有 (3) (4) 其中Rijkl,Rαβij分别是Mn的曲率张量R和法曲率张量场关于{eA}的分量.进一步,Mn的平均曲率向量场ξ,平均曲率H,第二基本形式模长平方S可分别表示为 (5) (6) Kαβkj=a(JαkJβj-JαjJβk). (7) 首先计算Mn的第二基本形式分量hij的Laplacian算子△.由式(5),(6)可得 (8) 由式(3),(4),(8)计算得到, (9) (10) 此时,根据定理1的条件可知 λn+1=0. (11) 且 (12) 进一步有 (13) . (14) 其中△是Laplacian算子,在式(14)中取f=H,则 (15) 事实上,根据式(2),(5),(11)能得到 从而□是一个自伴算子[7],故 由于Mn具有平行单位平均曲率向量场,对所有α,有ωn+1α=0,从而由式(12),(13)得 (17) 由式(2),知Kn+1αij=0,对ωn+1α=0外微分, 从而 于是对∀α,Hα,Hn+1可同时对角化,由式(11)知Kn+1kik=Kn+1ijk=0. 由式(9),(10),(15)-(18)经计算有 根据文献[9]知 (19) (20) (21) 又由式(1),(10)及α=n+1知 Jαk=Jαj=0. (22) (23) 由式(5)及引理2可得 (24) 再由式(1),(7),(10)及α>n+1可得Jαk=Ji*k=δik,Jαj=Ji*j=δij,故有 (25) (26) 引理3[2]设Mn是(n+p)维黎曼流形Nn+p中的任一子流形,则 (27) 从而 A≥-n(n-1)b2-divω≥-pn(n-1)b2-pdivω. (28) 再利用Kn+1jij=Kn+1ijk=0和式(28),故 由式(24)-(29)及引理3得 因为Mn具有平行单位平均曲率向量,所以H为常数,根据式(17),(19),(23),(30)得 成立. [1] 宋卫东,朱岩.拟复射影空间中的全实伪脐子流形[J].吉林大学学报(理学版),2012,50(4):673-677. [2] CHENG S Y, YAU S T. Hypersurfaces with constant scalar curvature[J]. Math Ann,1997,225(3):195-204. [3] 宋卫东,刘敏.关于局部对称共形平坦空间中具有常数量曲率的子流形[J].数学物理学报,2010,30(4):1102-1110. [4] 朱岩,宋卫东.拟复射影空间CQn+p中的全实极小子流形[J].吉林大学学报(理学版),2013,51(5):855-859. [5] 吴丹,宋卫东.拟复射影空间CQn+p中的全实伪脐2-调和子流形[J].宁夏大学学报(自然科学版),2014,35(2):117-119. [6] 何俊秀,孙宝磊,姚纯青.拟复射影空间CQn+p中的全实伪脐子流形[J].西南师范大学学报(自然科学版),2016,41(2):30-35. [7] 华义平,宋卫东.局部对称黎曼流形中某类超曲面的刚性定理[J].吉林大学学报(理学版),2009,47(6):1125-1130. [8] ZHANG J F. A rigidity theorem for submanifolds inSn+pwith constant scalar curvature[J]. Journal of Zhejiang University Science,2005,6(4):322-328. [9] 刘敏,宋卫东.复射影空间中具有常数量曲率的全实子流形[J].纯粹数学与应用数学,2012,28(6):749-757. TotallyRealSubmanifoldswithParallelMeanCurvatureinaQuasi-complexProjectiveSpace LIU Jinmeng, SONG Weidong (College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China) In this paper, the totally real submanifoldsCQn+pin a quasi-complex projective space is studied by the method of moving frames, and some integral inequalities are obtained by using a self-adjoint operator. quasi-complex projective space; parallel mean curvature; integral inequality 2017-02-28 国家自然科学基金项目(11371032);安徽省自然科学基金项目(1608085MA03). 宋卫东 (1958—),男,教授,主要从事微分几何研究.E-mail:swd56@sina.com 10.3969/j.issn.1674-232X.2017.06.014 O186.12MSC201053C42 A 1674-232X(2017)06-0647-06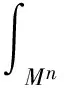
1 预备知识

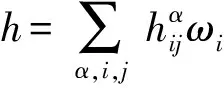

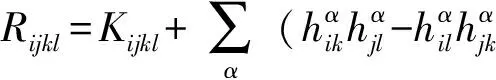
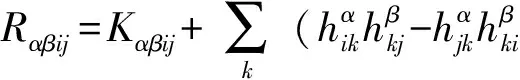


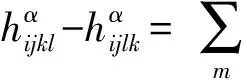
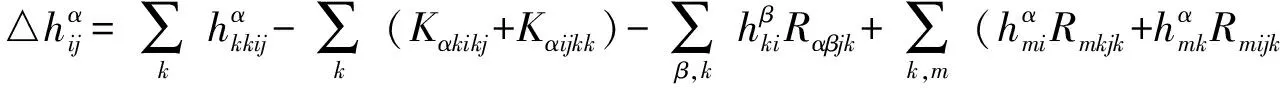
2 定理的证明