作图是几何教育的根基*——兼论清末民国时期几何作图教科书的发展

代 钦

(内蒙古师范大学科学技术史研究院 010022)

几何作图一直以来在几何教育中扮演着重要角色.自古希腊泰勒斯在几何中引进证明思想、毕达哥拉斯学派发现无理数以及欧几里得编写《几何原本》等数学事件，牢固地确立了几何学崇高地位并形成了近2000年的传统，这种传统并没有因笛卡儿创立解析几何而被终止.进入19世纪以后欧几里得《几何原本》的教育功能被质疑，遭到挑战.中国1904年确立新的数学教育体制，其后各发展阶段的“课程标准”中提出了几何作图的教学目标和要求，并翻译、编写出版了一系列中小学几何作图教科书，直至1949年中华人民共和国成立，几何作图教学受到重视.

1 对几何作图及几何教育沿革的初步认识

1.1 几何作图的认识

图是一种语言，是人类互相交流的重要工具之一.人离开了图无法交流，甚至可以说人离开了图就回到原始状态.图有各种各样，丰富多彩.我们可以将这些图分类为图像、图象和图形三大类型.自然界的事物或建筑物的描摹形成图像；抽象数学表达式或方程的直观表达可以形成图象，一般叫做函数图象；空间中的各种要素之间关系的抽象描绘可以形成几何图形.在自然界和人类生活中，图无处不在.数学、地理学、动植物学、物理化学、人文科学等主学科都借助图表述自己的内涵.事实上，人类和抽象符号的创造的原始形态也是从图开始的.无论是图的何种形态，它们都是表达人类情感思想的一种方式.图的学习和认识与其他语言一样，是人类生活中不可或缺的重要组成部分.因此，自古以来无论是东方还是西方都格外重视图的教育，特别表现在几何学、艺术等领域中.图的学习不仅是为了掌握交流或表达思想感情，而且也是为了养成人的严谨的思维和良好的工作习惯.在教育的各个不同阶段，图的教育扮演着极其重要的角色.在图像和图形的学习过程中，图形的学习具有基础性地位，图形的学习就是作图的学习，简单讲就是几何作图的学习.在学校数学教育中，使学生牢固掌握作图的基本知识、方法和技能以及作图工具的功能等方面皆为作图教学的基础性工作.图有以下功能：其一是图将具体事物进行抽象化，将复杂的事物进行简单化，表示个别事物的普遍意义.其二是将抽象的思想事物进行形象化、直观化，帮助人们易于把握抽象思想.图在从具体到抽象、从抽象到具体之间起到桥梁作用，正如古希腊哲学家柏拉图所说那样，数学是“把灵魂拖着离开变化世界进入实在世界的学问.”[注]柏拉图.理想国[M].郭斌和，张竹明，译.北京：商务印书馆，1995:521.其三，作图过程也许点燃创造的火花，激起灵感，引出问题，从而推动数学的健康发展.古希腊的“几何作图不能问题”的提出就是一个明证.

1.2 几何教育沿革的认识

古希腊泰勒斯在几何学中引进证明思想给数学注入了新鲜血液和理性精神，接着毕达哥拉斯学派发现无理数引起数学的第一次危机以及欧几里得编撰《几何原本》以后，几何学的神圣地位被确立，直至笛卡儿创立解析几何之前被尊为不可挑战的传统.解析几何创立后，几何学的传统地位有所减弱，但是它与代数学喜结良缘，并驾齐驱，实现了数学的内部和谐，在其后的发展中作为教科书的《几何原本》内容体系没有改变.18世纪中叶之前《几何原本》和亚里士多德学说被西方社会尊崇为金科玉律，不得违背，否则受到相应处罚.然而，17世纪中叶开始，法国等国家的数学教育悄然地开始了.拉米(Bernard Lamy)所著教科书《Les èlèments de gèomètrie,ou de la mesuredu corps》(1684)已经打破了欧几里得《几何原本》体系，而且一直被使用到18世纪中叶，影响颇大，如法国伟大思想家卢梭在1737年—1740年间的回忆中高度评价该书：“我又开始学习初级几何，但是，由于我想弥补我记忆力差的缺点，所以老是翻来覆去地无数次从头学起，因而进展不大.我不喜欢欧几里得的几何学，因为它侧重于一连串题目的演示，而不阐述概念的联系.我特别喜欢拉米神甫的几何学.这位神甫是我最喜欢的著述家之一，直到现在，我还依然饶有兴趣地读他的书.接着，我又开始研究代数，我还是用拉米神甫的代数学作我的入门读物.”[注][法]卢梭.卢梭全集第1卷忏悔录(上)[M].李平沤，译.北京：商务印书馆，2013:316-317.1741年，法国数学教育家亚历西斯克罗德克雷洛在其所著教科书序言中对欧几里得几何学提出了批评：“两圆相交，自然不能同心，一三角形包一三角形，自然内形三边之和，小于外形三边之和，尽人皆知，毋庸赘述，而欧几里得氏，乃不惮烦而证明之，宁非异事.固执之诡辩家，尝否认普通自然之理，几何家理应出而辩服之…，但至今日，事变时迁，非复往日之面目，凡关于心地明白，一见即能了解之辩论，在今日为徒费光阴，仅足混淆真理而招读者之厌弃之事.”[注]卡约黎.初等算学史[M].曹丹文，译.上海：商务印书馆，1931：231.到了19世纪以后，西方国家出现提倡数学教育的实用性的现象，这也表明了人们对纯粹的几何学教科书《几何原本》的怀疑.1836年英国著名心理学家和哲学家哈密尔顿(W.Hamilton，1788—1856)、1844年德国的著名哲学家叔本华(Schopenhauer，1788—1860)等学者对数学教育的“形式陶冶说”(注：“形式陶冶说”即为“数学是锻炼思维的体操”之概括说法)提出了质疑.叔本华提出[注][德]叔本华.作为意志和表象的世界[M].石冲白，译.北京：商务印书馆，1995:115—119.：

欧几里德所证明的一切如此如彼，都是人们为矛盾律所迫不得不承认的，但是何以如此如彼，那就无法得知了.所以人们几乎是好像看过魔术表演一样，有一种不太舒服的感受；事实上，欧几里德大多数的证明都显著地像魔术.

通常在几何学中，例如在毕达哥拉斯定理中，需要作出一些直线，却不明白为什么要这样做；往后才发现这些原来都是圈套，出其不意地收紧这圈套的口，就俘虏了学习人的信服，学习人只得拜倒而承认一些他完全不懂个中情况的东西.事实竟至于此，学习人可以从头至尾研读欧几里得的著作，然而仍不能对空间关系的规律有任何真正的理解；代之而有的只是背诵一些来自此等规律的结果.这种原属经验的，非科学的知识就如一个医生，他虽知道什么病要用什么药，却不认识两者间的关系一样.

图1 毕达哥拉斯定理的特例

毕达哥拉斯定理也告诉了我们直角三角形的一种隐秘属性.(如图1)欧几里得那矫揉造作，挖空心思的证明，一到“何以如此”就避而不见面了；而下列简单的，已经熟知的图形，一眼看去，就比他那个证明强得多.这图形让我们有透入这事的理解，使我们从内心坚定地理解[上述]那种必然性，理解[上述]那种属性对于直角的依赖性；在勾股两边不相等的时候，要解决问题当然也可以从直观理解入手.

1869年，博物学家赫胥黎在《两周评论报》上发表文章贬低数学说：“算学一科，全不知观察、实验、归纳、因果等法.”1869年在另外一种杂志《Macmillan》上又发表言论道：“算学之训练，几纯属演绎方法.算学家之起手，仅需少数之公理，一见即能了解，无待证明者，其余工作，即由此等公理演绎而出.”[注]卡约黎.初等算学史[M].曹丹文，译.上海：商务印书馆，1931：254.

F.克莱因对上述言论进行了严厉的反驳.1901年，杜威、桑代克(Thorndike)等著名学者重新提倡数学教育的新的“形式陶冶说”[注]佐佐木元太郎.现代数学教育史年表[M].东京：圣文社，1985：87..杜威和桑代对数学学习心理学以及数学功能，杜威著作有《数的心理学及其在算术教学法上的应用》，桑代克著作有《算术心理学》和《代数心理学》，均没有中译本.

数学界虽然不同意一些著名哲学家、科学家对数学的藐视，但是他们也意识到学校数学内容确实存在问题.因此，首当其冲的是英国应用数学家培利选择了摆脱欧氏几何束缚，开创实验几何的道路.这对后来的世界教育产生了深刻影响.欧美出现了各种实验几何教科书、几何作图教科书、用器画教科书或几何画教科书.

虽然出现中学几何学内容削减、引进实验几何，弱化推理几何的现象，但是自古希腊以来对几何作图的规范性要求并没有减弱.古希腊伟大的哲学家和教育家苏格拉底和某一数学家关于“整体是否等于其部分”的谈话，充分展示了几何作图规范性要求的重要性，也反映了几何学习不能仅凭直观经验和拥有社会地位者的傲慢态度.故事如下：有一天苏格拉底与一位几何学家谈论“全体大于部分”这个几何学公理，他设计了这样一个题目，使几何学家大吃一惊[注]吴国盛.科学的历程(上册)[M].长沙：湖南科学技术出版社，1995:105.：

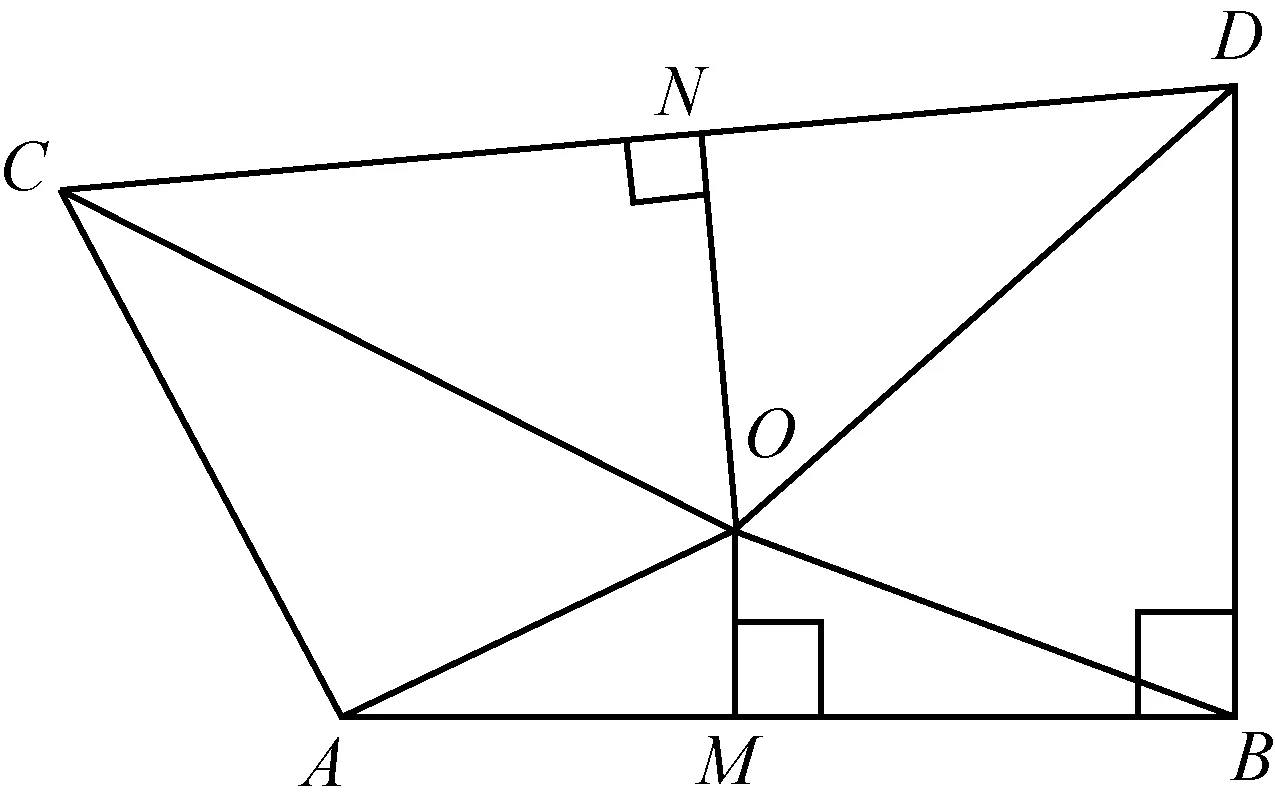
图2

如图2，自线段AB的两端作等长的线段AC和BD，使∠ABD为直角，∠BAC为钝角.连接CD并作线段AB、CD的中垂线OM、ON，相交于O点.则AO=BO，CO=DO，(中垂线上任一点和两端点等距离).又AC=BD.

所以△AOC≌△BOD(SSS)，

所以∠OAC=∠OBD(对应角) ，

又∠OAB=∠OBA(等腰三角形底角)，所以∠BAC=∠ABD.即钝角等于直角.

这说明，作为几何学家的对话者过于相信自己的直觉和经验，熟练地制作了几何图形，意外地出现了谬误的结果.这也告诉人们即使是几何学家或老练的数学教师也不能一点含糊，作图时要遵循几何作图的规范性要求.

又如，欧几里得回答托勒密国王提问那样：“几何学中没有为国王专门铺设的道路.”

2 清末民国时期几何作图教学要求及其特点

几何作图并不是西方世界独有的教育现象，它在古代的不同数学文明中均有不同形式的存在，如在中国最迟在数学经典著作《周髀算经》中就有很多几何作图.但中国古代数学中的几何作图却没有提出明确的要求和程序性说明，这种现象也对研究中国古代几何学带来了诸多不便.而西方数学格外重视几何作图的规范性要求，这也是数学的严谨性体系所不可或缺的内在要求.在下面介绍的《20世纪中国中小学课程标准·教学大纲汇编(数学卷)》[注]课程教材研究所.20世纪中国中小学课程标准·教学大纲汇编(数学卷)[Z].北京：人民教育出版社，2001.清末民国时期几何作图教学要求皆为从西方国家传进来的舶来品.

2.1 清末民国时期几何作图教学要求

清末民国时期数学教育制度沿革情况：1904年《奏定中学堂章程》；1923年《新学制课程标准纲要》；1929年《初级中学算学暂行课程标准》；1929年《高级中学普通科算学暂行课程标准》；1932年《初级中学算学课程标准》；1932年《高级中学算学课程标准》；1936年《初级中学算学课程标准》；1936年《高级中学算学课程标准》；1941年《修正初级中学数学课程标准》；1941年《修正高级中学数学课程标准》；1941年《六年制中学数学课程标准草案》；1948年《修订初级中学数学课程标准》；1948年《修订高级中学数学课程标准》.自1904年至1922年，中国中学不分初中和高中，小学分初等小学和高等小学，高等小学相当于后来的初中.自1922年“新学制”的“六三三制”颁布实施后才出现初中和高中，学制分别三年，小学为六年制.

自1904年至1922年，几何作图教学要求简明扼要，基本延续了1904年《奏定中学堂章程》提出的要求：“其讲几何，须详于理论，使得应用于测量求积等法.”1922年以后对初中和高中几何作图教学都提出了“教材大纲”要求和“实施方法”要求，直至1949年除微调以外没有大的变化.初中又分为“实验几何”和“理论几何”作图要求.下面以1941年的“标准”中几何作图要求为例说明，1941年分别制定了《修正初级中学数学课程标准》、《修正高级中学数学课程标准》和《六年制中学数学课程标准草案》，其中的几何作图要求如下：

初中教材大纲：实验几何——平面几何图形；基本作图题；理论几何——基本作图法；几何——作图之方法.

初中实施方法概要之教法要点：(1)先从实验几何引起学生兴趣，输入基本概念；(2)使学生知定理及作图解决问题；(3)养成作图精确、写式整洁、立论有本诸习惯；(4)轨迹与作图仅授大意.

高中教材大纲：第一学年：作图——(甲)基本作图与基本作图题；(乙)作图法——轨迹交截法、代数分析法、变形法及变位法.

高中实施方法概要之教法要点：(1)使学生对于几何基础、定理证明法、求轨迹法及作图法有透彻之了解；(2)注重轨迹及作图，发展学生探讨之能力.

六年制中学教材大纲：(第三学年)实验及平面：平面几何图形之认识，基本图形之作法；(第四学年)平面之续：基本作图法及作图题之证明(关于直线形及圆)；(第五学年)几何(平面之续及立体)：作图题法——轨迹交截法，代数分析法，变形法及变位法.

六年制中学实施方法概要之教法要点：

(1)几何教学之开始，迟代数两学期，其教材之排列，与代数平行，亦亘七学期之久，每学期亦各有其主要教材：第一学期为实验几何之部，自第二学期起始讲授推理几何，由是而直线形、圆、比例、面积、轨迹、作图，以进于立体之部，关于近世几何之简单定理，亦略涉及.

(2)几何事项，本为直观教材，故应从实验几何入手，俾易引起学生兴趣，而基本观念即藉以灌输.实验几何教学时，应使学生自动作图、度量，尤以立体图形，更应自作纸板，或其他模型，以确实其观念.无论平面或立体，凡关于度量之简单公式，应利用实验方法验明之.

(3)轨迹作图应特加注意，因此二者不独可用以推理证题，尚可发展学生探求发明之能力.

(4)几何证题及作图，应就可能范围内，尽量采用代数方法，求已知条件与未知条件间之关系.

(5)立体几何以空间性质及量法为主，务使学生能透视平面上之图形，了解各种立体之构造，宜与用器画取得联络.

由此可见，通过几何作图，使学生牢固掌握几何知识的同时，培养学生学习几何之兴趣、良好的学习习惯和探究问题之能力.

2.2 清末民国时期几何作图教学要求的特点

几何作图内容和要求呈现以下特点

(1)自1904年至1922年之间，“章程”和“课标”中的几何教学内容和作图要求基本没有变化.

(2)1922年颁布“新学制”后中学分为初中和高中，学制分别为三年.初高中都设置平面几何内容，由于民国时期施行教科书多元化制度的原因，有时候初中和高中的平面几何的有些内容重复出现.初高中有“教材大纲”和“实施方法”两项，在前者中说明具体教学内容，在后者中提出具体的实施方法.

(3)在初中几何中设置“实验几何”和“理论几何”(亦称“推理几何”)，在两者中均提出了“切实训练基本图形画法，务使整洁正确.”之几何作图要求，“实验几何”侧重于以培养学生学习兴趣和动手能力为目的，以具体直观材料为教材，以实验法或作图法为手段证明几何命题或解决几何问题.例如，同高同底的柱体和椎体的体积关系、不在同一条直线上的三个点确定一个圆(如何作三角形的外接圆)、如何将一个圆弧复原为一个圆等问题的解决都是通过作图方法.另外，初中的实验几何和理论几何的内容并不是截然分开的，有一定的交叉或者重复.初中几何特别强调在作图过程中使学生得出几何图形的基本性质.

(4)高中注重作图法的讨论，将作图法渗透于轨迹问题和几何证明问题中，同时强调在作图题中应用代数方法(即为数形结合方法).高中还要求适当添加几何画和透视法的补充教材.高中几何作图教学也应该与中学图画科的用器有机结合，以便在相关学科之间融会贯通.

3 几何作图教科书

3.1 几何作图教科书出版概况

在清末数学教科书建设方面，小学数学教科书由国人自编的较多，中学数学教科书绝大多数为翻译或编译日本、欧美的教科书.随着社会的进步，中国中学数学教科书由最初的翻译、编译外国教科书，最终实现了自主创新，使数学教科书具有了自己的特色.就一般而言，清末中学数学教科书呈现“新颖性”特点、“多元性”特点、“滞后性”特点和“合作性”特点.几何作图教科书也呈现这些特点.1912年，中华民国成立后，教科书发展进入一个新的阶段，体现新政体的指导思想.中学数学教科书主要以自编为主，以翻译为辅，有条件的中学使用自编教科书和外文教科书.民国时期，编纂中学数学教科书的学者愈来愈多，可谓形成了教科书建设者群体.几何作图教科书的发展虽然没有和算术、代数、几何和三角学教科书的发展那样壮观，但在这个历史时期也有不可小觑的重要地位.从表1可见其发展概貌.

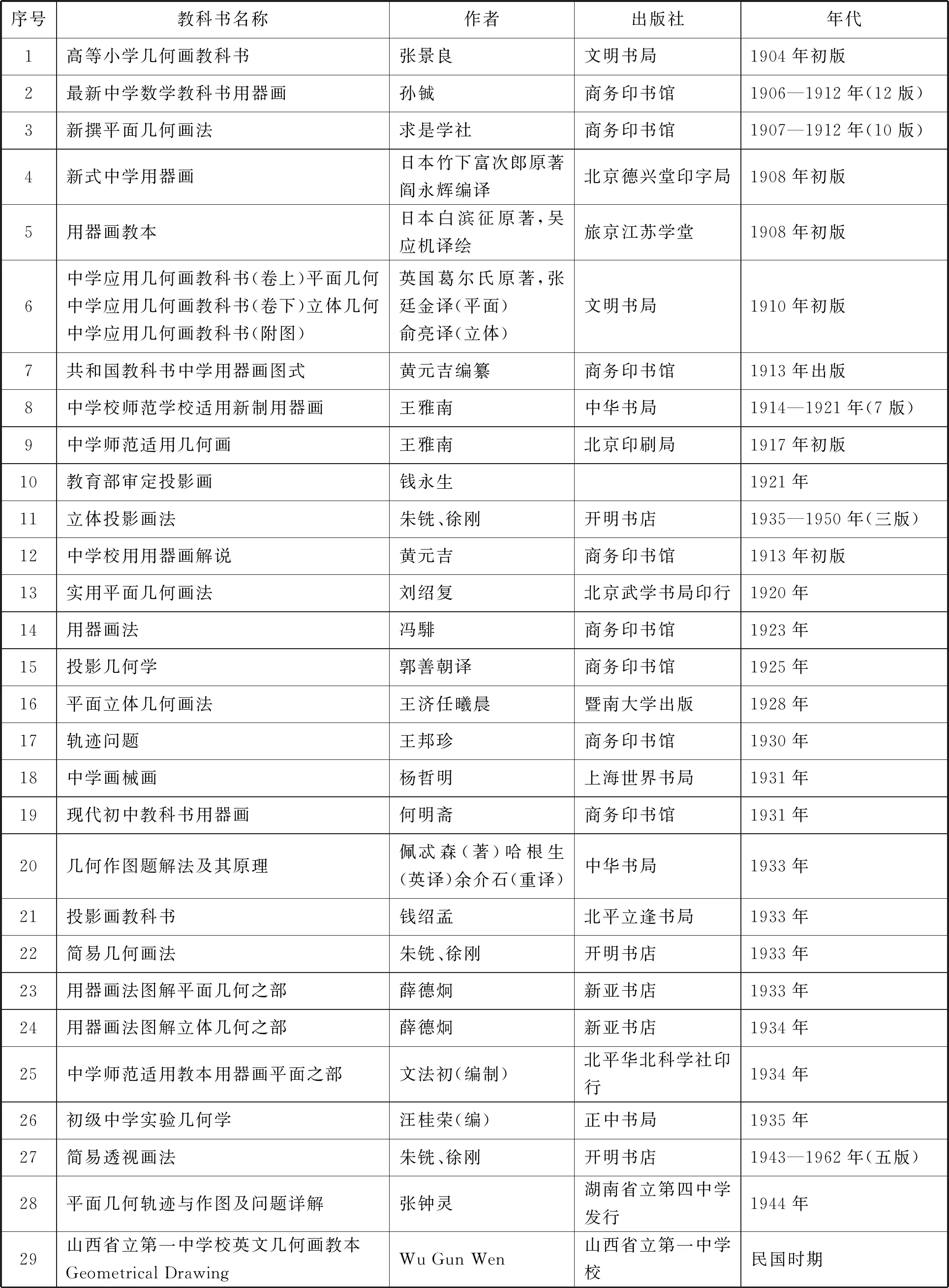
表1 清末民国时期几何作图教科书(部分)

3.2 几何作图教科书个案

(1)“学堂章程”颁布后的最早的几何作图教科书

图3 教科书封面和序

张景良编的《高等小学几何画教科书》(文明书局，1904年，119页)目录如下：

1.释名；2.绘图器具；3.图板及丁字尺；4.绘图纸及定针；5.三角板及曲线板；6.尺度及分度线；7.规；8.铅笔橡皮；9.钢笔及虚线笔；10.小刀及涂料；11.颜料及着色笔；12.盛色具及水杯；13.修理器械法；14.绘图者之心得；15.使用器械法；16.绘关于直线之图法；17.绘关于角之图法；18.绘关于圆之图法；19.绘关于三角形之图法；20.绘关于四角形及多角形之图法(附：圆周求分为数等分法)；21.绘关于面积之图法；22.绘关于容切之图法；23.绘关于抛物线之图法；24.绘关于椭圆之图法；25.绘关于双曲线之图法；26.制缩尺之法；27.缩尺之制度；28.绘示力图法；29.绘机械图法；30.绘金属及木材之剖面图法；31.绘测量图法；32.测量图记号；33.文字方位及轮廓；34.着墨之法；35.施彩色之法；36.颜料之调和法；37.测量图之彩色；38.建筑图及机械图之彩色；39.绘图之次序；40.写图及缩图法(附：绘地球图之经纬线法).

(2)“最新中学教科书”中作图教科书

《最新中学教科书用器画教科书》目录——平面几何画法(92页)

总说；第一编—直线：直线、角、直线形；第二编—圆：切线、内容形、外切形、弧成椭圆、卵形、平螺旋线；第三编—比例：线之比及比例、相似性、缩图、放大图；第四编—面积：分积、等积；第五编—曲线：椭圆、抛物线、双曲线、平螺旋线.

《最新中学教科书用器画教科书》目录——投影画法(58页)

总说；第一编—平面：点、直线、直线形、圆形；第二编—立体：立体之切断及其解展、柱体、椎体；第三编—相贯体：柱体椎体球体等之相贯体.

图4 最新中学教科书用器画

(3)中学应用几何画教科书(上下、附图三册，文明书局，1910年)

图5 中学应用几何画教科书

(卷上)目录 第一编 平面几何(174页)

第一章 总论；第二章 角与线；第三章 角度及直线之量法；第四章 三角形；第五章 四边形；第六章 多角形；第七章 圆；第八章 比与比例；第九章 尺度；第十章 相似性；第十一章 作图法；第十二章 直线形之内切级外接；第十三章 圆之内切形；第十四章 圆之外切形(外接形)；第十五章 内切圆；第十六章 外接圆；第十七章 椭圆之简易画法；第十八章 面积；第十九章 杂题；第二十章 用几何画作种种花纹法.

(下卷)目录 第二编 立体几何(134页)

第一章 总论；第二章 释名；第三章 关于立体之射影画法；第四章 关于立体剖面之画法；第五章 杂题.

第三编 画法几何

第一章 释名；第二章 点之射影；第三章 直线之射影；第四章 平面；第五章 杂题.

第四编 图解演算法

第一章 定单位法；第二章 加法及减法；第三章 乘法及除法；第四章 乘方；第五章 平方根.

由上述三种教科书目录可见，首先，小学几何画教科书中有除基本工具及其用法之外，在没有学习相关理论知识的情况下安排了椭圆、抛物线、双曲线、圆周的等分、不同图形的容切、剖面图、地球的经纬线的画法等内容.这种现象犹如先学习语言再学习语法那样，先学习作图，到中学后再学习其理论知识.其次，三种教科书的平面部分内容除表述上有所不同外，其内容基本相同.立体部分的内容主要有射影或投影几何和画法几何之简单内容.再次，三种教科书都注重了几何画的知识技能在生活实际上的应用.最后，清末的几何作图教科书的内容体系一直延续到民国终结，但是进入民国后射影几何画和画法几何各自单独形成教科书，不在立体几何画中.

(4)几何作图教科书作图举例

清末几何作图教科书中的基本作图内容一直延续到民国结束，但有些表述有所不同.如清末教科书中将西方的ABCD……等改写为甲乙丙丁……，如图6.图7为正多边形作图方法，图8为椭圆的作图方法.关于具体作图方法，另写论文讨论.

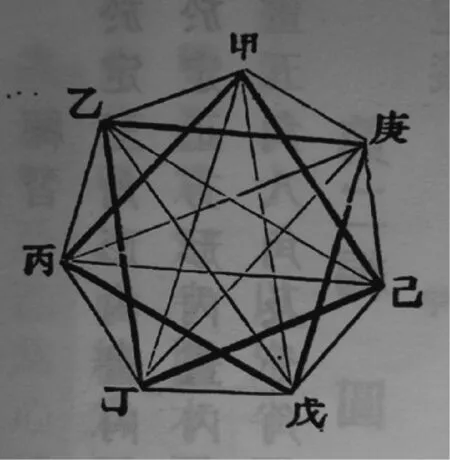
图6 清末教科书中几何作图

图7 民国教科书中的几何作图

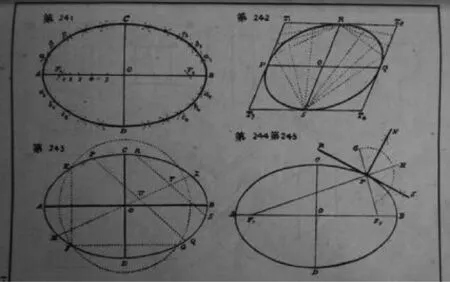
图8 民国教科书中的几何作图

3.3 几何作图教科书特点

1.各种几何作图教科书没有统一的名称，出现“用器画”、“几何画”和“几何作图”等名称.“用器画”和“几何画”等术语最早出现在日本明治时期几何教科书中，也没有得到统一，因此，我国数学教育工作者在以日本为师的大背景下直接使用了这两个术语.

2.几何作图内容不只局限在几何作图教科书中，而且在平面几何、立体几何和解析几何教科书中以不同形式不同水平出现.

3.将作图教科书内容分为三个类型，第一类型为基本作图知识，包括作图工具的认识、角平分线、垂直平分线等基本图形的作图方法；第二类型为常用的经典图形的制作，如正五边形、正六边形、正七边形等；第三种类型为日常生活中常见的几何图案;第四种类型为几何问题解决作图题.

4.几何作图教科书被审定的占少数，多数为没有经过审定.从使用或版次来看，1904年至1912年间清末的几何作图教科书种类和版次较多，相对而言民国作图教科书的使用和版次有所减少.从整体上看，几何作图教科书的发展在出版企业、翻译或编译渠道、内容体系、作者群等方面均呈现多元化特征.

5.由“表1：清末民国时期几何作图教科书(部分)”可知，个别地区或个别学校自行编写几何作图教科书，个别学校使用外文几何作图教科书，这些现象也反映了几何作图教学被重视的情况.

4 结语

教育和教学是一种创造性的工作，它从最基本的知识和技能的学习开始.几何作图的基础知识的学习、基本技能的掌握以及用作图方法解决问题，不仅仅是单纯的作图技能的学习，而是在这些过程中学生也能够学到几何学的思想方法.教育是一种循序渐进的过程，不能急于求成，更不能采取极端化的做法.因此，即便是信息技术高度发达的今天，不能把几何作图的工作全部交给几何画板，而应该让学生自己脚踏实地地学习几何作图，亲身体验作图的过程和乐趣，使他们能够找到学习几何的感觉.数学教师，他们的一言一行都感染着学生，影响着学生.现在存在的问题是数学教师重视几何作图不够，更尤甚者少数数学教师自己也没有养成良好的作图习惯，有些数学教师在作图时根本不适用作图工具，很“熟练”地作图以显示自己的“熟能生巧”之水平.这些现象也会潜移默化地影响他们的学生和学生的学生，如此下去的后果是不堪设想的，这还需要论证吗？！

致谢：衷心感谢博士生张彩云同学提供珍贵文献——《中学应用几何画教科书》(三册，1910年).