再谈“好的例题教学是照亮学生解题的灯塔”

陈延付

(浙江省景宁中学 323500)

当我阅读数学通报2017年第56卷第4期时，深深地被臧华老师的《好的例题教学是照亮学生解题的灯塔》(下文简称：文[1])这个标题所吸引，但阅读之后总感觉不尽入味，怎样的例题教学才是好的例题教学？好的例题教学学生需要有怎样的知识、经验、能力等的储备？师生在例题教学过程中怎样自然地进行数学思维的交流、数学语言的交流、数学探索精神的交流？本文将对“好的例题教学”再作一些探讨，交流看法，期望能引起读者共同深入的讨论这一个话题.

例已知函数f(x)=x3-ax2(a∈R).若f(x)的切线过点(0,1)，且过点(0,1)的切线有2条，求实数a的值.[1]

1 审准题，说想法

(1)审题“准”，抓关键，抓题眼，揭示已知条件和所求结论的关系.

关键点：过点(0,1)的切线，切点未知(巡视课堂，学生有误，个别纠错).

题眼点：切线有2条(几何条件).

精准点：求实数a的值(代数方程).

(2)说想法，学生说自然想法，师生讨论、整理、归纳解题的想法.

想法1(代数想法)

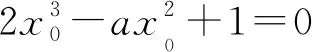
想法2(几何想法)

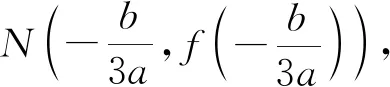
根据三次函数图像分析过点(0,1)的切线有2条,可借助多媒体课件(几何画板动画)演示，探求数形结合的解题想法.

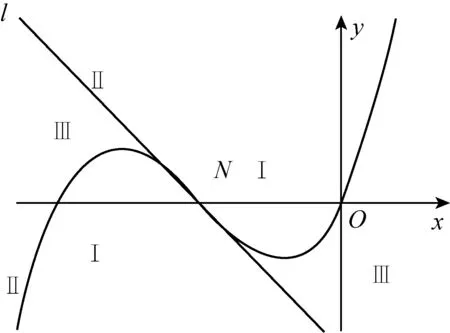
图1

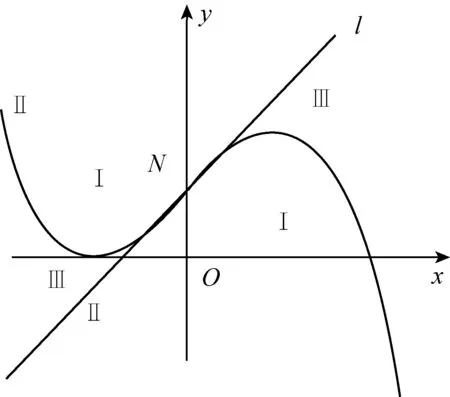
图2

2 明思路，定解法

通过师生讨论，教师点拨初步形成了解决问题的想法，明确了解题的思路方向，对解题的可行性进行试算、评估、选择，设计算理、算法，确定解题的方法.

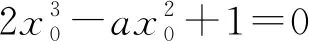
2.1 代数解法

文[1]提供了方案1，方案2处理求解：

方案1: 构造函数g(x)=2x3-ax2+1，研究函数的零点个数问题(含参讨论，运算量大).

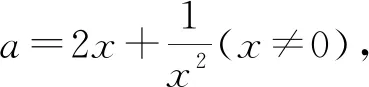
方案4: 方程2x3-ax2+1=0有二重等实数根x0,令g(x)=2x3-ax2+1，

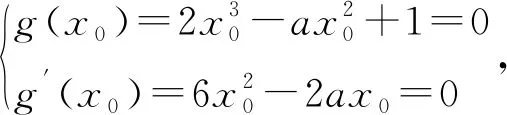
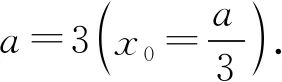
2.2 几何解法

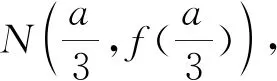
确定解法，板书(或展示)师生讨论的最佳解题方法(一般方法或通性通法).

解：设切点坐标为(x0,y0),

则切线方程为：y-y0=f′(x0)(x-x0)，

由过点(0,1)的切线有2条，

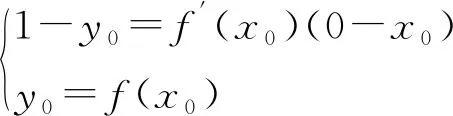
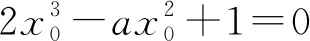
即是方程 2x3-ax2+1=0有两个不等实数根，

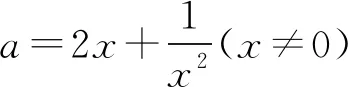
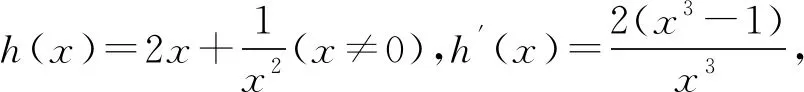
h(x)在区间(-∞,0)及(1,+∞)单调递增,在区间(0,1)递减，

当且仅当a=h(1)=3时，

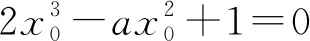
即过点(0,1)的切线有2条，则a=3.

3 研变式，深探究

变式1:文[1]过点(0,1)的函数f(x)=x3-ax2(a∈R)切线有3条(或1条)，求实数a的取值范围.(方案3或几何法方案5求解较好，a>3(a<3))

变式2：过点(0,b)的函数f(x)=x3-ax2(a∈R)切线有2条，求实数a与b的关系.

(方案2、3、4或几何法方案5求解较好，求得结论为，a3=27b)

变式3：(1)若直线y=x与曲线y=x3-3x2+ax相切，则实数a=.(2)若直线y=x与曲线y=x3-3x2+ax-1相切，则实数a=.

变式4：已知函数f(x)=ax+cosx-sinx的图像上存在两条互相垂直的切线，则实数a的取值范围是

变式5：(1)若关于x的不等式k(x-1)≤x(1+lnx)恒成立，则k的取值范围是.

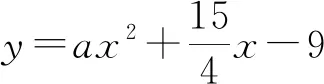
经过问题变式研究，问题深入探究，教师讲在学生困惑处，学生理解了其中蕴含的数学解题自然想法；理清了问题解题思路.

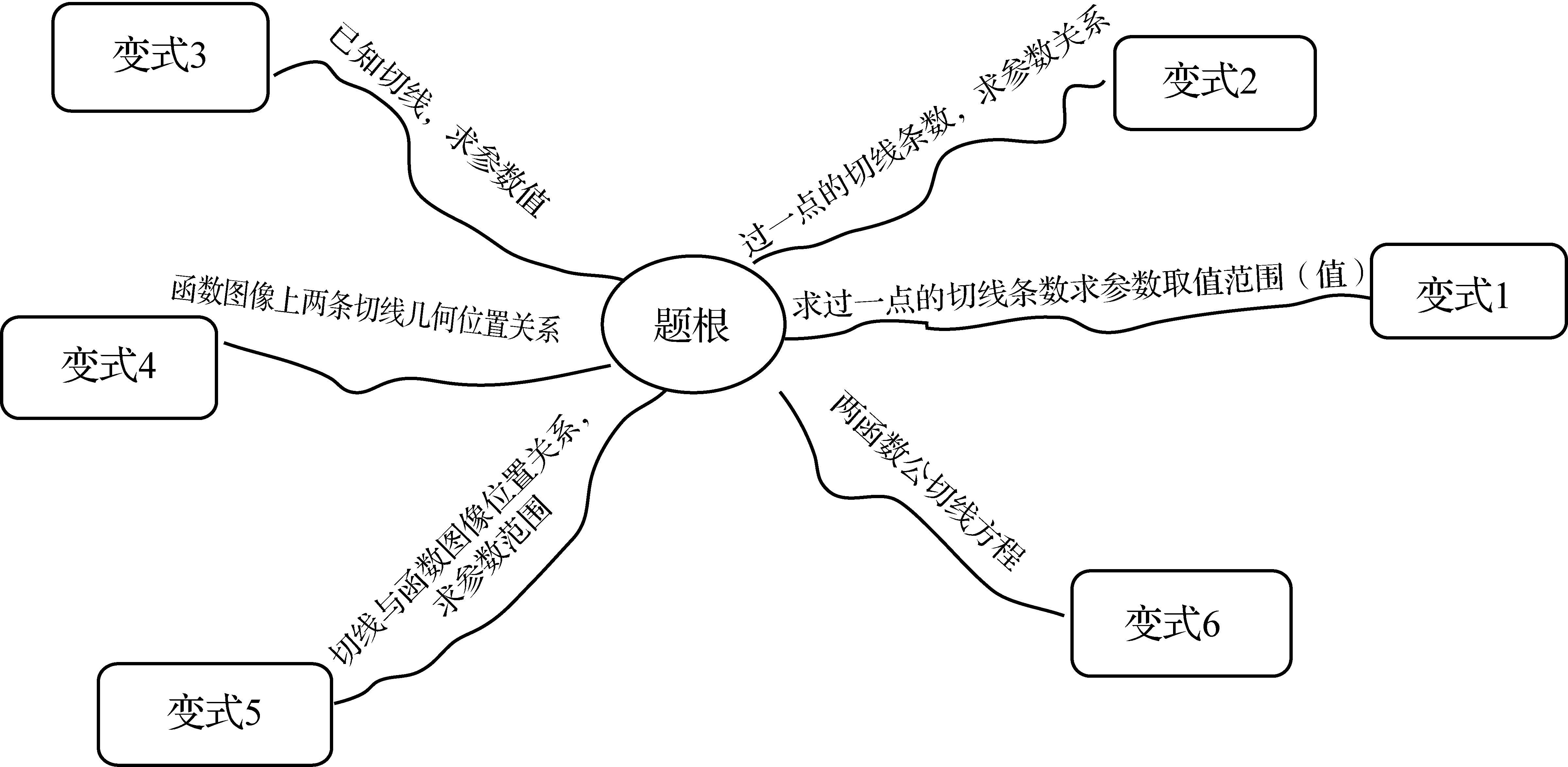
4 寻题根，促反思

通过寻找题根，问题类型归纳整理分析，深刻的反思问题，学生进一步清楚了所求问题的本质.从切线的概念(方程)到导数的几何意义，从代数想法到代数解法，从几何想法到几何解法，从解题运算方案试算、选择、优化到问题解法的一般化(通法)……

题根：已知点P(1,3)是曲线C:f(x)=ax3+x+1(a∈R)上的一点,求曲线C在点P处的切线方程.

师生经历了“审准题，说想法”、“明思路，定解法”、“研变式 ，深探究”，“寻题根，促反思”，这样的例题教学让学生“会一题，通一类”，促进学生对数学问题本质的理解能力进一步提升，促进学生数学探索精神的进一步提升，促进学生数学素养的进一步提升.