直面问题 展现思路 积累经验——基于“数学基本活动经验”下的问题解决讲评

黄 云

(广东省深圳市第二实验学校 518000)

1 问题的提出

数学基本活动经验的积累是提高学生数学素养的重要标志.帮助学生通过运用数学的思维和语言进行阅读、运算、推理和表达的实践活动来积累数学基本活动经验，是数学教学的重要任务.笔者认为，针对学生解题中出现的典型问题，设计由学生谈过程、说困惑，师生共同找错因、给评判的讲评课，让学生阐述自己在解题中的真实思维过程，反思、辨析出现困惑或发生错误的原因，不仅可以有效地纠正错误，避免同类错误的再次发生，而且可以帮助学生积累数学基本活动经验.本文以一堂高三检测讲评课为例给予说明，敬请读者批评指正.

2 讲评的设计

课前由学科代表组织学生筛选汇总典型问题，根据解题过程中出现的相同困惑、错因进行分组，并选出各组发言人.每个问题解决的讲评由三个环节组成：

环节1：谈过程说困惑，由各组发言人分别阐述在解答本题过程中出现的困惑；

环节2：找错因作评判，由学生及教师共同找出错因并予以评判；

环节3：理思路积经验，由教师或学生给予解题思路上的剖析或点拨.

3 课堂教学概述

3.1 问题呈现

学科代表根据课前要求，汇总了若干出错率高的典型问题.本文仅选以下3个问题为例，进行讲评概述.

问题1已知直线m:y=kx+1与双曲线c:x2-y2=1的左支交于A,B两点，直线l过点P(-2,0)和线段AB的中点M，求l在y轴上的截距b的取值范围.

问题2已知数列{an}满足：a1=2，an+an-1=4n-2(n≥2).

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)若数列{bn}满足：b1+3b2+7b3+…+(2n-1)bn=an+5，求数列{bn}的通项公式.

问题3设函数f(x)=ax2+(2b+1)x-a-2，a,b∈R.若a≠0，函数y=f(x)在[3,4]上至少存在一个零点，求a2+b2的最小值.

3.2 讲评环节

环节1：谈过程说困惑,由各组发言人分别阐述在解答本题过程中出现的困惑(由于谈及的困惑较多，限于篇幅，本文仅选9个予以呈现).

发言人1：问题1存在如下困惑.

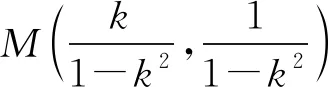
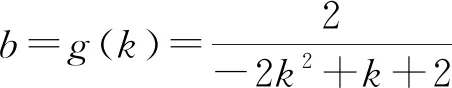
发言人2：汇总问题2有如下困惑.

困惑4：对于an-an-1=f(n)(n≥2)型问题，用累加法直接可求解，但对于an+an-1=f(n)型问题，不知如何入手，只好放弃.

困惑5：由an+an-1=4n-2得an+1+an=4n+2，两式相减得an+1-an-1=4，发现数列{an}的奇数项和偶数项分别是公差为4的等差数列，但后续不知如何求解下去？

困惑6：顺利求解了(Ⅰ)，但在求解(Ⅱ)时，对于如何利用条件b1+3b2+7b3+…+(2n-1)bn=2n+5来求bn，似曾相识却又想不起来，没有找到相应的转化方法.采用“归—猜—证”法，没有找到规律，也没能求出{bn}的通项公式.

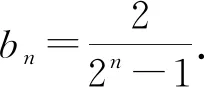
发言人3：问题3有如下困惑.

困惑8：通过阅读，理解“至少存在一个t∈[3,4]，使得at2+(2b+1)t-a-2=0成立”，也即：关于t的方程at2+(2b+1)t-a-2=0(a≠0) 在[3,4]上至少有一个实数根，令f(t)=at2+(2b+1)t-a-2(a≠0)，接下来对a>0和a<0分别讨论有一根或两根的情况，来确定a,b的范围，再求a2+b2的最小值.由于含有两个参数a,b，讨论难度较大，无法进行下去，就此搁浅.

环节2：找错因作评判,由学生及教师共同找出错因并予以评判.

教师：请问,对方程(1-k2)x2-2kx-2=0求根或是讨论根的情况，能否求得直线l的方程？如果得不到直线l的方程，能求得l在y轴上的截距b的取值范围吗？

学生1：不能，必须先想办法求出直线l的方程.容易看出困惑1中的前两种想法都属于没有读懂和理解题意，弄错了求解方向，偏离了求解目标，将“求l在y轴上的截距b的取值范围”淹没在了对方程根的探讨上；第三种思路虽然求得了截距b，但由于二次函数值域的求解方法遗忘，解题受阻，即便没有遗忘二次函数值域的求法，如果没有求出k的范围，也只能获得错误答案.如困惑2.

教师：困惑1中的前两种思路，只停留于问题的表象，而没有抓住问题的本质！在解题中，困惑的产生可能有多方面的因素：如知识缺漏、数学语言理解的偏差、推理运算的错误、方法选择不当等等.要避免这些现象的出现，不仅要学会用数学的语言和思维去破解题意，更要清楚在求解方程和函数问题时需要抓住的关键点是什么？

学生3回答：在求解方程问题时，不可忽视方程根的范围；在求解函数问题时，一定要优先考虑函数的定义域，两者之间要实施等价转化.

学生5：困惑6属于急促情境下的思维断片或是分类讨论经验缺失而导致的；困惑7由b1+3b2+7b3+…+(2n-1)bn=2n+5与b1+3b2+7b3+…+(2n-1-1)bn-1=2n+3两式作差求bn，运算最为快捷，但由于没注意n≥2，导致了运算错误.这种错误在数列问题的求解中会时常出现，必须引起注意！

教师：温馨提示,数列问题中，一旦出现n-1的下标(项数)，必须考虑n≥2为前提.

学生6：困惑8由至少存在一个t∈[3,4]，使得at2+(2b+1)t-a-2=0成立，也即关于t的方程at2+(2b+1)t-a-2=0(a≠0) 在[3,4]上至少有一个实数根，数学语言转化做得好，但对a>0和a<0讨论方程根时，思维受阻，困于其中.

环节3：理思路积经验，由教师或学生给予解题思路上的剖析或点拨.

3.2.1 丰富感性经验，提升理性经验

对于函数与方程问题，如问题1，学生由于感性经验不足和理性经验的缺乏，往往仅会单一考虑运用函数知识或是运用方程知识来解决问题.不能透过问题的现象扣住问题的本质，将函数与方程(不等式)有机地联系起来综合考虑问题.有时即便想到了函数与方程的结合，也不能简洁、完整的实施两者的等价转化，特别是方程的根与函数定义域之间的等价转化.在解题中，需要强化阅读、发现和理解问题的能力，来丰富函数与方程问题的感性经验；强化运算、推理和表达问题的能力，来提升函数与方程问题的理性经验，以期获取快捷流畅的解题思路.学生对问题1提供了多种解题思路，现仅选学生7所呈现的求解思路：

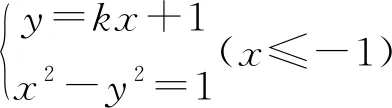
3.2.2 注重直接经验，兼顾间接经验

直接经验和间接经验都是学生获取知识或解决问题的重要途径.数学学习的过程就是不断积累经验的过程，问题解决，实际上就是利用已有的间接或直接经验去获取或体验新的直接经验的过程.间接经验是学生数学学习中不可或缺的经验，在对问题实施转换与化归的数学活动中，有时固有的间接经验可能会阻碍直接经验的获取.例如，在面对如问题2这种新情境时，学生更需注重直接经验的获取，兼顾间接经验的运用，学会用“数学的方式”获取新的直接经验，并能利用直接经验去优化解题过程，灵活解决问题.在问题2的多种求解思路中，仅选了三位学生的解题思路呈现如下.

学生8：问题2(Ⅰ)大致有三种思路：

其一,直接对an+an-1=4n-2进行配凑得:(an-2n)+[an-1-2(n-1)]=0，发现{an-2n}是公比为-1的等比数列，进而求得an=2n；

其二,由题设条件得到an+1-an-1=4后，对n分奇偶讨论求得an=2n；

其三,采用“归纳—猜想—证明”的方法，求得an=2n.

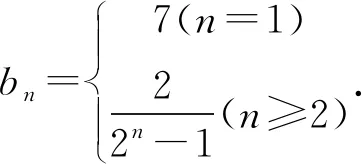
学生10：问题2(Ⅱ)采用“归纳—猜想—证明”的方法求{bn}的通项公式，排除b1=7后，从b2开始找规律，同样也很快可以获得正确的答案.

教师：问题2(Ⅰ)的转化点是an+an-1=4n-2，可以通过配凑法、奇偶讨论法、“归—猜—证”法来实施转化；问题2(Ⅱ)的转化点是b1+3b2+7b3+...+(2n-1)bn=an+5，可以通过构建作差或“归—猜—证”实施转化. 在转化过程中要谨防缺漏！如果出现n-1，必须考虑n≥2！解题中既要注重间接经验的运用，更要注重直接经验的获取.

3.2.3 积累活动经验,激发创新思维

“经验”是指从多次实践中所体现的解决问题的“综合能力”.数学基本活动经验应指学生在数学活动中所体现的解决问题的“综合能力”. 只有让学生参与到活动中来，在不断的“会做数学”的过程中，才能使这种经验得到积累和提升.教学中应注意引导学生通过阅读、运算和画思维导图等显性化活动，分析问题的本质进而明确转化的方向；对于复杂问题，如问题3，则要引导学生利用数学概念的多元联系表示，将问题转化为简单的、直观的表示方式，从而创造性地建构从已知到未知的桥梁并最终实现问题的解决.下面呈现了学生11、12、13对问题3转化和求解的过程：

图1

教师：很好，利用数形结合实现了“以形助数”! 在问题解决的过程中，首先要学会善用数学概念的多元联系去明确目标，知道求解什么？其次，就是要善于建构过程明晰的思维导图来实现从已知向目标的转化.面对复杂问题，更要善用已有的经验，创造性地建立已知与未知的联系，并从中提炼、积累新经验.

教师：解决问题3的关键是如何利用同构关系实现将|OP|转化为t函数！以上3名同学融入了自己对问题的理解和感悟，用“数学的方式”富有创意地解决了问题.

4 体会与感悟

基于不同类型学生数学实际水平，开展“直面问题 展现思路，积累经验”的教学活动，用数学的育人方式“对学生进行数学思维和语言的教育，即通过数学的阅读、运算、推理和表达的训练，使学生正确理解数学知识，形成用数学知识合理解释直至创造性地解决问题的能力”，让不同层次的学生获得不同程度的收获与体验.笔者认为，日常教学中重视数学基本活动经验的积累和数学思想方法的渗透，对提升学生数学核心素养是极为有益的.