中考数学(北京卷)2015-2017年评价改革综述与思考

王亮亮

(北京教育考试院 100083)

1 改革背景

以《国家中长期教育改革和发展规划纲要(2010-2020年)》、《义务教育数学课程标准(2011年版)》的颁布为标志，新一轮数学课程改革开始.2014年3-4月，教育部印发了《完善中华优秀传统文化教育指导纲要》和《全面深化课程改革落实立德树人根本任务的意见》，9月份国务院颁布了《国务院关于深化考试招生制度改革的实施意见》.2016年9月，教育部发布了《教育部关于进一步推进高中阶段学校考试招生制度改革的指导意见》…….这些文件的发布，让这一轮课程改革更具整体性，推进更加协同，实施更加系统.

当前，数学新课改已进行五年，对课程改革的讨论已有很多，其中考试改革与教学改革的关系是一个重要方面.本文意在从考试改革如何助力教学改革的角度，梳理改革思路，总结实践经验，思考考试改革给教学改革带来的影响.

2 改革基础

准确把握《义务教育数学课程标准(2011年版)》实质性的变化是改革实施的必要前提.

2.1 “双基”是一切的基础

2011版课标指出：“知识技能”既是学生发展的基础性目标，又是落实“数学思考”“问题解决”“情感态度”目标的载体；以知识和技能为载体，引导学生感悟其中的数学思想，积累数学活动经验.这说明数学“双基”是学生数学学习的基础；是数学应用的基础；是学生后继学习的基础；是创新人才培养的基础；是一个人终身学习的基础.

2.2 注重数学知识的系统性

实验稿课标指出：“以传授系统数学知识”为基本目标的“学科体系为本”的数学课程结构让位于“以促进学生发展”为基本目标的“学生发展为本”的数学课程结构.实验稿课标不再首先强调是否向学生提供了系统的数学知识.但2011版课标指出：教师对数学基础知识的教学，不但要注重知识，还要注重知识的“生长点”和“延伸点”，注重知识间的逻辑联系，使学生会把局部数学知识置于整体知识体系中，引导学生加强对数学的整体把握和宏观认识.

2.3 在过程中感悟数学思想和积累数学活动经验是数学思维形成的必要前提

2011版课标指出：数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在最高层次上的抽象与概括……；数学活动经验需要在“做”的过程和“思考”的过程中积淀，是数学学习活动过程中逐步积累的.这说明要使学生真正理解数学知识，理解数学的精髓，感悟数学的理性精神，就需要使学生在学习过程中不断感悟数学思想和积累数学活动经验，将建立的数学感悟、数学的直观上升到理性的思考，这都是数学思维形成的必要前提.

2.4 核心概念既是课程与教学目标的核心，又彰显了数学能力

2011版课标提出：建立数感、符号意识和空间观念，形成几何直观和运算能力；发展数据分析观念，感受随机现象；发展合情推理和演绎推理能力；增强应用意识，提高实践能力；体验解决问题方法多样性，发展创新意识.这几乎覆盖了所有的核心概念，而这些核心概念又体现了抽象概括能力、推理能力、发现和提出问题等贯穿于整个数学课程的数学能力.

2.5 注重内容结果与学习过程并重的评价

2011版课标在“评价建议”中强调要注重学生学习过程的评价.学习评价的目的是全面了解学生数学学习的过程和结果，促进学生形成自我反思，进行自我激励，实现全面发展.过程性评价又与学生认知知识形成过程、整体把握数学知识、感悟数学思想、积累数学活动经验、发展数学思维等方面相辅相成、密不可分.

3 改革思路

2015年，初步提出了“内容结果与学习过程”并重的评价体系，确立了“注重基础，能力立意”的评价原则.对于基础知识的考查不再是单一的，而是以基础知识为载体，通过对学习过程的考查，将评价体系的落实落脚于对数学能力的考查，实现对学生全面的评价.

经过2015-2016年实践，完善、明确了两方面考查要求.第一，“四基”要求.基础知识明确注重知识的整体性和知识之间内在联系的考查；基本技能明确考查技能操作步骤中蕴含的原理；基本思想明确对知识本质及规律理性认识的考查；基本活动经验明确活动过程中必须积累的经验，尤其是思维经验.第二，能力要求.明确指出对于能力的考查要以思维考查为核心，包括对数学知识、数学知识形成与发展过程、数学知识灵活应用.

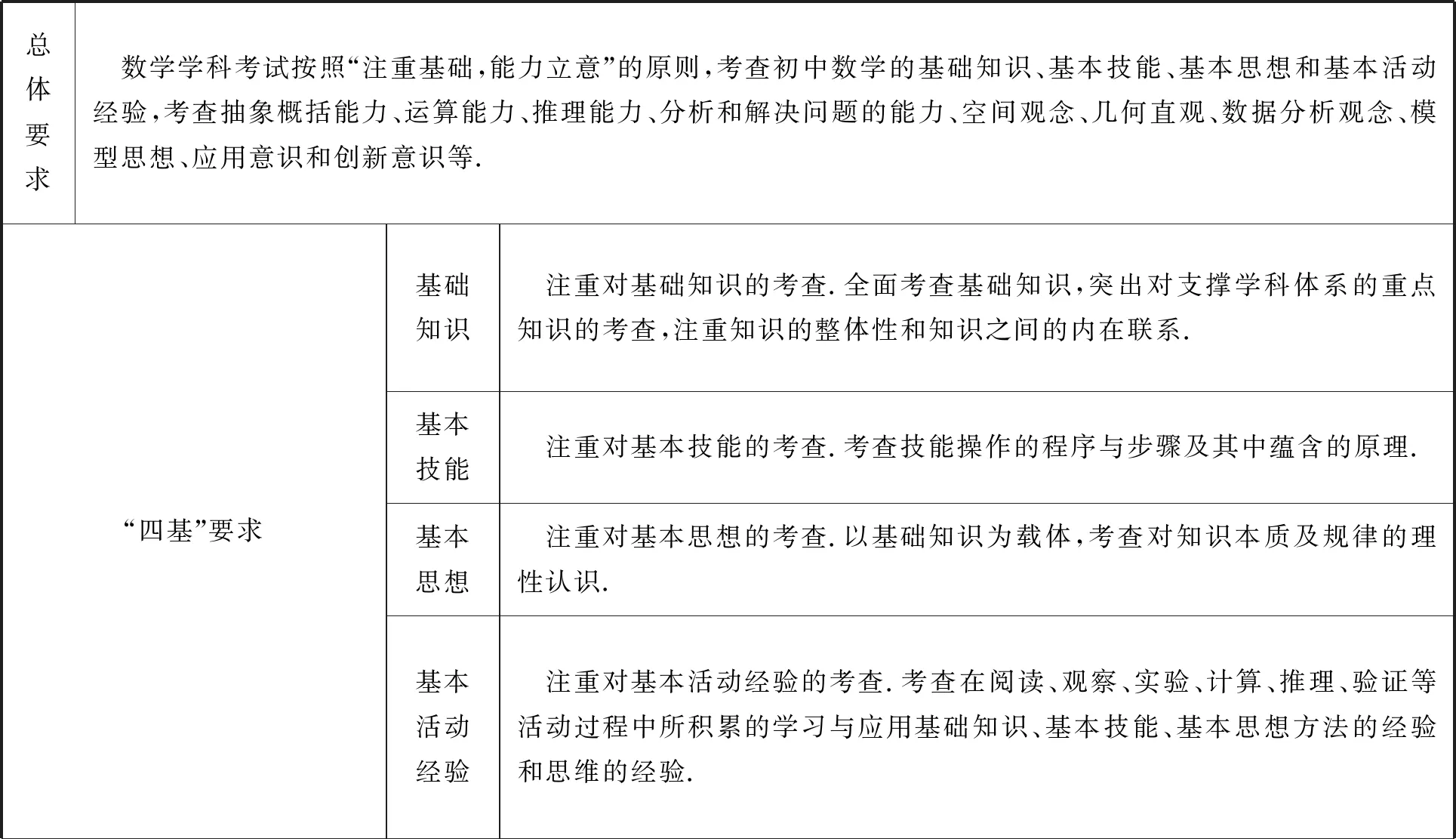
表1 数学学科评价体系的考查目标与要求(2017年版)

4 实践举例

2015-2017年，全面实施了“内容结果与学习过程”并重的评价体系.文[5]-[7]详细地介绍了“四基”、“知识体系”、“核心能力”等评价情况，此处不再过多赘述.下面以运算能力和数据分析观念为例，简述评价体系实施情况.

4.1 运算能力

对运算能力的考查，侧重于“根据特定的问题，观察、分析运算条件，探究、设计和选择合理、简洁的运算途径，解决问题”，把对运算能力考查的要求由技能运算逐步向思维运算转变，体现多思少算的思维特点.

例1(2016年14题)如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m.已知小军、小珠的身高分别为1.8m，1.5m，则路灯的高为______m.

分析试题要求计算路灯的高度.结合条件“小军身高、影长为1.8m”，观察图形，发现△BEG为等腰直角三角形；同理，△CFH为等腰直角三角形；可推理出△ABC为等腰直角三角形.故求路灯高AD就转化为求等腰Rt△ABC斜边中线AD的长度.

通过分析发现，运算能力更加注重“观察、分析运算条件”这种思维层面的考查，不是运算技巧的考查，也不是不假思索的计算.

4.2 数据分析观念

2015年数据分析观念考查要求偏向于具体实操，以经验反馈为主，缺乏统计思想的引领，对统计思维的要求不高，对调查思想、随机思想、抽样思想和量化思想四个基本统计思想的体现也不够全面.

表2 2015、2017年数据分析观念要求对比

例2(2015年25题)略

分析试题要求选择统计表或统计图，将2013-2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来，体现了“从大量数据中提取有效信息，并进行表示”的要求，主要是对数据进行操作，统计思想的考查不深刻.

例3(2017年25题)略

分析试题以“调查了解某工厂甲、乙两个部门员工的生产技能情况”为背景，呈现了统计调查的全过程：抽样方法与样本容量的确定、数据的收集、整理与描述、数据的分析、调查结论的分析与得出.对统计的过程性考查，可引导统计学习不再是单一聚焦于统计操作，而聚焦于是否理解基本统计思想，聚焦于是否具备统计思维(非确定性思维)，这就是数据分析观念的本质要求.

5 改革思考

过程性评价的育人理念源于2011版课标的育人理念，并与2011版课标育人理念是同一的.过程性评价促使教育目标由知识技能向核心素养转变，即由“学科领域知识”“听说读写基本技能”“满足人的基本日常生活需要”向“促进人的全面发展”“强调个体能积极主动，并具备一定方法获得知识和技能”“在满足生活需要之外，有助于个人追求生活目标，有效参与社会活动”转变，这种转变体现了考试与育人的关系.

5.1 促进学生全面发展

对于学生的全面发展，教师要在日常教学中依托教材、立足课堂、打开课堂，让学生在课堂中打开视野、拓宽思维、总结方法、学会应用.

例如2015年8题利用平面直角坐标系画出的故宫博物院主要建筑分布图、2016年15题百子回归图、2017年20题出入相补原理，都是依托于教材，但又不拘泥于教材，既让学生开阔了眼界，又积累了数学文化底蕴.再如2015年9题游泳馆年卡办理、2016年28题解题思路选择、2017年28题几何变换，都是解决问题的思维多样，思路不唯一，方法多样.又如2015-2017年26题，把学习一次函数、反比函数、二次函数的一般方法抽象出来，在掌握了通性通法的前提下，研究新问题，解决新问题.如2016年22题调查作业了解居住小区家庭用气量情况、2017年25题调查作业了解两部门员工生产技能情况，都是让学生实实在在的参与数学活动，在活动中不断积累经验，将数学知识真正应用到生活中，学会应用.

通过考试考宽，促进教师教宽，让学生学宽，体现学生九年的积累，关注知识面的宽度而不是知识点深度宽，向联系课堂、家庭和社会实践不断

转变，让学生真正的实现全面发展.

5.2 促进学生个性发展

在全面发展的基础上，要让不同的人得到不同的发展.不同人思考问题的出发点不一样，要尊重个性发展，尊重差异，为每个人提供不同的平台，让不同水平、不同层次的人都能充分发挥，在作答中获得成就感.

例如2015年15题预估轨道交通客运量情况、2016年12题根据图形写出满足条件的等式、2017年25题推断哪个部门生产水平较高，都是设置开放性试题，放开答案、张扬个性、驰骋思想，自圆其说、更深层次考查对知识的理解与运用，思维不趋同，培养创新能力.

5.3 把握基础

无论是学生的全面发展还是个性发展，根基都是基础知识.例如2015年19、20题关注的是基本推理能力、2016年1题关注的是基本数学工具的使用，2017年1题关注的是基本概念的理解.又如2015-2017年16题尺规作图关注的是技能操作的原理.这都是引导对于基础知识的关注，应关注基础知识的掌握而不是知识点的掌握；要关注学生获取知识的能力，而不是深挖知识点的能力.

6 结束语

现在，教学、评价和招生改革等都是现在进行时，都存在进一步研究、讨论和完善的空间.北京中考数学学科的改革也在不断地实践与完善的过程中，作者旨在通过对近三年改革进行总结与思考，与大家共同研讨，使今后的评价更加科学.若有不完善之处，请批评指正.