数学问题解答

2017年9月号问题解答解答由问题提供人给出)

2381设△ABC的三边长,对应边上的中线长,角平分线长,高线长,半周长,外接圆及内切圆半径分别为a,b,c,ma,mb,mc,wa,wb,wc,ha,hb,hc,s,R,r,则有

(天津水运高级技工学校 黄兆麟 300456)

由角平分线长公式

及正弦定理,得

注意到由面积公式

及正弦定理可推得

又∑cotBcotC=1，

那么有

另一方面,注意到由中线长,角平分线长及高线长公式可得

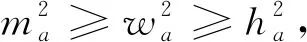
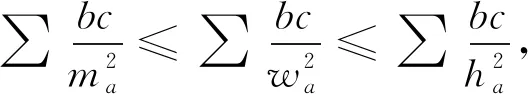
2382如图，在△ABC中，AB=BC，D是AB延长线上的一点，E是BC延长上的一点，且CE=AD．延长AC交DE于F，FG∥BE交CD于G，FH∥AD交AE于H.

求证：(1)FG=FH；(2)AF⊥GH．

(濮阳职业技术学院 纪保存 457000)

证明(1)由等高三角形的面积比等于底边之比，得

①

②

③

再由共角三角形面积比定理，得

④

①×②×③×④，并注意到

AB=BC，CE=AD，

因为FG∥BE，FH∥AD，

所以FG、FH分别是△DCE、△ADE的中位线，

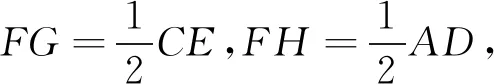
由CE=AD即得FG=FH．

(2)由题意，知

∠BAC=∠BCA，∠BAC=∠AFH，

∠BCA=∠GFA，

于是∠AFH=∠AFG，

再由(1)得AF是等腰△GFH的顶角平分线，

故AF⊥GH．

2383n是大于3的奇数，证明：n！+1与(n! -n)！+1中至少有一个是合数.

(浙江温州市区马鞍池东路1-408 陈克瀛 325000)

证明设p=n! +1是素数，

则有p| (n! ) ! +1(Wilson定理).

(1)

另一方面，

由n! =p-1 及n! -n为奇数，得

(n! ) !

=1·2 …n·(n+1 ) … (n! -1) ·n!

程颐目光晃过来的时候，粒粒觉得不好意思，于是伸出手来说：“你好。”程颐握住她的手，惊呼一声：“你的手好凉！”

=n! (p-(n!-n)) … (p-2 ) (p-1 )

=(p-1) · (hp+( -1 )n !-n· (n! -n) !)

=lp+(n! -n) ! , 其中h,l∈Z,

故 (n! ) ! +1=lp+ (n! -n) ! +1，

由此和(1)推出p| (n! -n) ! +1.

(2)

又n>3⟹n-1>2⟹ (n-1)!>2⟹n!>2n

⟹n!-n>n⟹(n!-n) ! +1>n!+1，

即 (n! -n) ! +1>p，

由此和(2) 知 (n!-n) ! +1必为合数，

这就证明了n!+1 (n! -n) ! +1中总有一个是合数 .

注意到本题中n与n! -n同为正奇数，于是由所证的结论立即得出：存在无穷多个正奇数m，使得m! +1 是合数 .

此外注意到：k|n⟹k|n!-n，由此和本题结论又推出：对于给定的正奇数k，存在无穷多个正奇数r使得(kr)!+1是合数 .

2384设a,b,c分别表示△ABC三内角A,B,C所对的边长，求证：

(1)

(河南质量工程职业学院 李永利 467000)

证明因为

所以

同理

以上三式左右两端分别相加，并利用三角形射影定理

a=bcosC+ccosB，

b=ccosA+acosC，

c=acosB+bcosA，

可得

(2)

(2)式整理即得(1)式．

2385如图，⊙O与⊙O1内切于点A，⊙O与⊙O2内切于点B，且⊙O1与⊙O2相交于点C、D，AB交CD于点T. 求证：S△TOO1=S△TOO2.

(重庆市合川太和中学 袁安全 401555)

证明如图所示.设直线AB分别交⊙O1、⊙O2于点E、F，则易知A、O、O1及B、O、O2分别共线.又设直线EO1与FO2交于点M.则易得

∠E=∠O1AE=∠OAB=∠OBA

=∠O2BF=∠F.

即ME∥O2B，MF∥O1A.

于是 四边形MO1OO2是平行四边形,

所以OM与O1O2互相平分于点N，

即NO1=NO2.

再设射线MO交AB于点T′.

①

又易得TA·TE=TC·TD=TB·TF,

②

比较①、②可知T′与T两点重合,

即，M、O、T三点共线.

所以，M、N、O、T四点共线.

故S△TOO1=S△TOO2.

2017年10月号问题

(来稿请注明出处——编者)

S△BP1Q1·S△BP2Q2=S△FA1P1·S△FA2P2．

(北京市陈经纶中学 张留杰 100020)

2387设a,b,c≥0，a+b+c=6，求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

2388如图，经过直角梯形ABCD的顶点A作斜腰CD的平行线交下底BC于点M，△DBC的外接圆ω1交直线DM于点D,G，△AMC的外接圆ω2交ω1于点C,F，△BGM的外接圆ω3交ω2于点M,E，证明：直线BE,CF,DG交于一点，且此点为△AMC的重心.

(河南省辉县市一中 贺基军 453600)

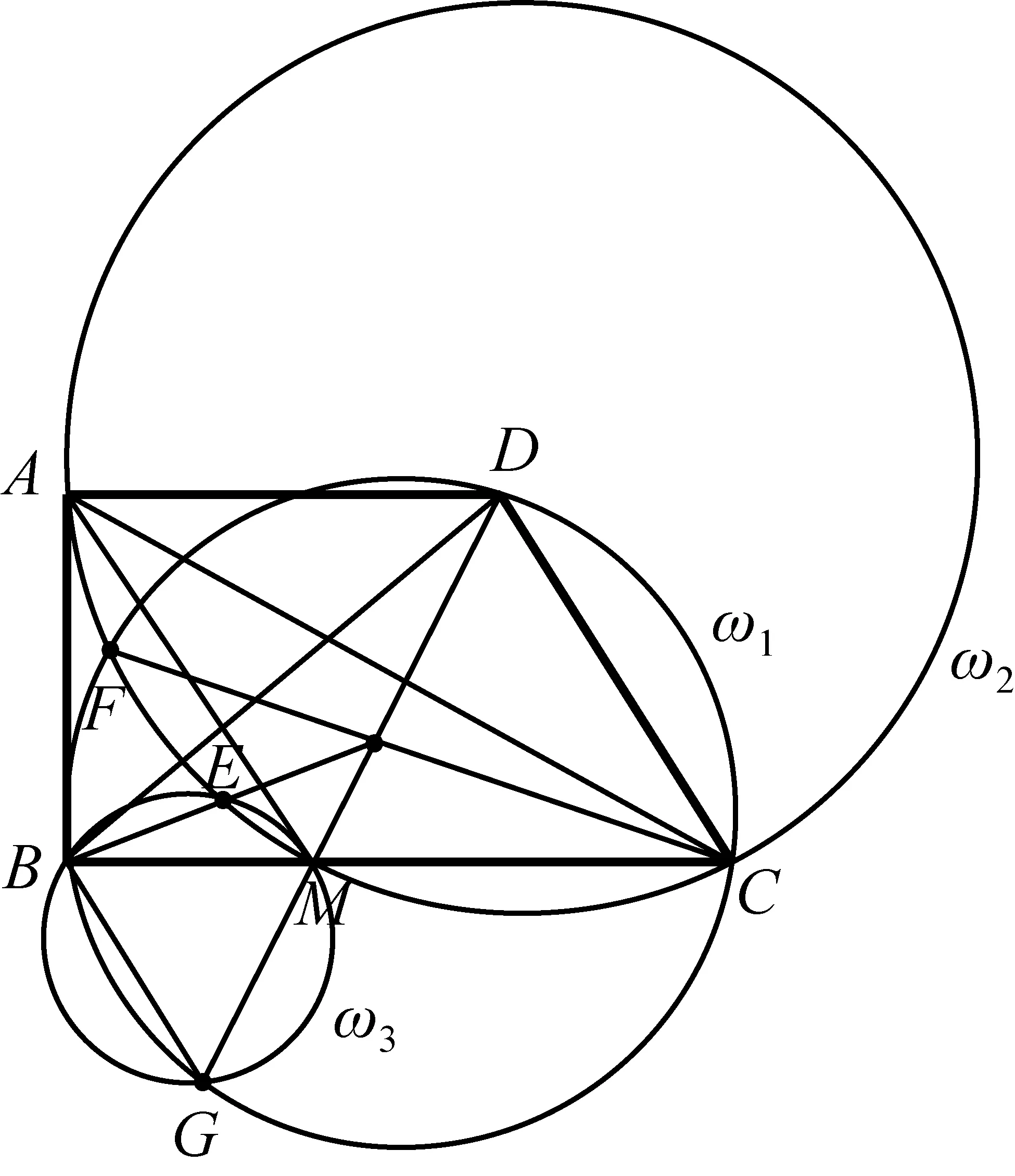
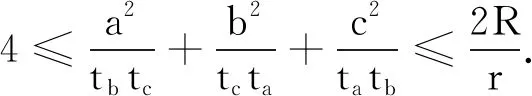
(河南质量工程职业学院 李永利 467000)

2390如图，已知⊙O上四点A、B、C、D，BA交CD于E，AC交BD于F，EF交⊙O于H、G，K为EF中点，以点A、K、C作圆交EG于T，求证：HF=TG．

(江西师范高等专科学校 王建荣 335000；温州私立第一实验学校 刘沙西 325000)