一个向量模 年年高考题

●

(浙江师范大学特级教师工作流动站,浙江 金华 321004)

一个向量模年年高考题

●曹凤山

(浙江师范大学特级教师工作流动站,浙江 金华 321004)

向量因为其双重身份在中学数学中具有广泛的应用，因而地位十分重要，也成为高考重点考查的内容之一.横看成岭侧成峰，对于向量模，视角不同就有不同的意义，因此每年涉及向量模的试题可以常考常新.

向量模；距离；夹角

向量因为其几何、代数双重身份而特殊，因为其双重身份而应用广泛，所以成为高考重点考查内容之一，其中大多涉及向量模.一个向量模，因命题的角度不同，每年都会有新颖的情境出现.下面以浙江省近十年来涉及向量模的高考试题为例，梳理高考对向量模的考查视角.

1 距离形式

向量的模就是向量长度，是连接向量起点、终点的线段长.由于起点和终点的位置、含义不同，从而出现具有不同几何意义的量，如两点之间的距离、点到直线的距离、点到平面的距离等等.

例1已知向量a≠e，|e|=1，对任意t∈R，恒有|a-te|≥|a-e|，则

( )

A.a⊥eB.a⊥(a-e)

C.e⊥(a-e) D.(a+e)⊥(a-e)

(2005年浙江省数学高考理科试题第10题)

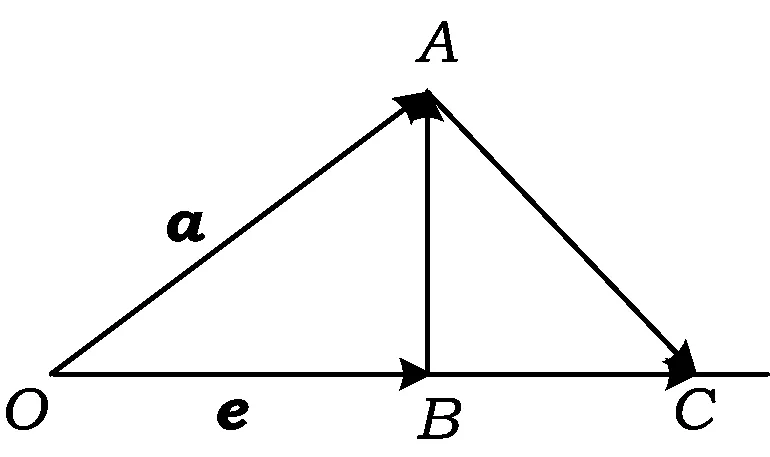
图1

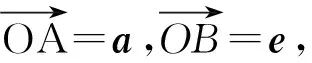
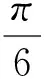
(2013年浙江省数学高考理科试题第17题)

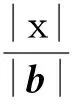
图2 图3

例3设θ为两个非零向量a，b的夹角，已知对任意实数t，|b+ta|的最小值为1

( )

A．若θ确定，则|a|唯一确定

B．若θ确定，则|b|唯一确定

C．若|a|确定，则θ唯一确定

D．若|b|确定，则θ唯一确定

(2014年浙江省数学高考文科试题第9题)

分析如图3，由|b+ta|的最小值为1，知点B到OA所在的直线的距离为1.故选B.

(2015年浙江省数学高考理科试题第15题)

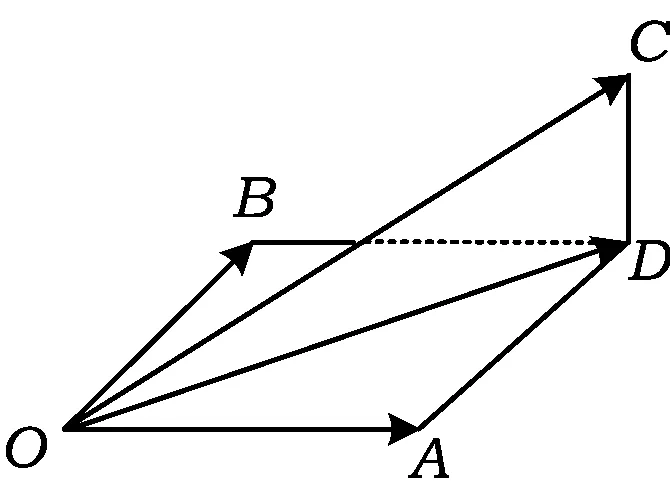
图4

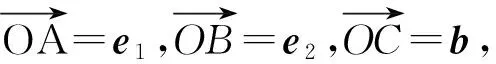
b=x0e1+y0e2+e3

2 三角形边长形式

向量的加、减运算与三角形紧密相关，向量的模通常表现为三角形边长，以向量形式表现三角形边、角之间的位置和数量关系.

例5若非零向量a,b满足|a+b|=|b|，则

( )

A．|2a|>|2a+b| B．|2a|<|2a+b|

C．|2b|>|a+2b| D．|2b|<|a+2b|

(2007年浙江省数学高考理科试题第7题)

分析如图5，由|a+b|=|b|知△OBC为以OB为底边的等腰三角形.为作图简便，把选择项中系数都除以2，这时底边上的高

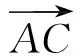
显然

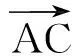
图5 图6

例6已知平面向量a，b，|a|=1，|b|=2，a·b=1．若e为平面单位向量，则|a·e|+|b·e|的最大值是______．

(2016年浙江省数学高考文科试题第15题)

分析由|a|=1，|b|=2，a·b=1易得=60°，|a·e|+|b·e|表示向量a，b在单位向量上的投影之和.如图6，OB1+B1C1=OC1，当单位向量a与b共线时，投影为OC.明显地，|OC1|≤|OC|,即当且仅当单位向量e与a+b共线时,|a·e|+|b·e|最大，此时

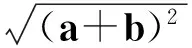
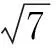
3 平行四边形的边长、对角线长形式

向量的加、减运算与平行四边形密切相关，向量的模通常表现为平行四边形的边长、对角线长等形式，以向量形式体现平行四边形中的位置、数量关系.

( )

A.min{|a+b|,|a-b|}≤min{|a|,|b|}

B.min{|a+b|,|a-b|}≥min{|a|,|b|}

C.max{(a+b)2,(a-b)2}≥a2+b2

D.max{(a+b)2,(a-b)2}≤a2+b2

(2014年浙江省数学高考理科试题第8题)

分析根据向量加法的平行四边形法则与减法法则，容易证明

则(a+b)2,(a-b)2中至少有一个不小于a2+b2，即

max{(a+b)2,(a-b)2}≥a2+b2.

下面一道高考题更明显地体现出平行四边形(正方形)对角线与一组邻边的关系.

例8设向量a,b,c满足a+b+c=0,(a-b)⊥c,a⊥b,若|a|=1,则|a|2+|b|2+|c|2的值是______.

(2006年浙江省数学高考理科试题第13题)

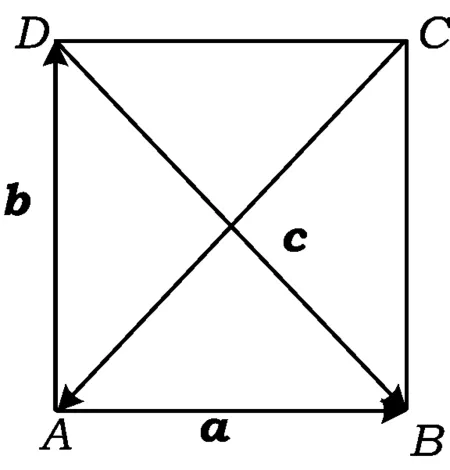
图7

分析如图7，由a⊥b知四边形ABCD为矩形，又由a+b+c=0，(a-b)⊥c,知四边形ABCD为正方形，从而

c2=2|a|2，

故

|a|2+|b|2+|c|2=4.

下面这道高考题是典型的考查平行四边形对角线与边长关系的问题.

例9已知向量a，b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______，最大值是______.

(2017年浙江省数学高考试题第15题)

分析从向量运算的几何意义出发，易得

|a+b|2+|a-b|2=2(|a|2+|b|2)=10,

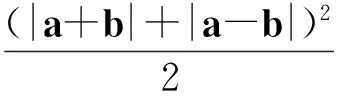
4 圆的弦长形式

除了以三角形、平行四边形为背景，向量的模还常常以圆为背景，涉及圆的弦、半径以及直径等.

例10已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0,则|c|的最大值是

( )

(2008年浙江省数学高考理科试题第9题)

图8 图9

例11已知平面向量α,β(其中α≠0,α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是______.

(2010年浙江省数学高考理科试题第16题)

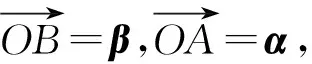
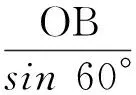
从而

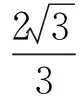
5 数量积的另一形式

向量的模、向量的数量积都是向量部分的重要量，这两个量之间除了在数量积中的联系之外，还有其他关系吗？

(2012年浙江省数学高考理科试题第15题)

分析因为AM=3，MB=MC=5，所以

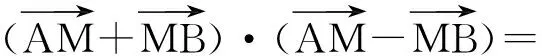
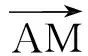
实际上，本题体现了一个一般性的关系式：

写成一般的关系式为

这就是大家所说的“极化恒等式”.该式说明:向量的数量积可以由向量和、差运算的模表示，该式沟通了向量的数量积与线性运算之间的关系，有着广泛而重要的应用.

( )

A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

(2013年浙江省数学高考理科试题第7题)

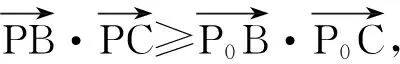
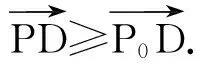
(2016年浙江省数学高考理科试题第15题)

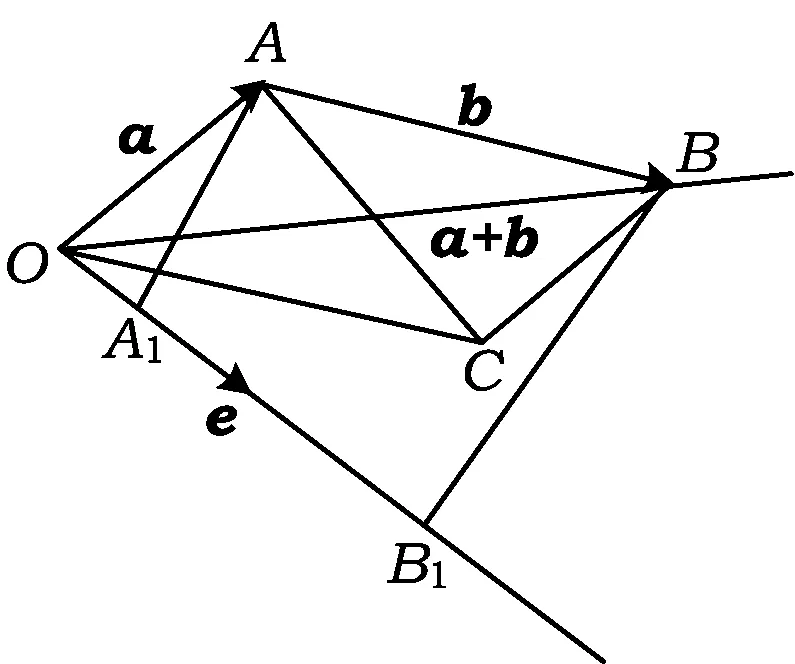
图10

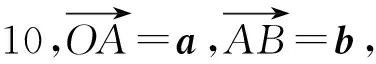
(a+b)2+(a-b)2=

2(a2+b2)=10.

则(a+b)2有最大值6，这时(a-b)2取到最小值4，故

当且仅当单位向量e与向量a+b共线时,等号成立.

[1] 曹凤山. 年年考向量 岁岁数与形——浙江省自主命题以来向量试题特点评析[J].中学教研(数学),2013(4):37-39.

[2] 曹凤山.数学教学 把根留住——2015年浙江省数学高考试题解读[J].中学教研(数学),2015(8)：1-4.

2017-09-26

曹凤山(1967-)，男，山东菏泽人，山东省特级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)12-43-04