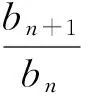一阶非线性递推关系问题的结构分析
——函数观点下的处理模式探讨
●
(嵊州中学,浙江 嵊州 312400)
一阶非线性递推关系问题的结构分析
——函数观点下的处理模式探讨
●俞海东
(嵊州中学,浙江 嵊州 312400)
在高中数学教学中,数列往往是高考和竞赛备考的重点内容之一,能否顺利解决此类问题是体现学生数学水平高低的关键.文章从数列递推式对应的函数关系式出发,利用函数图像研究对应关系的单调性、取值范围、周期性等.
递推函数关系;数列图像;数列单调性;数列不动点
数列作为特殊的函数,其特点有:1)定义域与值域往往是同一个且离散的;2)对应函数关系式的图像倾斜率是否比1大决定数列的单调性;3)函数的不动点决定数列中的项的变化方向;4)对应的函数关系式类型决定所求通项的类型.
由此,数列对应的函数关系结构决定了数列问题的处理方法,对应关系式有一次式结构、分式结构、二次结构等.接下来笔者将探讨此类数列的一般处理模式:
1 利用数列的图像研究数列的性质
数列是特殊的函数,作出数列的图像对于此类问题的解决帮助很大[1].

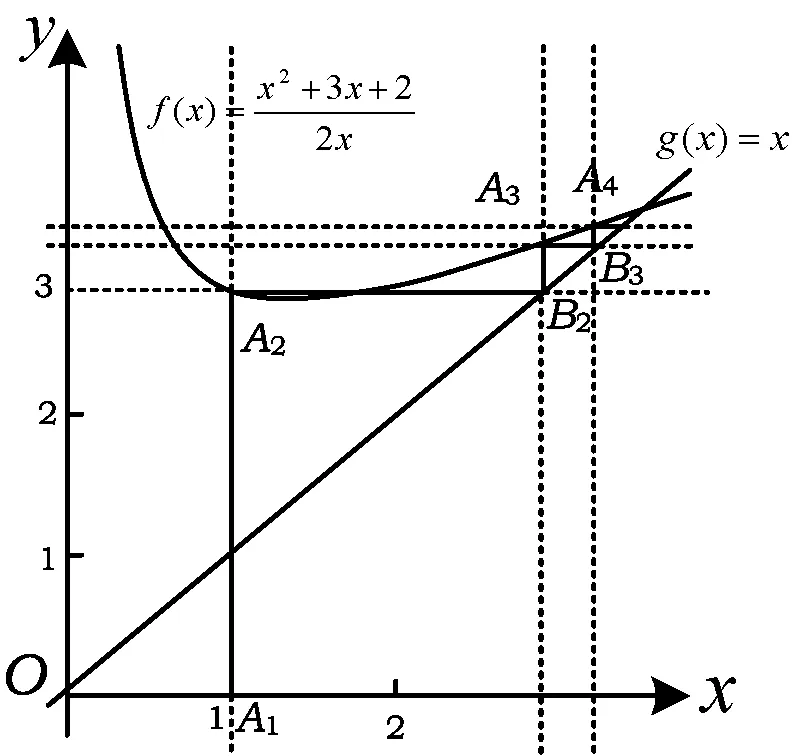
图1

点评将递推式中所表示的函数对应关系用图像直观地表达[1],利用直线y=x对an的自变量转化,容易观察得到数列的性质.
2 利用不动点理论简化递推关系式
模式1已知数列首项a1和递推式an+1=f(an),提炼an+1与an的函数关系式为y=f(x),若方程f(x)=x有根x0(此根为函数y=f(x)的图像与函数y=x的图像交点的横坐标),一般将递推式变形为:
模型1an+1-x0=f(an)-x0,令bn=an-x0,代入消元得bn,问题转化为研究数列{bn}.
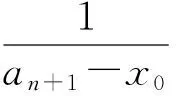
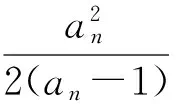
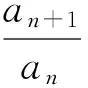
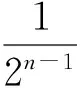
3)略.
(1984年全国数学高考试题第8题)
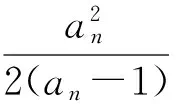

令f(x)=x,求出不动点x=2,将递推式变形为

再倒数变形为
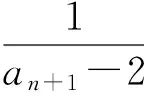



2)证明转化为:若bn≥1,则bn≥2n-1.因为

所以

又b1≥1,从而
bn≥2n-1.
点评根据一阶递推式得到函数关系式,求出不动点之后,对递推式一般会有两种变形:1)直接减去不动点;2)减去不动点并进行倒数,以达到简化递推式的目的.
3 利用求函数值域的方法来研究数列的项的范围
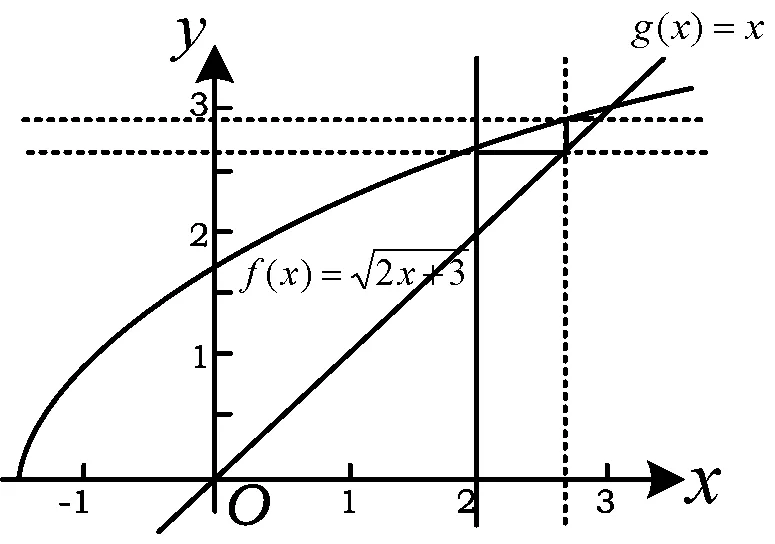
模式2已知数列首项a1和递推式an+1=f(an),求证:an 提炼an+1与an的函数关系式为y=f(x),用数学归纳法证明an 1)求证:an 图2 2)由题意Sn=a1+a2+a3+…+an, 则 用数学归纳法证明: ①当n=1时,a1=2,a1≥3-1显然成立. 只需证 即 亦即 化简得 又k∈N,上式显然成立. 模式3已知数列首项a1和递推式an+1=f(an),求证:an 提炼an+1与an的函数关系式为y=f(x),an 分析要证an+1>an,利用等式消元只需证 即 ③由情形①和②可知,结论成立. 点评an+1与an的函数关系式为y=f(x)且具有导数,若f′(x)>1,则数列{an}单调递增;若f′(x)<1,则数列{an}单调递减. 例5设数列{an}满足|an+1-2an|=2,|an|≤2,其中n=1,2,3,…,证明:若a1为有理数,则从某项后{an}为周期数列. (2016年浙江省高中数学竞赛试题第13题) 分析将递推关系式中的绝对值打开,得到an+1=2an±2,结合|an|≤2,得到 上述递推式中表示的对应关系为 图3 作出其图像(如图3所示),并作出y=x的图像.在递推式中取n=1,根据对应关系a2=f(a1),在x轴上取数a1对应的点A1,过A1作x轴的垂线,与函数y=f(x)的图像相交,交点为A2(其纵坐标为a2),过A2作y轴的垂线,与直线y=x相交,交点为B2(其横坐标为a2),与函数y=f(x)的图像交于点A3(其纵坐标为a3);同理,过此点A3作y轴的垂线,与直线y=x相交,交点为B3(其横坐标为a3),过B3作x轴的垂线,垂足为A4,其横坐标为a4,依次进行,可以得到a4,a5,…,an,这些项只能在如图3所示的一块平面区域内变动. 模式4已知数列首项a1和递推式an+1=f(an),求证:an+1>F(an)(其中F(an)是对an+1的一个放缩). 提炼an+1与an的函数关系式为y=f(x),an+1>F(an)⟺f(an)>F(an),即解不等式f(x)>F(an),解出x的范围A,再证明an∈A,问题转化为前面的模式1中的问题. 因为an>0,所以 将代数式an+1-an理解成第n+1项与第n项的距离,由累加法得到 an-a1= (an-an-1)+(an-1-an-2)+…+ (a3-a2)+(a2-a1), 即第n项与第1项的距离等于第n项与第1项之间的前后两项距离之和. 分析已知条件可表达为 an+1-an≤an+2-an+1, 此式可理解为第n+1项与第n项的距离不大于第n+2项与第n+1项的距离. 图4 图5 an+1-an+2≤an-an+1, … 从而Sk=a1+a2+a3+…+ak> 点评放缩模式:已知数列首项a1和递推式an+1=f(an),若考虑裂项放缩: an+1-an=f(an)-an=F(an), 则an-a1= (an-an-1)+(an-1-an-2)+…+ (a3-a2)+(a2-a1)= F(an-1)+F(an-2)+F(an-3)+…+ F(a2)+F(a1), 再根据y=f(x)的单调性,结合项an的范围进行放缩. 即由第n项与第1项的比值距离等于第n项与第1项之间的前后两项比值距离之和. (1984年全国数学高考试题第8题第3)小题) 分析由递推式 可提炼an+1与an的函数关系式为 令f(x)=x,求出不动点为x=2,将递推式变形为 b1 从而 (2b1+2)nb1, 亦即 (1) 且 点评放缩模式:已知数列首项a1和递推式an+1=f(an),考虑裂项放缩 F(an-1)·…·F(a2)F(a1), 再根据y=f(x)的单调性结合项an的范围进行放缩. 数列问题作为数学高考中的重要内容之一,如何用函数的方法统一高效地帮助考生思考此类问题,是高三复习备考的重点之一.希望拙文能给大家提供一点帮助,不当之处,请批评指正. [1] 俞海东.高中数学思维自学课程[M].上海:华东理工大学出版社,2017. 2017-07-15 俞海东(1979-),男,浙江嵊州人,中学一级教师.研究方向:数学思维. O12 A 1003-6407(2017)12-26-05
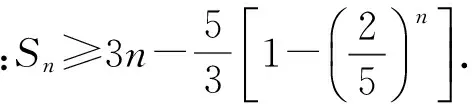

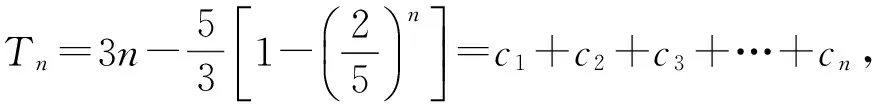

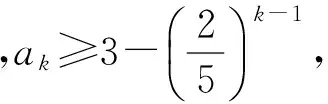
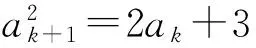
4 将数列单调性问题转化为前面的数列的项的范围问题

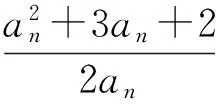
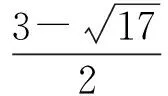

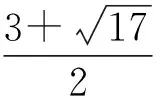
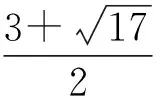
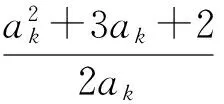


5 利用数列中项为有理点所具有的封闭性
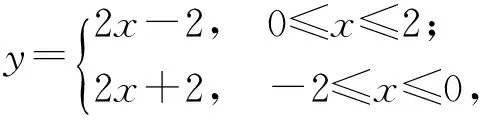


6 将数列前后两项的代数式大小问题转化为前面的数列的项的范围问题
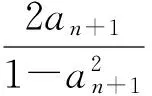


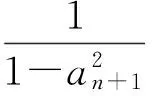


7 利用两项之间距离的概念
7.1 利用差值距离

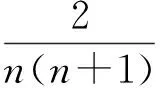
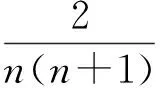







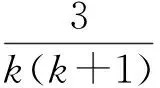




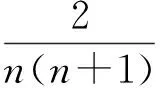
7.2 利用比值距离