简化解析几何运算量的两个视角

●

(姜堰第二中学，江苏 泰州 225500)

简化解析几何运算量的两个视角

●朱传美

(姜堰第二中学，江苏 泰州 225500)

如何简化解析几何的运算量一直是解析几何研究的重点.此类文献常见于各类期刊，其中第一篇参考文献中的处理方法就有近20种，对高三的复习具有非常高的参考价值.方法虽多，但不能揭示问题之根本，学生只会生搬硬套.鉴于解析几何的代数与几何双重身份，文章提出两个视角：几何视角和代数视角，能较好地解决上述困惑.

简化运算；几何视角；代数视角

文献[1-3]均就简化解析几何运算量的策略进行了系统地归纳和例解，3位教师针对各自文中所列举的不同情形进行了精辟的文字概括，如文献[1]给出了5种策略：设而不求、巧用几何性质、合理翻译条件、利用常见结论、争取整体替代，各种处理方法加起来近20种，对高三的复习具有非常高的参考价值.这么多方法的掌握甚至熟练运用，对教师来说还能行，而对于学生就显得困难多了.

方法虽多，若不能揭示问题之根本，则学生只会生搬硬套，只知其然，不知其所以然，遇到新题目，还是不能处理.众所周知：解析几何的根本是用代数方法处理几何问题，因此解析几何兼有代数与几何的双重身份，鉴于此，我们认为：简化解析几何运算量有两个视角，即几何视角和代数视角.

1 几何视角

几何视角即从几何的角度处理解析几何问题.因为平面解析几何首先是几何，所以在处理解析几何问题时，首选几何视角，通过几何视角，能够挖出题中蕴含的轨迹或几何性质，从而简化运算.

1.1 几何视角挖掘所蕴含的轨迹

例1在平面直角坐标系xOy中，已知直线y=x+2与x轴、y轴分别交于点M,N，点P在⊙C:(x-a)2+y2=2上运动，若∠MPN恒为锐角，则实数a的取值范围是______.

分析此题虽然是一道填空题，但若条件“∠MPN恒为锐角”处理不好，将带来繁琐的运算.我们知道∠MPN恒为锐角即0°<∠MPN<90°，而当∠MPN=90°，即MP⊥NP时，点P在以MN为直径的圆上，从而挖出蕴含的轨迹，达成问题的优化解决.

亦即

解得

1.2 几何视角挖掘所蕴含的几何性质

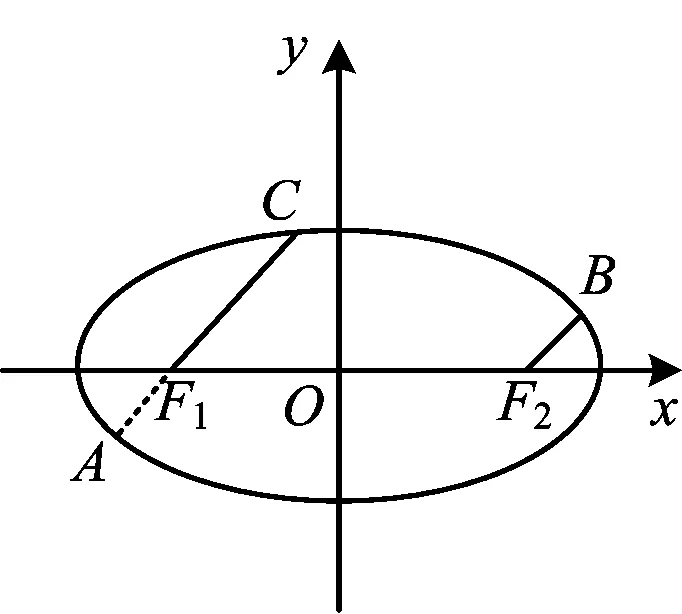
图1

1)求椭圆E的方程；

2)过点F1,F2分别作两条平行直线F1C和F2B交椭圆E于点C,B(点C,B均在x轴上方)，且F1C+F2B等于椭圆的短轴长，求直线F1C的方程.

分析第2)小题中F1C+F2B=2b是难点，因为线段F1C,F2B在不同的直线上，若各自与椭圆联立方程组求出线段F1C,F2B的长，则将带来很大的运算量，这需要我们从几何角度来挖掘几何性质，以避开繁琐运算，达成问题的优化解决.

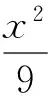
2)延长CF1交椭圆E于点A,因为直线F1A,F2B关于坐标原点(0,0)对称,所以点A,B关于坐标原点(0,0)对称，F1A=F2B,且

CA=CF1+F1A=CF1+F2B=2b=2.

得

从而

(1)

又CA=CF1+F1A=a+ex2+a+ex1=

(2)

几何视角能从几何角度挖掘题目所蕴含的轨迹或几何性质，从而揭示问题本质，简化运算；通过几何性质可以进行适当转化，简化运算，最终实现问题的优化解决，从而达到简化运算的目的.

2 代数视角

平面解析几何的精髓是用代数方法处理几何问题.代数视角即从代数的角度处理解析几何问题，通过代数视角，能够挖出题中蕴含的轨迹方程或代数关系，从而简化运算.

2.1 代数视角挖掘所蕴含的轨迹方程

图2

1)求椭圆E的标准方程；

2)若直线l1,l2的交点Q在椭圆E上，求点P的坐标.

(2017年江苏省数学高考试题第17题)

分析此题为2017年江苏省数学高考试题第17题，重点考查圆锥曲线的运算处理能力.第2)小题是核心，一些考生由于找不到好的简化运算的途径而陷于困境，那我们能否通过运算发现动点P的轨迹方程，走出运算的困境，从而达成减少运算量的目的.

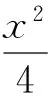
2)因为F1P⊥F1Q,F2P⊥F2Q,所以

∠PF1Q=∠PF2Q=90°,

即

∠PF1Q+∠PF2Q=180°,

从而点F1,F2,P,Q在以PQ为直径的圆上.设圆心为C,则C为线段PQ的中点且在线段F1F2的中垂线(y轴)上，可设C(0,t),P(x1,y1)(其中x1>0,y1>0)，则Q(-x1,2t-y1).又点P,Q均在椭圆上,从而

当-y1=2t-y1，即t=0时，代入上述方程组，得

此方程组无解.

当y1=2t-y1，即t=y1时，代入上述方程组，得

解得

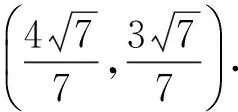
评析本解法旨在通过代数运算找到点P所满足的新的轨迹，而点P的坐标即为新的轨迹方程与点P所在的原椭圆方程的交点.通过上述解法可知：符合题意的点P的新的轨迹方程为：x2-y2=1.

2.2 代数视角挖掘所蕴含的代数关系

图3

例4如图3，某学校在平面图为矩形的操场ABCD内进行体操表演，其中AB=40,BC=16,O为AB上一点，且BO=8，线段OC,OD,MN为表演队列所在位置(点M,N分别在线段OD,OC上)，点P为领队位置，且点P到BC,CD的距离均为12，记OM=d，我们知道当△OMN面积最小时观赏效果最好.

1)当d为何值时，P为队列MN的中点？

2)怎样安排M的位置才能使观赏效果最好？求出此时d的值.

分析显然，建立坐标系能较好地解决此题，第2)小题若通过直线与直线联立方程组直接求得点M,N的坐标，再表示出S△OMN，则将带来一定的运算量；若能挖掘出点M,N,P坐标之间的代数关系，则能简化运算，达成问题的优化解决.

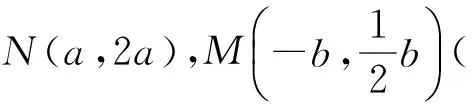
故

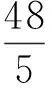
2)因为点M,N,P共线，所以

即

从而

得

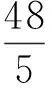
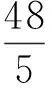
代数视角能从代数角度挖掘题目所蕴含的轨迹方程或代数关系，通过轨迹方程可以揭示问题本质，简化运算；通过代数关系实现已知与待求的沟通，简化运算，最终实现问题的优化解决，从而达到简化运算的目的.

我们认为：揭示数学问题的本质才是解决数学问题的上上之策，解析几何同时具有几何和代数的双重身份，必然从几何与代数这两个视角考虑问题，解决问题.

[1] 谢宁.减少解析几何运算量的若干策略[J].中学数学教学参考(下旬)，2016(1/2)：88-99.

[2] 王萍.巧构妙用，简化解几运算[J].上海中学数学，2013(1/2)：48-50.

[3] 林明成.简化解几运算的十二法[J].中学数学研究，2010(9)：38-41.

2017-10-09

江苏省泰州市“十三五”教育科研规划2017年度立项课题(tjkyblx2017/033)

朱传美(1976-)，男，江苏兴化人,中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)12-13-03