近年高考数学文化试题的综述

【摘 要】数学文化试题近年来在高考中一直有所体现。对这些试题进行统计，可以得出部分出题规律。对教材中并未涉及的试题背景进行归纳，有助于教师有针对性地指导学生复习迎考。

【关键词】数学文化；高考试题；备考策略；试题统计

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2017）75-0041-04

【作者简介】罗文军，甘肃省秦安县第二中学（甘肃秦安，741600）教师，二级教师。

一、数学文化的内涵

顾沛在《数学文化》一书中从课程角度解释了数学文化内涵：简单说，是指数学的思想、精神、方法、观点，以及它们的形成和发展；广泛些说，除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等。

2003年版的《普通高中数学课程标准（实验）》中提出的新课程标准理念之一是体现数学的文化价值。但在具体教学中，大多学校由于高考没有对数学文化提出要求，对课本中涉及数学文化的阅读与思考、探究与发现以及人教A版选修3-1《数学史选讲》等内容在教学中都没有开展，这造成了不知道《九章算术》的高中生大有人在。2017年修订后的高考数学考纲增加了对数学文化的要求——展现数学的科学价值和人文价值。这对高中教学具有很好的导向作用。以数学文化为背景命题，为高考注入了新的活力。历年高考题中不乏渗透数学文化的试题，这类试题凝结了高考命题专家的心血和智慧，本文对这类试题加以综述与分析。

二、数学文化试题的统计与分析

以下是近5年高考全国卷（见表1）、湖北卷2009～2017年（见表2）、其他省份2007～2017年（见表3）数学文化试题分布统计表。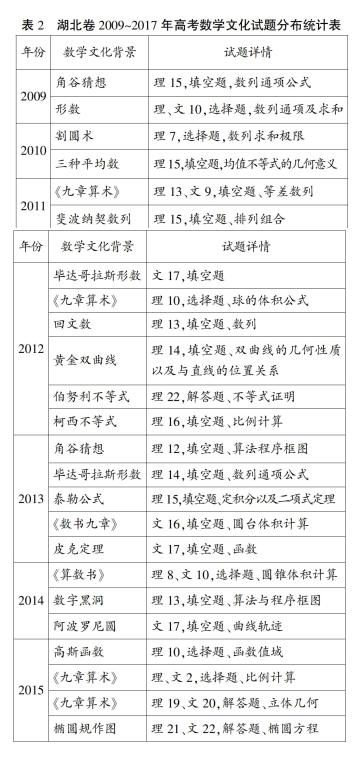

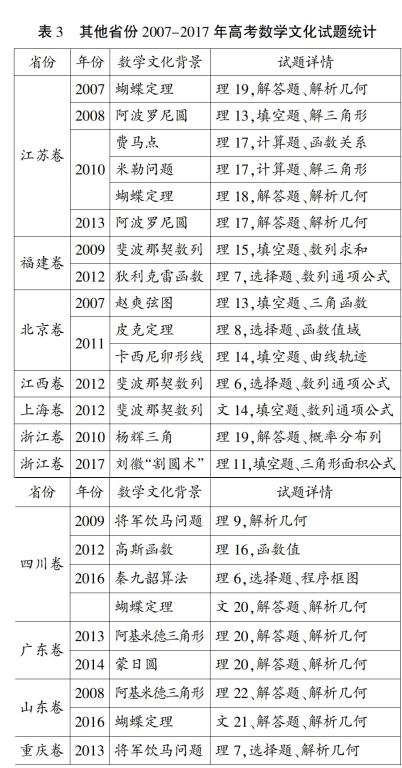
从上表不难看出，从2009年到2017年间，湖北卷出现的数学文化试题总数目较多，类型五花八门。全国卷在2013年到2017年间，在Ⅰ卷或Ⅱ卷中相应设置了一些数学文化试题。无论从全国卷、湖北卷，还是其他省高考试卷来看，高考数学文化试题主要出现在理科试卷中。从题型上来看，数学文化试题主要以小题的形式出现在选择题和填空题里面，解答题中较少。从所考查的知识点上来看，以我国经典数学名著《九章算术》《数书九章》《算法统宗》和《算数书》中问题为背景的文化试题，主要考查立体几何、数列、算法程序框图等知识内容。以“阿基米德三角形”“蝴蝶定理”为背景的试题出现在解答题里面，主要考查解析几何的知识。

其次，有的数学文化试题直接给出了背景，有的没有给出背景。这些数学文化试题，有的出自我国经典古名著，有的出自数学名题，有的以著名图形为背景。既考查了高中数学主干知识，也考查了学生的创新意识，关注了考生的人文情怀。这类试题丰富了高考数学命题的素材，使高考试题充满了生机和灵气，也增强了考生的文化自信。在2017年高考数学考试大纲修订后，2017年全国Ⅰ卷、全国Ⅱ卷、浙江卷都相应地设置了数学文化试题，我们可以大胆推断，在2018年高考中，将有更多的省份、地区设置数学文化试题，数学文化试题所占的比例也将会有所增加。

三、数学文化试题背景归类

1.源自古代数学名著的文化试题。

以《九章算术》《算法统宗》《数书九章》《算数书》等古代数学名著为背景的试题可以归为此类。其中《九章算术》出现的次数最多。《九章算术》是在相当长的一段时间里经过众多学者的收集、删补而编纂的中国古代经典著作，成书于约公元前1世纪。《九章算术》涉及农业、商业、工程、测量、方程解法以及直角三角形的性质等知识。它是中国古代数学知识的缩影，全书包含246道应用问题，分成九章编写：方田，粟米，衰分，少广，商功，均输，盈不足，方程，勾股。《九章算术》作为“算经十书”之首，其中包含了数形结合思想、算法化思想、极限思想、模型化思想。它们在很大程度上反映了我国传统数学的基本思想方法，对于培养学生的数学能力有着重要的意义。

2015年新课标全国卷Ⅰ理科第6题源于《九章算术》第五章《商功》之[二五]，该题将古代文化“依垣”和现代数学概念“圆锥”结合，试题新颖，贴近生活，考查了圆锥的性质和圆锥的体积公式。对弘扬中国数学文化，培养学生的爱国情操和认识中华古典文化有着深刻的教育意义。

除了《九章算术》，以其他古代数学名著為背景的试题也零散出现于过往的考题中。例如，2017年全国新课标Ⅱ卷理科第3题以《算法统宗》中的问题为背景，考查了等比数列的定义、通项公式和前n项和公式。

2.源自著名图形。

中国古代图形的创意化应用来源于对文字符号的意象化创意，其中最著名的是太极图。它是中国古代人智慧的结晶，也体现了中国古代文化的博大精深。太极图的原型为两条相互追逐的鱼，逐渐演化为现在所见的标准太极图。标准的太极图被S线分为黑白两个区域，黑为阴，白为阳，同时黑色区域里有一白点称为阴中阳，白色区域里一黑点称阳中阴。太极图集美学与哲学于一体，凝聚了中华传统文化的思想精髓，概述了宇宙万物的规律，体现了精深的美学思想，反映了中华民族思维方式和文化观念。2017年全国新课标I卷理科第2题以太极图的对称美为背景，考查了与面积有关的几何概型概率的计算。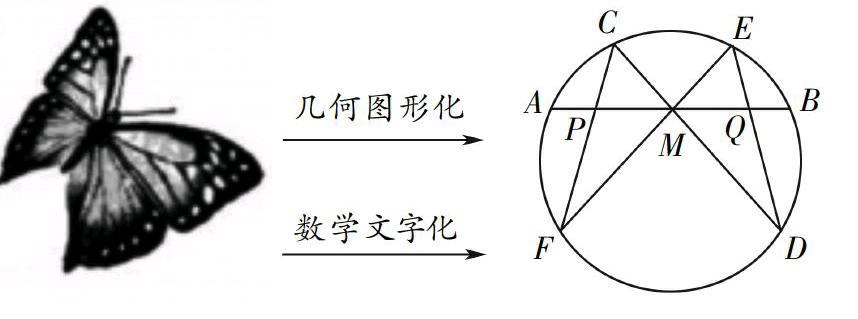endprint

高考中还有源自著名图形赵爽弦图、杨辉三角、毕达哥拉斯形数的文化试题。

3.源自名题。

以祖暅原理、刘徽“割圆术”、阿波罗尼圆、斐波那契数列、勃罗卡点、将军饮马问题、米勒问题、皮克定理为背景的文化试题，都可以看成源自历史名题。

刘徽是我国魏晋时期的数学家，他提出的“割圆术”是求圆周率的一种著名算法。割圆术中提出的“割之弥细，所失弥少，割之又割至于不可割，则与圆合体而无所失矣”可视为中国古代极限思想的论述。

2017年高考浙江卷理科第11题以刘徽割圆术为依托，考查了利用三角形面积公式求圆的内接正六边形的面积，弘扬了我国传统的数学文化，有助于提高学生的数学素养。人教A版数学必修3第45页“阅读与思考”中专门介绍了“割圆术”。

4.以著名猜想为背景的文化试题。

以“角谷猜想”“四色猜想”为背景的试题可以看成源自著名数学猜想的试题。

“角谷猜想”，又称“冰雹猜想”，内容为：任意给一个自然数n，如果它是偶数，就将它除以2，即将它变成；如果它是奇数，就将它乘以3再加上1，即变成3n+1。对任意的一个自然数，施行这种演算手续，经过有限步骤后，最后结果必然是自然数1。2009年湖北卷理科第15题以角谷猜想为背景，考查了数列的递推公式和分类讨论思想。

5.体现数学之美的数学文化试题。

典型的是以蝴蝶定理为背景的高考数学文化试题。

图1中，左边是一只漂亮的蝴蝶，几何图形化、数字化后得到一个漂亮命题：设AB是圆O的一条弦，过AB的中点M，作两条弦CD和EF，设CF、ED与AB分别交于P、Q两点，则MP=MQ。人们将其称之为“蝴蝶定理”。蝴蝶定理的证明目前已有60多种不同的方法。2016年山东卷文科第21题以椭圆中的蝴蝶定理为背景，考查了椭圆的方程、椭圆中的定值问题、直线与椭圆的位置关系、椭圆中的最值，也考查了考生的推理论证能力和运算求解能力。

体现数学之美的还有以黄金分割比为背景的数学文化试题。2012年高考湖北卷理科第14题以黄金双曲线为载体，考查了直线与双曲线的位置关系，双曲线的几何性质以及数形结合的思想。

6.体现数学与其他学科联系的数学文化试题。

（1）以黑洞数为背景的文化试题（体现数学与天文学联系）。

“黑洞”是天文学中的一个概念，数学中也存在类似天文学上的黑洞——数字黑洞。数字黑洞其实并不是真正意义上的黑洞。人们对某一自然数，给定一个特定的运算规则后，经过一步或者几步运算之后其结果会循环出现。人们形象地把这一现象称为数字黑洞。2014年湖北卷理科第13题的背景是数学黑洞问题，考查了程序框图的运算，也考查了学生的推理论证能力和创新意识。

（2）以回文数为背景的文化试题（体现数学与文学联系）。

“回文”是指无论顺拼（写）或倒拼（写）都完全一样的词、诗歌、句子或数字等。在数学里，无论从左到右还是从右到左都是同一个数的正整数称为回文数。以“回文数”命制试题，体现了数学背景下的对称之美。2012年湖北卷理科第13题以有趣的回文数为背景进行命制。该题直接给出回文数概念来考查学生的排列组合知识以及数学学习和理解能力，侧重考查学生利用排列组合知识分析解决问题的能力。该题通过创设新颖有趣的背景，进而在新的知识背景中考查排列组合知识的掌握及应用。

四、数学文化试题的教学策略

首先，每一个数学知识都有其背景和文化，因此在授课的时候，教师可以提前让学生搜寻某一知识的背景或者创作这个知识或公式的故事。让学生在故事中体会数学的魅力和文化。在以后的学习中，学生潜移默化地受这些文化所影响，自然而然地就有了一定的思维能力，从而提高学生的学习能力。例如在“基本不等式≤”的教学中，可以安排学生课前收集赵爽弦图的知识并整理成小短文，课堂上讲到赵爽弦图时，让做了准备的学生发言，介绍自己搜集到的成果。

其次，部分高考数学文化试题在课本中能找到影子，例如秦九韶算法、更相减损术出现在人教版数学必修3的正文中，伯努利不等式出现在选修4-5的正文中，高斯函数、阿波罗尼圆、角谷猜想出现在教材习题中，祖暅原理、刘徽割圆术、斐波那契数列出现在教材阅读与思考或探究与发现栏目中。在具体教学中，教师可以设置一些数学文化习题与这些数学文化知识相配套。

再次，在高一、高二的教学实践中，教师可以自己仿照历年高考数学文化试题根据《九章算术》等经典名著中的经典问题编制立体几何、数列或者程序框圖文化试题。教师可以自己上网搜集阿基米德三角形的性质等知识点，根据性质自己改编一些试题，以便学生在学习中使用。

最后，在高三复习教学的二轮复习专题中，要做到回归课本，挖掘课本中的数学文化素材。教师可以专门精心挑选历年高考真题、2017年和2018年各省模考试题中的经典数学文化试题编制数学文化专题，让学生通过做题，加深对数学文化知识的理解。在具体的教学中，教师可以收集这些文化试题的背景知识制作成课件，借助多媒体进行演示，这样不但可以提高学生的学习兴趣，也可以培养学生的创新意识。

【参考文献】

[1]顾沛.数学文化[M].北京：高等教育出版社，2008.

[2]陈昂，任子朝.突出理性思维，弘扬数学文化[J].中国考试，2015（03）.

[3]梅磊，史嘉.例谈数学文化融入高考试题的意义和途径[J].中学数学教学参考：上旬，2015（1～2）.endprint