基于局部结构张量-互信息的多模态图像配准*

张莉 李彬 田联房 李祥霞

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)

基于局部结构张量-互信息的多模态图像配准*

张莉 李彬†田联房 李祥霞

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)

互信息测度仅考虑了图像全局一致的灰度统计特性而忽略了空间结构信息和图像灰度统计的局部性特点.为克服以上缺点，提出了一种基于局部结构张量-互信息新测度的配准方法. 所提出的新测度充分考虑了图像邻域的结构信息, 将结构越强的位置赋予较大的度量值, 使得全局极值的区别性加强, 减少了配准过程中陷入局部极值的风险, 提高了配准成功率, 增强了配准的鲁棒性. 采用模拟脑图像和临床图像进行了配准试验，结果表明, 与基于互信息和局部互信息的配准方法相比, 该方法配准成功率平均提高了50%以上, 配准鲁棒性显著增强.

图像配准;相似性测度;局部结构张量;互信息

当前,图像配准的相似性测度主要分为基于特征和基于灰度的相似性测度[1].基于特征的配准方法计算量小、运算速度快,但不易自动计算,易受到标识人主观经验影响,使得提取的特征产生很大的误差,将严重影响图像配准的结果.基于灰度的配准方法直接使用图像的灰度信息进行计算,避免了特征提取给图像配准带来的误差,因而它成为了目前研究最多、应用最广的图像配准方法,且其精度优于基于特征的方法.基于灰度的相似性测度函数最常使用的是互信息或其变体,但互信息作为相似性测度函数应用于多模态医学图像配准中,有其自身难以克服的缺点：①它假设待配准的图像之间有相似灰度分布,但是对于差异很大的医学图像来说,这种假设不一定完全成立;②仅考虑了图像的灰度分布,完全忽视了图像的空间和几何信息;③互信息实现过程中需要计算灰度的联合分布,复杂度高,易导致优化过程陷入局部极值[2].

目前,针对这些缺点,在计算互信息的基础上提出了很多改进的新相似性测度函数[3- 8].Pluim等[3]提出将互信息与两待配准图像的局部梯度信息合成的项相乘获得测度GMI,它与MI相比提高了配准的鲁棒性;但它并不是MI的扩展测度,只是在MI计算式上增加了描述邻域信息的乘性因子.Russakoff等[4]对二阶互信息进行扩展,提出了区域互信息量(RMI),它在局部范围内计算两幅图像的互信息量,反映了局部图像的灰度分布,获得了比传统MI更好的鲁棒性结果;但它需要计算更高维概率分布的熵,增大了不确定性数据的统计.Loeckx等[5]提出了条件互信息方法(CMI),它将空间信息作为一个额外通道作用于联合概率分布的计算.空间信息取自于每一对应灰度对的指定区域间距离倒数;它改善了配准精度,但相应的解剖结构在空间上进一步被分开,使一些结构特征被忽略.Rivaz等[6]将自相似性质加权于互信息的计算过程,提出了自相似互信息的测度(SeSaMI),它充分利用了图像的局部特征结构来增强互信息的鲁棒性.Luan等[7]提出了定质定量的互信息方法(Q-MI),该方法增加一个效用系数到传统互信息计算;它的计算特别复杂而很难用于实际使用.Hossny等[8]提出了局部互信息(LMI)的配准方法,该方法将图像空间划分为多个子空间,每个子空间各自独立地估计互信息,再将各个子空间的互信息的加权和作为相似性测度;它不仅对待配准图像作了相关性统计,也包含了结构和梯度信息.

基于互信息改进理论的启发,结合空间与几何信息到互信息计算过程的设计思路,本研究提出了基于局部结构张量-互信息新测度的配准方法.局部结构张量[9- 12](LST)直接使用图像灰度矩阵进行运算从而可以很好地保存图像像素的结构信息,同时包含了每一像素点梯度的大小和方向,提供了比图像梯度信息更有意义的描述.文中从局部结构张量中提取的结构信息整合到互信息的计算中,获得了一个新测度函数(简称为LST-MI).局部结构张量的特征值的变化能够预示图像平坦区域、边缘区域或角点区域,能够很好地体现图像的显著性特征,且这些特征方便提取,具有实际应用意义.

1 基于LSI-MI的配准方法流程

文中所提出的新相似性函数LST-MI作为配准过程的相似性度量,将空间结构信息整合到互信息计算中，克服了互信息的缺点,有效提高了配准的鲁棒性.基于LST-MI配准的基本流程如图1所示.该流程的关键部分是相似性测度的选取和最优化策略.文中选取的是LST-MI的相似性测度,采用了最速下降优化方法做配准实验.插值方法的目的是根据已经获得的变换参数将像素灰度值重新采样到新的坐标系统.

2 LST-MI相似性测度

从局部结构张量中提取到的结构信息作为互信息的权重函数,该函数对处于突出几何结构位置的像素赋予大的贡献值,对平坦结构的像素赋予小的贡献值,获得结合了空间信息的新测度.该测度联合分布律的计算方式区别于MI测度,它将由局部结构张量提取的每一像素的局部结构描述子作为加权函数整合到联合分布律的计算,使得图像的空间信息得到有效利用.

图1 配准算法流程图Fig.1 Algorithm flowchart of registration

2.1 局部结构的权值函数描述

局部结构张量被广泛用于表示图像局部方向与各向异性程度的结构信息,允许同时进行方向估计和结构分析,有效避免了单一梯度信息对噪声敏感的缺点.它不仅能很好地区分图像的不同结构,而且能够度量像素点邻域内结构特征的各向异性.图像每一点的局部结构张量如式(1)所示：

LST(i,j)=Gσ*(I·I(i,j)T)=

(1)

对LST(i,j)进行奇异值分解,可以得到局部结构张量的非负特征值λ1,λ2(λ1≥λ2≥0),分别对应了特征向量v1、v2且v1⊥v2.λ1和λ2提供了这两个正交方向上的边缘强度或角点强度估计[13].为了度量每个像素点在图像几何结构中的贡献强度,文中由局部结构张量提取了如下局部结构描述子：

c=max(c1,c2)/b

(2)

其中,b是归一化因子.

空间每一位置上像素的边缘结构强度度量c1、角点结构强度度量c2和融合的结构强度度量c的三维图如图2所示.图中颜色越深代表权重值越大,像素处于平坦区域时c趋于0;当像素处在边缘或角点位置处时,c的值接近于1;故根据c的值可以自适应地区分图像的内容,c的值越大图像的结构强度越强.但c的取值范围在0～1之间，像素的权值之间比值可能无穷大或无穷小，若直接加权于互信息的计算过程,会导致偏离实际的结果值.文中选择w作为权值函数，如式(3)所示，将它结合于互信息的计算过程.函数w的取值在(1,2)之间,像素的权值之间比值介于(1/2,2)之间,它既可以区分图像结构强度信息,又确保平滑作用于互信息计算过程.

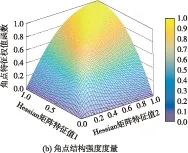
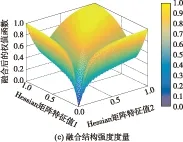
图2 权值分布三维图Fig.2 Three-dimension graph of weight distributing

w=1+c

(3)

为了验证c所表示的结构信息对多种模态均有很强的鲁棒性,文中对3种模态图像分别使用融合的结构强度度量c进行结构映射，映射的结果图像如图3所示.

图3 原始图像和提取的结构图像Fig.3 Original image and extracted structure images

由图3可见，3种不同模态都能够精确提取出结构信息,与理论分析一致.此外,考虑到λ1和λ2值的大小受高斯滤波方差σ取值的影响,文中通过对σ取多个不同的值,相应地可获得多组特征值,对所有的特征值取出最大值作为λ1(其中λ1≥λ2≥0)的值,取出最小值作为λ2的值.通过对σ多尺度的选值,进一步增大了对结构特征选择的区分度.

2.2 LST-MI新测度函数表达式

MI的计算是基于概率分布的,需先估计联合灰度直方图或由核函数得到的联合分布概率,但联合直方图的估计精度局限于填充直方图的有效采样个数和直方图所选bins的个数.为克服上述局限,文中选用非参数核密度估计法来计算两图像间的联合分布[15].非参数核密度估计法不受有效采样个数和直方图的bins数影响,也不需预先选择一个分布函数,减少了来自插值算法引起的量化误差,降低了对测试图像二进制化时的离散化程度.

核函数选择的是0次B样条和3次B样条函数.假设R和T分别表示参考图像和测试图像,fR(S)和fT(S)分别是两图像在位置S处的灰度值,κ和l分别是两图像的直方条的索引值,ΔbR和ΔbT分别是两图像直方图的组距.g(S;μ) 是测试图像域V上的S点映射到参考图像域的变换函数,那么联合概率分布函数可由式(4)计算得到[15].

(4)

x=(fR(S)-min (fR(S))/ΔbR

(5)

y=(fT(g(S;μ))-min (fT(g(S;μ)))/ΔbT

(6)

式中,β(0)、β(3)分别是0次和3次B样条函数,x和y分别为每一像素所在bin的位置,α是归一化常数.

LST-MI与MI计算方式的区别主要在联合分布概率密度的计算.从LST中提取的特征描述的结构映射函数w代表的是图像每一位置的结构强度.结构越明显,强度值越大,将它如式(7)的方式与联合分布概率密度函数相结合,然后将新联合分布概率密度用于LST-MI的计算,其对应测试图像和参考图像的边缘分布概率密度函数可分别由pw(l,μ)和pw(k)来表示.那么,提出的新测度函数LST-MI的表达式如式(8)所示.

(7)

(8)

2.3 配准模型的优化求解策略

2.3.1 优化方法

本研究将图像配准求解问题转化为代价函数的优化求解问题,主要思想是寻找最优的变换参数μ,使得代价函数达到最小值.配准问题的数学表达式如式(9)所示.

μ*=arg mingΦ(IR,IT∘g(μ))

(9)

其中,代价函数Φ是负的LST-MI测度函数，g是刚性变换函数，符号∘ 表示IT与函数g的复合运算.由于联合分布概率密度函数中引入的结构映射函数w的取值来自于参考图像,与变换参数μ无关,没有改变MI的B样条Parzen窗的特性,而且联合分布概率函数计算过程完全遵循了MI的计算方法,因而代价函数Φ可以看作关于μ(n个相互独立参数集)的函数.为了获得这个最优的参数μ,文中采用了最速梯度下降法迭代的更新参数值，如式(10)所示[16].

μk+1=μk-akΦ(μk)

(10)

其中，ak是搜索步长,Φ(μk)是代价函数的梯度,作为搜索方向.

该算法终止条件是梯度向量的幅值接近0,最终的输出参数是μ*.

2.3.2 代价函数梯度的计算

为了计算代价函数的梯度,首先给出了代价函数Φ的导数形式(如式(11)所示).代价函数的梯度是由μ的相互独立的元素组成的向量,如式(12)所示.

(11)

(12)

观察式(11)和(12)可知,最终要解决的是加权后的联合分布概率函数pw偏导的表达式.由于w与变换参数μ无关,因而pw关于μ的单一参数偏导的计算方法与传统的联合概率分布函数p相似如式(13)所示.

(13)

其中，|V|是像素总数,fT(t)是图像的空间梯度,g(x;μ)是关于μ的刚性变换函数(即也是由复合的初等函数组成).

由上可知,代价函数Φ的梯度是由如下基本函数所复合的解析式,包括3次B样条函数、梯度函数和刚性变换函数.因此，最终得到的新测度梯度是

一个解析表达式,它比基于直方图计算方法不仅应用了更多的信息，而且简化了计算复杂度.

3 实验结果分析

为了验证所提LST-MI度量作为相似性函数在配准过程中的鲁棒性和精确性,分别采用了Keith等[17]提供的全脑图谱(The Whole Brain Atlas)中的模拟脑图像和美国Vanderbilt大学图像配准评估项目[18](Retrospective Image Registration Evaluation)中同一病人的多模态临床脑图像进行试验.实验环境是：CPU Intel Xeon(R) X5690,主频3.47 GHz,内存192 GB,开发环境Matlab2013a.

3.1 LST-MI测度的有效性实验

为了验证新测度LST-MI度量两图像间相关度的有效性,文中选择了如图4所示的参考图像和测试图像的组合,对每个组合的测试图像分别做沿x轴均匀间隔的平移和绕图像中心点的旋转,将变换后的图像与参考图像依次使用LST-MI和MI测度进行相似性测量,绘制成如图5的曲线图.

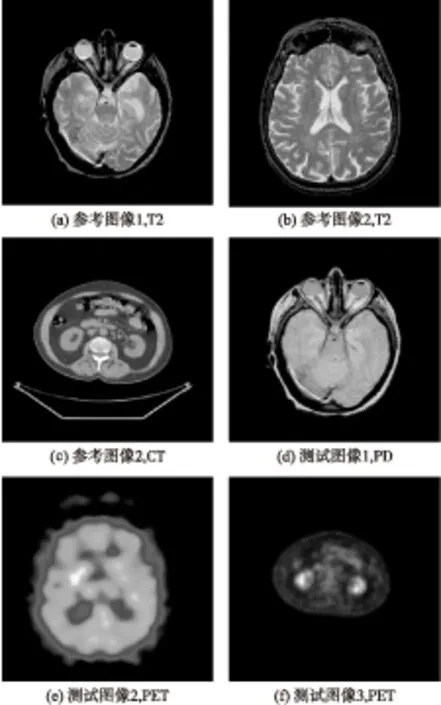
图4 不同模态的参考图和测试图Fig.4 Different modes of reference and test image

由图5可见,所有LST-MI曲线均能够得到比MI曲线更尖锐的峰、更少的局部极值点.此外,图5 (f) 中由于CT和PET仅仅有唯一的相似特征即脑图像的整体轮廓特征且平移变换会引起两图像重叠部分急剧减少的原因, MI曲线未能找到正确极值点.然而,LST-MI的曲线仍然能够找到正确的全局极大值点,因而所提新测度比MI具有更强的鲁棒性.基于所提新测度LST-MI的配准方法比基于MI配准方法能够更有效且更易成功地完成多模态的配准.

3.2 LST-MI算法鲁棒性、精度和速度评估

为了分析和验证 LST-MI作为配准代价函数的配准鲁棒性、精度和速度,文中分别使用MI、LMI和LST-MI做配准实验.所有实验均采用最速下降的优化方法,实验对象为文献[19- 20]中的模拟脑图集和临床病人的多模态脑图集.

3.2.1 模拟脑图集的配准结果分析

由表1可见,基于 LST-MI配准方法的两种组合成功率均高达90%以上,远远大于基于MI和LMI的配准方法,配准成功率平均提高了50%以上,配准鲁棒性显著增强.由于不同加权的MRI图像所突出不同组织的灰度统计具有局部特性,使得MI对待配准图像灰度全局一致的统计特性的假设不再成立,其成功率还不足50%,不适用于结构特征明显的多模态图像配准.LMI度量利用了空域信息,但没有考虑不同位置像素的效用信息,其鲁棒性虽强于MI度量,但仍然不是很理想.另外,表中W的均值n越小表明其配准精度越高,MI的n值略低于LST-MI和LMI的值,但实验中MI成功配准的图像对之间最佳的平移和旋转幅值范围均很小,确保了配准的较高精度,若最佳的平移和旋转幅值范围较大时，MI不能够成功配准,因而不具参考意义.最后,由于LST-MI将结构越强的位置赋予较大的度量值,减少了配准过程中陷入局部极值的风险,使得基于LST-MI配准方法的平均迭代次数高达50次左右,而基于LMI和基于MI的迭代次数仅4次左右.基于文中所提算法完成配准的平均时间约14 s,而基于LMI 和 MI 完成配准平均时间相近(约4 s).基于文中所提新测度的配准方法配准平均时间较基于LMI和MI的方法延迟约10 s,这主要是由于所提新测度增加了提取结构信息过程,加之配准优化过程迭代次数的增加共同导致了配准时间略有延长.

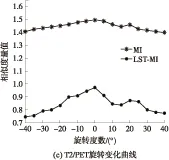
图5 相似度量值Fig.5 Similarity measure values

表1 模拟脑图集PD/T2和T1/T2配准结果分析

3.2.2 临床病人的多模态脑图集配准结果分析

为了进一步验证所提LST-MI的配准性能,文中采用了RIRE中的取自同一病人的PD/T2、T1/T2图像进行配准实验,其中MR图像的大小为256×256×25.实验中,从三维图像数据中取出来自同一病人两种不同模态(即PD/T2组合和T1/T2组合的多模态)各12组二维图像,图像大小均取为256×256.实验所采用的评价方法是配准后图像与参考图像之间的均方根误差(RMSE)、归一化互信息(NMI)和归一化互相关(NCC).为了衡量配准精度提高程度,文中采用文献[20]中所定义的精度提高程度P来衡量,计算公式如式(14)所示.

P=(RMSEe-RMSEp)/RMSEe×100%

(14)

取P1、P2分别为LMI、LST-MI相比于MI的配准精度提高程度.12组RIRE中patient 1的PD/T2和T1/T2模态图像组合的配准结果分析如表2所示.

由表2可见，LST-MI的RMSE值均最小,NCC和NMI的值均较大； 基于LST-MI的配准方法在PD/T2和T1/T2两种组合模态下的迭代次数均值、配准时间均值相比于基于MI和LMI的配准方法均有所增加，临床图像采用基于LST-MI配准方法造成的时间延迟原因与3.2.1节中模拟脑图集的配准原因相同；基于LST-MI方法的配准精度提高幅度大于基于LMI方法的提高幅度，另外,LMI算法受分块尺寸大小的限制,增加了计算代价.综上所述,所提方法的6种评价值均优于MI和LMI,这与前面模拟脑图像的实验一致,进一步验证了所提方法是一个更优的相似性测度.

表2 临床病人PD/T2和T1/T2配准结果分析Table 2 The analysis of registration result from clinical patients PD/T2 and T1/T2

4 讨论

所提方法应用于高维数据或临床实践时的高计算代价是其挑战性难题之一.为了加快该方法的计算速度,可以选择通过GPU实现该方法或使用并行计算的策略,也可以使用更先进的优化方法提高收敛速度如回溯线性搜索的梯度下降优化方法.

由于PET模态图像的灰度分辨率极低,结构特征不明显,所提取的每一位置像素的效用值区分度小,对配准结果改善程度不太明显,提出的方法更适用于具有明显结构特征的图像.

最后,本研究将局部结构张量特征值所形成的局部结构映射函数嵌入到MI的函数表达式中,这种权值方式可以推广到与其相似的局部结构映射函数，如SSIM作为每一像素位置处的效用值嵌入MI函数,获得更多的新相似性测度.

5 结论

针对MI测度完全忽略了空间结构信息的缺陷,文中提出了将结构张量产生的局部结构特征结合于MI的新测度,该方法有效地减少了局部极值的影响.不同模态组合实验表明,相比于MI和LMI方法，文中所提方法的配准成功率和鲁棒性都得到了较大改善；但对于分辨率低的模态图像配准实验(如PET模态图像),其配准精度和成功率仍然不太理想,有待于更进一步的研究.

[1] OLIVEIRA F P,TAVARES J M.Medical image registration：a review [J].Computer Methods in Biomechanics & Biomedical Engineering,2014,17(2):73- 93.

[2] WOO J,STONE M,PRINCE J L.Multimodal registration via mutual information incorporating geometric and spatial context [J].IEEE Transactions on Image Processing,2015,24(2):757- 769.

[3] PLUIM J P W,MAINTZ J,VIERGEVER M A.Image registration by maximization of combined mutual information and gradient information [J].IEEE Transactions on Medi-cal Imaging,2002,19(8):809- 814.

[4] RUSSAKOFF D B,TOMASI C,ROHLFING T,et al.Image similarity using mutual information of regions [M].Berlin：Springer-Verlag,2004:596- 607.

[5] LOECKX D,SLAGMOLEN P,MAES F,et al.Non-rigid image registration using conditional mutual information [J].IEEE Transactions on Medical Imaging,2010,29(1):725- 737.

[6] RIVAZ H,KARIMAGHALOO Z,COLLINS D L.Self-simi-larity weighted mutual information：A new nonrigid image registration metric [J].Medical Image Analysis,2014,18(2):343- 358.

[7] LUAN H,QI F,XUE Z,et al.Multimodality image registration by maximization of quantitative-qualitative measure of mutual information [J].Pattern Recognition,2008,41(1):285- 298.

[8] HOSSNY M,NAHAYANDI S,CREIGHTON D,et al.Image fusion performance metric based on mutual information and entropy driven quadtree decomposition [J].Electronics Letters,2010,46(18):1266- 1268.

[9] HE Z,XIN C,SUN L.Saliency mapping enhanced by structure tensor [J].Computational Intelligence & Neuroscience,2015,2015(4):1- 8.

[10] PRASATH V,VOROTNIKOV D,PELAPUR R,et al.Multiscale Tikhonov-total variation image restoration using spatially varying edge coherence exponent [J].IEEE Transactions on Image Processing,2015,24(12):5220- 5235.

[11] ESTELLERS V,SOATTO S,BRESSON X.Adaptive regularization with the structure tensor [J].IEEE Transactions on Image Processing，2015,24(6)：1777- 1790.

[12] 唐科威,刘日升,杜慧,等.一种基于张量和洛仑兹几何的降维方法[J].自动化学报,2011,37(9):1151- 1156.

TANG Ke-wei,LIU Ri-sheng,DU Hui,et al.A novel dimensionality reduction method based on tensor and Lorentzian geometry [J].Acta Automatica Sinica,2011,37(9):1151- 1156.

[13] KANAEV A V,HOU W,RESTAINO S R,et al.Restoration of images degraded by underwater turbulence using structure tensor oriented image quality (STOIQ) metric [J].Optics Express,2015,23(13)：17077- 17090.

[14] KOTHE U.Edge and junction detection with an improved structure tensor [C]∥Proceedings of Dagm Symposium.Magdeburg：Springer,2003:25- 32.

[15] PARK S B,RHEE F C,MONROE J,et al.Spatially weighted mutual information image registration for image guided radiation therapy [J].Medical Physics,2010,37：4590- 4601.

[16] KLEIN S,STARING M,PLUIM J P W.Evaluation of optimization methods for nonrigid medical image registration using mutual information and B-splines [J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2008,16(12):2879- 2890.

[17] KEITH A,JOHNSON M D.The whole brain atlas [EB/OL].(2013- 03- 06) [2016- 08- 15].http:∥www.med.harvard.edu/AANLIB/home.html.

[18] MICHAEL F J.Retrospective image registration evaluation project [EB/OL].(2010- 07- 08) [2016- 08- 15].http:∥www.insight-journal.org/rire/index.php.

[19] DEBAYLE J,PRESLES B.Rigid image registration by general adaptive neighborhood matching [J].Pattern Recognition,2016,55：45- 57.

[20] LIU X Z,YUAN Z M.Medical image registration by combing global and local information：a chain-type diffeomorphic demons algorithm [J].Physics in Medicine and Biology,2013,58(23)：8359- 8378.

Multi-ModalImageRegistrationontheBasisofLocalStructureTensor-MutualInformation

ZHANGLiLIBinTIANLian-fangLIXiang-Xia

(School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Mutual information (MI) measure considers the global characteristics of image gray statistics only, and ignores spatial structure information and local characteristics of image gray statistics. In order to overcome these drawbacks, a registration method on the basis of the new measure of local structure tensor-mutual information (LST-MI) is proposed. The proposed LST-MI measure considers the structure information of image neighborhood fully, gives the pixel position with greater importance larger weighting factor. Thus, the distinguishing of global extremum strengthens, the risk of trapping at local extremum reduces, the success rate improves, and the robustness of registration enhances. Moreover, some registration experiments are conducted on simulated brain images and clinical images. The results show that, in comparison with the registration method on the basis of mutual information and local mutual information, the proposed method improves the success rate of registration by more than 50%, and enhances the registration robustness significantly.

image registration; similarity measure;local structure tensor; mutual information

2016- 09- 18

国家自然科学基金资助项目(61305038, 61273249)；海洋公益性行业科研专项经费资助项目(201505002)；华南理工大学中央高校基本科研业务费专项资金重点资助项目(2015ZZ028)

*Foundationitems: Supported by the National Natural Science Foundation of China(61305038, 61273249)

张莉(1987-)，女，博士生，主要从事模式识别与医学图像处理研究.E-mail:88zhangli0622@163.com

†通信作者: 李彬(1979-)，男，副教授，主要从事医学图像处理与模式识别研究.E-mail: binlee@scut.edu.cn

1000- 565X(2017)07- 0098- 09

TN 391.41

10.3969/j.issn.1000-565X.2017.07.014