考虑换热能力和压降的永磁同步电机冷却流道设计*
万珍平 温万昱 吴柏禧 付永清
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.华南理工大学 设计学院, 广东 广州 510006)
考虑换热能力和压降的永磁同步电机冷却流道设计*
万珍平1温万昱1吴柏禧1付永清2
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.华南理工大学 设计学院, 广东 广州 510006)
现有的对电动汽车驱动电机水冷系统的研究主要集中在水冷系统的换热能力方面,对压力损失考虑不够.针对这一问题,文中首先以常用的驱动电机——永磁同步电机为对象,通过理论计算分析了流道结构参数对换热能力和压力损失的影响,发现流道螺旋圈数对换热和压力损失均有较大影响,而流道截面尺寸的变化对换热能力几乎没有影响,对压力损失影响较大,发现流道螺旋圈数对换热和压力损失均有较大影响,而流道截面尺寸的变化对换热能力几乎没有影响,对压力损失影响较大,提出了考虑换热能力和压力损失的流道设计方法,为高功率密度永磁同步电机水冷系统的设计提供了参考.
电动汽车;永磁同步电机;流道设计;换热能力;压力损失
为了缓解石油资源紧张和环境污染带来的问题,电动汽车的研发、生产受到了世界各国的广泛关注.驱动电机作为电动汽车的心脏,其性能好坏直接决定了电动汽车整车性能的优劣[1- 2].永磁同步电机具有低振动噪声、良好的转矩平稳性、高控制精度、高工作效率等优点,被普遍认为是最具竞争力的电动汽车驱动电机之一[3].但电动汽车要求驱动电机功率密度高、结构紧凑,导致电机单位体积损耗大,引起电机各部分的温升偏高.温升过高会破坏绝缘材料及稀土永磁材料的性能,影响电机安全稳定运行[4].
目前大多数永磁同步电机采用机座水冷的方式进行冷却,国内外学者对水冷电机温度场做了大量的研究.朱巍[5]利用有限元分析方法讨论了冷却水进出口水温、冷却水的流速、散热筋高度及机壳的水路形状对电机温度分布梯度的影响.乐智[6]利用Fluent进行了电机的温度场仿真,优化了流道.田玉冬等[7]建立了3种流道模型,提出一种流场均匀、冷却效率高的C型环槽水路结构.Jang等[8]利用CFD对使用冷却套管的开关磁阻电机的热场进行了分析并对冷却结构进行合理设计,提升了定子、转子以及端部绕组的冷却性能.沈启平等[9]利用Fluent研究了矩形截面流道尺寸以及流速对电机温升的影响.刘婉等[10]对电动汽车用电动机环形水套的冷却性能进行了研究,得到了不同电动机机壳流道的散热特性曲线和流动特性曲线.此外,国内外研究者对其他类型电机如外永磁转子横向磁通爪极电机、感应电机的水冷系统做了大量研究[11- 16].可见,目前对永磁同步电机和其他类型电机水冷冷却的研究工作主要集中在不同流道形状与截面形状对冷却性能的影响,只重视对流换热系数、温差、换热量等因素,而没有考虑流道的压力损失,结果易造成所设计的水冷机壳虽然冷却性能较好,但压力损失大,使配套的水泵因为扬程过大而体积变大,不利于电动汽车的轻量化.
本文以某公司生产的用于新能源汽车的MD23永磁同步电机为研究对象,从理论上分析不同流道参数对温升和压力损失的影响,得到较优的流道结构参数;然后利用仿真软件ANSYS Fluent对局部压力损失和整机温度场进行计算分析;最后总结出综合考虑换热性能和压力损失的电机水冷机壳螺旋流道设计方法和步骤.
1 流道几何参数选择
1.1 电机结构及流道参数
MD23永磁同步电机结构如图1所示,主要由水冷机壳、定子铁芯、定子线圈、转子、端盖、电机转轴等零部件组成.
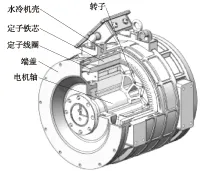
图1 MD23永磁同步电机结构示意图
Fig.1 Structure diagram of permanent magnet synchronous motor MD23
水冷机壳中流道结构如图2所示,流道形状为螺旋形,截面为矩形,出、入水口在机壳两端,旋向沿轴线方向.图2中,l为流道覆盖机壳的轴向宽度,D为流道螺旋直径,a为流道宽度,b表示流道高度.
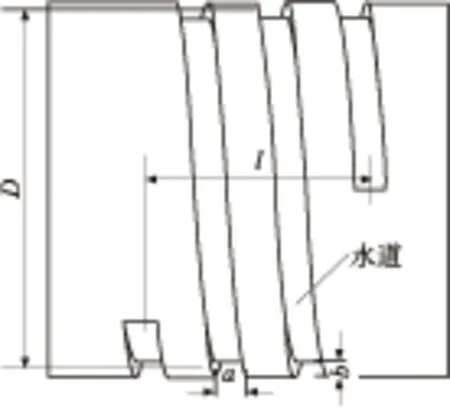
图2 水冷机壳流道参数示意图
电机相关的技术参数如表1所示,仿真与实验测试均采用电机在额定功率下的参数.

表1 电机相关技术参数
1.2 流道参数对冷却性能的影响
电机作为一种将电能转换为机械能的装置,在正常运转过程中,不可避免地会产生各种损耗,包括铁损耗、铜损耗、机械损耗、杂散损耗等,这些损耗绝大部分转换为热能.大部分热量通过定子铁芯与机壳的接触面传递给机壳,最终被机壳螺旋水道中的冷却水带走(如图1所示),极小部分通过空气自然对流作用带走.冷却水与流道表面的换热属于强制对流换热,满足牛顿冷却公式:
Φ=hAΔt
(1)
式中,Φ是总换热量,h是表面对流换热系数,A为换热面积,Δt表示流体与固体接触面的平均温差.
整个换热过程中没有发生液态水的物相转变,因此不考虑流体的物理性质对换热的影响,主要分析来自流动状态以及流道几何因素的影响.螺旋流道的截面为矩形,取其水力直径d作为流道特征尺寸进行计算:

(2)
式中,S表示水道截面积,C为水道湿周长度.
将体积流量换算为流速:

(3)
式中,Q为体积流量.
流道内流体的雷诺数为
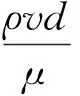
(4)
式中,Re为流体雷诺数,ρ为流体密度,v为流体速度,μ表示流体动力黏度.
上述公式中,各参数取值范围一般为:a=20~90 mm,b=8~12 mm,Q=15~30 L/min,计算出的雷诺数Re范围为104~7.5×104.管道内的流动可以分为层流与湍流两大类,通常以临界雷诺数Rec来衡量,其值为2 300.一般认为,Re>104的流动为旺盛湍流[17],2 300≤Re≤104为过渡区.因此文中研究的所有流动均属于旺盛湍流,对对流换热造成影响的则是流道的几何参数.利用相似原理,引入努赛尔数Nu:
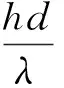
(5)
以及管槽内湍流强制对流传热关联式[17],即Dittus-Boelter公式:
Nu=0.023Re0.8Pr0.4
(6)
式中,λ为流体的导热系数,Pr为普朗特数.式(6)的适用范围为:Re=104~1.2×105,Pr=0.7~120,lp/d≥60.文中流体雷诺数Re=104~7.5×104,60 ℃水的Pr=2.99,lp/d≥60,均处于式(6)的适用范围.由于流道是螺旋形,流道内流体在向前运动的过程中会不断改变方向,即在截面方向上引起二次环流而强化换热,因此引入螺旋修正系数c[18]对努赛尔数Nu进行修正:
(7)
则式(5)修正为
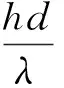
(8)
通常,由于电机安装空间有限,允许其外形尺寸变化的范围非常小.如何在有限的空间内合理布置螺旋水道以取得最优的换热效果和最低的压力损失是水道设计必须解决的难题.在物理模型成立的情况下,水道的总长度可以表示为

(9)
式中,n为水道螺旋圈数.总换热面积可表示为

(10)
联立式(1)-(9)得到平均温差Δt,可表示为

(11)
Δt表征固体接触面与流体平均温度的温差,它是关于流道几何参数a、b、l、D、n和体积流量Q以及总换热量Φ的函数.当总换热量Φ和体积流量Q一定时,可以用Δt来表征流道几何参数对对流换热能力的影响程度,Δt越大表示换热能力越差,造成电机的温升越高;Δt越小表示换热能力越好,电机温升越低.
1.3 流道参数对压力损失的影响
流体在流动过程中,由于流体的粘滞性和惯性以及固体壁面对流体的扰动和阻滞作用,会产生能量损失,造成流体压力损失.流体的能量损失分为两部分:沿程能量损失hf和局部能量损失hm[19].根据能量损失的叠加原理,整个水道的能量损失等于沿程损失和局部损失之和:
h1=∑hf+∑hm
(12)
1.3.1 沿程能量损失
沿程水头损失的计算由达西公式给出:

(13)
式中:λ1为沿程阻力系数;g为重力加速度.
Re=104~1.2×105范围属于紊流光滑区,λ1可以通过布拉修斯公式计算得到:
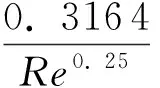
(14)
将水头损失换算成压力损失:
Pf=ρghf
(15)
上式也可以改写成:
Pf=f(a,b,Q,l,D,n)=
(16)
1.3.2 局部能量损失
局部水头损失的计算式为

(17)
式中,ζ为局部阻力系数.
虽然式(17)给出了局部水头损失的计算公式,但由于实际进出水口的形状非常不规则,很难通过理论或经验公式计算出局部阻力系数ζ的值,因此文中采用有限元法计算局部水头损失.
1.4 流道参数的选取
根据电机安装要求,确定电机MD23设计中的水道螺旋直径为418 mm,水道轴向覆盖宽度为190 mm,电机损耗为4 500 W.根据式(11)和式(16)可得到流道参数对温差和压力损失的综合影响,包括流道螺旋圈数n、截面宽度a和高度b对换热及压力损失的影响.当流道截面宽度为30 mm、高度为8 mm,体积流量Q为20 L/min时,螺旋圈数n对换热及压力损失的影响如图3所示.
从图3可以看出,当螺旋圈数增加时,平均温差呈现明显下降趋势,最终降低4℃左右.在流道截面形状不变的情况下,螺旋圈数的增加会增大换热面积,提高换热量,从而使平均温差下降;而随着螺旋圈数的增加,通道加长,造成流道压力损失迅速增加约11 kPa.可见,螺旋圈数对电机的温升和流道压力损失的影响非常大.根据图3,为保证流道具有足够的散热能力和较小的压力降,可选取流道的螺旋圈数为4.
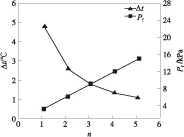
图3 螺旋圈数对换热及压力损失的影响
Fig.3 Influence of twist number on heat transfer and pre-ssure loss
一旦流道螺旋圈数确定,就可以确定流道宽度和高度.图4和图5分别给出了流道宽度和高度对平均温差Δt和压力损失的影响.
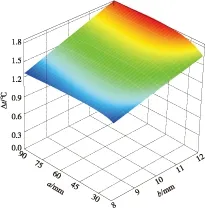
图4 流道宽、高对电机平均温差的影响
Fig.4 Influence of the channel width and height on mean temperature difference of the motor
从图4可以看出,当水道宽度增加时,平均温差几乎保持不变,表明水道宽度对对流换热几乎没有影响.这是因为随着宽度变大,通道内流速下降带来的换热弱化效果与换热面积加大带来的换热强化效果相互平衡;但由图5可看出,随着流道宽度的增加,流道的压力损失迅速下降.当流道高度为8 mm时,随着流道宽度的增加,压力损失下降约26 kPa.从图4还可看出,当流道高度增加时,平均温差缓慢增加,但变化量不超过0.5 ℃,表明水道高度对对流换热的影响较小;由图5可知,当流道宽度大于40 mm时,随着流道高度的增加,压力降几乎不变化,但当流道宽度小于30 mm时,随着流道高度的增加,流道的压力损失不断下降直至约9 kPa.
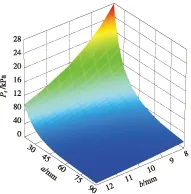
图5 流道宽、高对压力损失的影响
Fig.5 Influence of the channel width and height on pressure loss
由上述分析可知,流道宽度和高度对电机温升的影响较小,但对压力损失影响很大.因此,当流道螺旋圈数确定后,不用过多考虑散热,主要考虑流道的压力损失.设计时,由于出入水口的局部压力损失无法估计,因此应留有一定余量.根据生产实践经验,以7.5 kPa为流道沿程压力损失的限值,从图5中提取压力损失为7.5 kPa时,所有水道高度和水道宽度的组合,并将其所对应的平均温差值做成一条曲线,如图6所示.
从图6可以看到,此时的温差曲线呈现明显的单调性.随着流道尺寸的宽度变小、高度变高,平均温差保持微幅上升趋势,变化幅度不超过0.3 ℃.因此,图6所示的一系列的宽高组合构成了流道截面尺寸选择域,域中所有组合均满足电机冷却和压力损失的要求,设计时可根据具体机座、具体结构合理地选用流道尺寸.

图6 沿程压力损失为7.5 kPa时流道的平均温差曲线
Fig.6 Mean temperature difference curve of channels in the conditions of pressure loss of 7.5 kPa along the channels
2 整机温度场和压力损失的仿真计算
通过理论分析,确定了如图6所示的流道几何尺寸的选取范围,既保证了其具有较好的散热能力又具有较小的沿程阻力损失.但理论计算无法得到出入水口的局部损失,也无法了解整机的温度场分布情况,因此需要用有限元方法计算局部压力损失和整机温度场,以判断整机温度场和压力损失是否满足要求.
2.1 基本假设
所选用的永磁同步电机为外定子内转子结构.电机绕组由多股细小覆漆铜线绕制而成,各个方向的导热系数不同,建模困难,需要对绕组进行适当等效.考虑到这款永磁同步电机转子上的损耗非常小,且通过转子、电机轴、机壳、端盖与空气发生的自然对流交换的热量非常少,可以对模型进行适当简化.此外,为了提高计算分析效率,需做以下假设:
(1)绕组为一整体,具有各向异性导热系数;
(2)忽略电机转子、电机轴、端盖、轴承对电机传热的影响;
(3)冷却水为等速均匀地流入机壳流道;
(4)忽略热辐射.
2.2 有限元模型的建立
在流道截面尺寸选择域中选择流道尺寸为宽度30 mm,高度9.5 mm,并建立电机有限元模型如图7所示,基本网格尺寸为2 mm,大部分采用结构化网格,局部接触面网格细化,最终网格数为1.38×106,节点数为1.17×106.为避免网格尺寸过于粗大带来的计算误差,文中还对该模型进行了网格无关性检查,结果表明,将网格尺寸更改为1 mm后,其计算结果相差约0.72%,而网格数为3.22×106,增加了近两倍.因此,2 mm的网格足以满足运算需求并具有经济性.


图7 整机及流体有限元模型Fig.7 Finite element model of the motor and fluid
计算中使用的发热功率是根据电机的铜损和铁损分别赋予线圈和铁芯的体积源项.需要说明的是,电机的杂散损耗通过经验公式计算,作为了定子铁损的一部分.根据实际情况,绕组线圈和铁芯槽间还应放置槽间绝缘纸,由于其厚度只有0.35 mm,不宜直接建模,因此在Fluent中作为接触面接触条件设置.线圈采用外包绝缘的铜线绕制,其轴向和径向的导热系数有很大差异,须由实验测定.为测定线圈等效导热系数时,制作了截面尺寸为30 mm×10 mm、槽满率为75%的线圈样品,并通过保护热板法测定其径向导热系数.铁芯为表面涂有绝缘漆层的硅钢片叠压而成,其轴向与径向导热系数也有很大差异,亦须通过实验测定,测定所得的参数见表2.
文中流体流动为高雷诺数流动,因此采用了标准K-ε湍流模型[20].为了在减少计算量的基础上尽可能提高计算精度,在仿真中应用了壁面函数对近壁面的流动和换热情况进行处理.其中描述近壁面第一层网格的参数为Y+值,其与当地湍流速度、黏度有关.文中流体近壁面Y+平均值为61.2,处于对数层,可以很好地近似近壁面的流动和换热情况[21].
表2 有限元模型参数
Table 2 Parameters used in the finite element model

参数数值湍流模型标准K-ε壁面函数RNGK-ε流体网格Y+61.2是否进行网格无关性验证是铜损额定 4kW铁损额定 0.5kW工作制额定 S1连续工作制线圈导热系数轴向 387W/(m·K)径向 1.56W/(m·K)铁芯导热系数轴向 4.43W/(m·K)径向 39W/(m·K)绝缘纸导热系数0.18W/(m·K)绝缘纸厚度0.35mm
2.3 模型验证
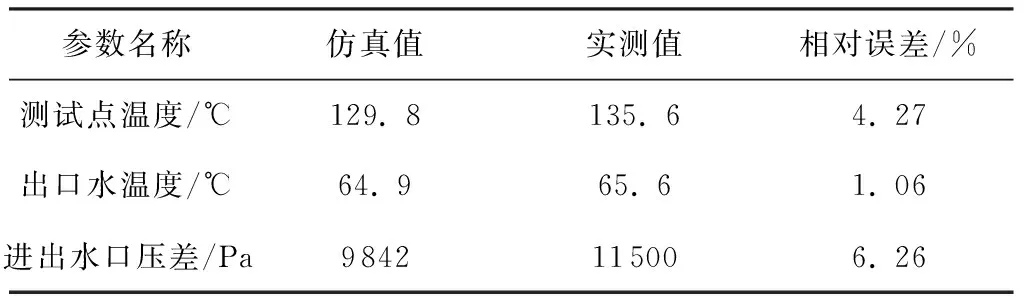
电机上某测试点的温度、出口水温以及压力损失的有限元计算值和实测值的对比如表3所示.实验在专业生产新能源汽车驱动电机的某公司实验室的电机特性试验台上进行,实验室环境温度31.6 ℃.
从表3可以看到,测试点的实际温度比仿真温度高约4.27%,出口水温的实测值也比仿真值略高.这是因为仿真时忽略了机械损耗和转子、磁钢等损耗的影响.虽然在这款电机中相比于定子损耗,这些损耗非常小,但不可避免会略微影响整机的温度场.从表3中还可看出,压力损失仿真值比实测值低6.26%,这是由两方面因素造成的:一方面,压力传感器的安装位置比仿真模型的进出水口略远,造成采集到的压差比实际流道的压差偏大;另一方面,在建模时为了减小计算机负担,删除了流道一些细小的转角特征而建立了一些圆滑过渡,这也造成计算出的压差比实际压差略小.
表3 仿真值与实测值对比
Table 3 Comparison between the simulation data and experimental date
参数名称仿真值实测值相对误差/%测试点温度/℃129.8135.64.27出口水温度/℃64.965.61.06进出水口压差/Pa9842115006.26
综上所述,仿真值与实测值的误差均在可接受范围内,能够满足一般工程要求,表明有限元模拟结果与实验结果吻合良好,验证了所建立的有限元模型的准确合理性.
3 有限元模拟结果分析
为了验证图6中流道截面尺寸选择域中的尺寸是否都满足设计要求,选定3组流道截面参数进行有限元分析,这3组参数分别取自选择域的两端和中部.3组参数下的流道压力损失情况如表4所示.可以看到,3组参数下的流道压力损失差异并不大,沿程压力损失与设计要求相吻合.
表4 三组流道截面参数下的压力损失
Table 4 Pressure loss in three sets of channel parameters

序号宽度/mm高度/mm沿程压损/Pa局部压损/Pa整体压损/Pa1388.077052425101302309.575552287984232511.07649249310142
3组参数下电机定子线圈温度分布、定子铁芯温度分布情况如图8、9所示.
从图8和图9可以看出,无论是线圈温度分布还是铁芯温度分布,均没有太大的变化,其最高温度差异均在1 ℃以内.证明选用流道截面尺寸选择域内的尺寸能够满足电机的设计要求,保证电机的温升及流道压力损失处于所设计的同一水平附近.
4 流道设计方法和步骤
根据上述研究,流道设计应在满足电机冷却要求的前提下,使流道压力损失尽可能小.具体设计方法和步骤如下:
(1)确定由于电机外形带来的不可变动或变动较小的尺寸,如文中流道的覆盖范围、流道的螺旋半径等;

图8 不同参数下电机定子线圈温度分布
Fig.8 Temperature profile of the stator coil of the motor under different parameters
(2)确定可以变动的流道尺寸范围,如流道宽度范围、流道高度范围、流道螺旋圈数范围;
(3)选定螺旋圈数,根据电机机壳冷却水流量的要求,得到流道宽度、高度与压力损失的关系图;
(4)根据电机机壳流道压力损失的最大值要求,通过保留一定余量,得到一个较小沿程压力损失上限值,并在流道宽度、高度与压力损失的关系图中提取所有满足该值的流道宽、高组合,组成流道截面尺寸选择域;
(5)将流道截面尺寸选择域中所有流道的宽、高组合与平均温差的对应关系绘制为曲线图,找到其中的最低点,提取其对应的流道宽、高组合.
(6)将得到的流道宽高组合代入机壳设计方案中进行工程可行性分析,如果工程上可行(如满足强度要求,模型没有干涉交叉等情况存在),则该流道宽高为最终尺寸,否则应在选择域中重新选择另一组尺寸;

图9 不同参数下电机定子铁芯温度分布
Fig.9 Temperature profile of the stator core under different parameters
(7)根据电机的相关安装尺寸对螺旋圈数进行调整,得到最终的电机流道参数.
5 结论
(1)流道螺旋圈数增加会造成电机温升显著下降,同时导致压力损失明显上升;流道截面尺寸的变化不会对电机温升造成明显影响,但随着流道特征尺寸的增加(不管是宽度还是高度变大),流道压力损失大幅降低.
(2)综合考虑换热性能和压力降,当流道螺旋圈数确定后,得到既满足电机冷却要求,又使压降较小的流道截面参数选择范围;有限元计算结果表明,在流道截面参数选择范围内选取的一系列宽、高参数,电机的温升和压力降均满足设计要求.
(3)提出永磁同步电机冷却流道的设计方法和步骤,为大功率电机的水冷机壳流道设计提供参考.
[1] CHAN C C,BOUSCAYROL A,CHEN K. Electric,hybrid,and fuel-cell vehicles:Architectures and modeling [J].IEEE Transactions on Vehicular Technology,2010;59:589- 598.
[2] WANG S W,ZHANG Y,HU J M.Thermal analysis of water-cooled permanent magnet synchronous motor for electric vehicles [J].Applied Mechanics & Materials,2014,610:129- 135.
[3] 赵立军,佟钦智.电动汽车结构与原理 [M].北京:北京大学出版社,2012:92- 109.
[4] 佟文明,程雪斌.高速水冷永磁电机冷却系统分析 [J].电机与控制应用,2016,43(3):16- 21.
TONG Wen-ming,CHENG Xue-bin.Cooling system analy-sis of high-speed water cooling permanent magnet motor [J].Electric Machines & Control Application,2016,43(3):16- 21.
[5] 朱巍.电动车用高功率密度永磁同步电机热管理系统的研究 [D].哈尔滨:哈尔滨工业大学,2010.
[6] 乐智.纯电动汽车电机驱动系的冷却系统设计与研究[D].天津:河北工业大学,2010.
[7] 田玉冬,王潇,张舟云,等.车用电机冷却系统热仿真及其优化 [J].机械设计与制造,2015(2):238- 242.
TIAN Yu-dong,WANG Xiao,ZHANG Zhou-yun,et al.Thermal simulation and optimization of cooling system for EVs’driving motors [J].Machinery Design and Manufacture,2015(2):238- 242.
[8] JANG J H,CHIU H C,YAN W M,et al.Numerical study on electromagnetics and thermal cooling of a switched reluctance motor [J].Case Studies in Thermal Engineering,2015(6):16- 27.
[9] 沈启平,韩雪岩.车用水冷高功率密度永磁同步电机的流体场分析 [J].微电机,2014,47(12):1- 5.
SHEN Qi-ping,HAN Xue-yan.Fluid field analysis of water cooling high power density permanent magnet synchronous machine for electric vehicles [J].Micromotors,2014,47(12):1- 5.
[10] 刘婉,邹海荣,唐守杰,等.电动机环形水道冷却性能及流动特性分析 [J].上海电机学院学报,2015,18(4):227- 231.
LIU Wan,ZOU Hai-rong,TANG Shou-jie,et al.Analysis of cooling performance and flow characteristics of motor annular water jacket [J].Journal of Shanghai Dianji University,2015,18(4):227- 231.
[11] LI Cui-ping,PEI Yu-long,NI Rong-gang,et al.Analysis of 3D static temperature field of water cooling induction motor in mini electric vehicle [C]∥International Conference on Electrical Machines and Systems.Beijing:IEEE,2011:1- 5.
[12] DARABI A,SARRESHTEHDARI A,TAHANIAN H.Design of the forced water cooling system for a claw pole transverse flux permanent magnet synchronous motor [C]∥Electrical Engineering.Mashhad:IEEE,2013:1- 5.
[13] LEE K-H,CHA H-R,KIM Y-B.Development of an interior permanent magnet motor through rotor cooling for electric vehicles [J].Applied Thermal Engineering,2016,95:348- 356.
[14] SONG Li-wei,LI Zi-jian,GAO Jing-yi,et al.3D thermal analysis of water cooling induction motor used for HEV [C]∥International Conference on Electrical Machines and Systems.Wuhan:IEEE,2008:534- 537.
[15] WANG Yu,HE Hui-ming,WANG Jia-yin,et al.Research of novel water cooling jacket for explosion-proof motor [C]∥International Conference on Electrical Machines and Systems.Busan:IEEE,2013:691- 694.
[16] ZHANG Xue-li,WANG Hai-feng,ZHANG Guo-qiang,et al.Temperature characteristics in the stator model of a permanent magnet motor by water-cooling and evaporative cooling [C]∥Proceedings of the Eighth International Conference on Electrical Machines and Systems.Nanjing:IEEE,2006:2408- 2410.
[17] 杨世铭,陶文铨.传热学 [M].北京:高等教育出版社,2006:198- 246.
[18] SHAH R K,JOSHI S D.Handbook of single-phase convective heat transfer [M].New York:Wiley-Interscience,1987.
[19] 刘建军,章宝华.流体力学 [M].北京:北京大学出版社,2006.
[20] 熊莉芳,林源,李世武.K-ε湍流模型及其在Fluent软件中的应用 [J].工业加热,2007,36(4):13- 15.
XIONG Li-fang,LIN Yuan,LI Shi-wu.K-εturbulent model and its application to the Fluent [J].Industrial Heating,2007,36(4):13- 15.
[21] 张涛,朱晓军,彭飞,等.近壁面处理对湍流数值计算的影响分析 [J].海军工程大学学报,2013(6):104- 108.
ZHANG Tao,ZHU Xiao-jun,PENG Fei,et al.Analysis of effect of near-wall treatments on numerical computation of turbulent flow [J].Journal of Naval University of Engineering,2013(6):104- 108.
CoolingChannelDesignofPermanentMagneticSynchronousMotorConsideringHeatExchangeandPressureLoss
WANZhen-ping1WENWan-yu1WUBo-xi1FUYong-qing2
(1. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China 2. School of Design, South China University of Technology, Guangzhou 510640, Guangdong, China)
As the existing researches on the water cooling system of motors applied to electric vehicles mainly focus on the heat exchange performance without taking full consideration into pressure loss, the influences of cooling channel parameters on heat exchange performance and pressure loss are analyzed theoretically for the frequently-used driving motor-permanent magnetic synchronous motor (PMSM), finding that the twist number of cooling channels influences heat exchange and pressure loss greatly, and that the transverse dimensions of cooling channel have little influence on heat transfer but have great influence on pressure loss. Thus, an optimal range of cooling channel parameters is obtained, with its validity being verified by simulating PMSM temperature field and pressure loss of cooling channels with optimized parameters through a finite element analysis. Finally, a new design method of cooling channels considering both heat exchange and pressure loss is presented. The research provides a reference for the design of water cooling system of PMSM with high power density.
electric vehicle; permanent magnetic synchronous motor; channel design; heat exchange perfor-mance; pressure loss
2016- 11- 02
国家自然科学基金资助项目(51275174);广东省科技计划项目(2014B010126003)
*Foundationitems: Supported by the National Natural Science Foundation of China(51275174)and the Science and Technology Planning Project of Guangdong Province(2014B010126003)
万珍平(1971-),男,博士,教授,主要从事现代加工理论及表面质量控制、表面功能结构先进制造及其作用机理等研究. E-mail:zhpwan@scut.edu.cn
1000- 565X(2017)07- 0025- 08
TM 301.4+1
10.3969/j.issn.1000-565X.2017.07.004

