架空导线径向温差对弧垂计算的影响*

刘刚 李炀 陈垣 杨宇航

(华南理工大学 电力学院， 广东 广州 510640)

架空导线径向温差对弧垂计算的影响*

刘刚 李炀 陈垣 杨宇航

(华南理工大学 电力学院， 广东 广州 510640)

建立了钢芯铝绞线径向温度场分布热路模型，利用有限元分析软件对不同载流值下导线截面的温度场进行计算，并分析了径向温差产生的原因，同时设计钢芯层和表层温度分布式实验进行验证.以实验结果为依据，讨论了不同的温差造成的弧垂计算误差，以及不同档距时的弧垂计算误差.研究结果表明：架空线径向温差随着载流量的提高呈增大趋势，自然对流情况下，表面温度70 ℃时，钢芯温度达到73.5 ℃，导致弧垂的计算误差逐渐扩大；在钢芯层和表层温差一定时，档距越大，计算误差越大，而相对误差越小.

架空导线；径向温差；有限元分析；弧垂

提高现有线路输送能力的主流技术包括静态增容技术和动态增容技术.静态增容技术即环境参数按照设计标准，提高导线运行温度到80 ℃,从而提高约20%的输送载流量；动态增容技术，即通过在线路上安装监测设备,实时监测导线状态、风速、日照强度和环境温度等环境参数，计算当前条件下的载流量[1- 5]，从而在不改变现行技术规程规定的前提下，提高线路载流量.无论是动态增容还是静态增容，随着导线的运行温度提高，弧垂势必要增加.《电力工程高压送电线路设计手册》规定弧垂定位温度是40 ℃或者覆冰无风条件[6]，当导线增容温度达到70 ℃或者更高时，对地距离或者交叉跨越距离很可能不满足规程，容易造成对地放电、树竹放电、电磁信号干扰或线路跳闸等危害[7- 8].

导线增容主要受配套金具发热、机械强度变化和安全距离限制等约束[9- 10].关于导线的张力-温度模型，一般是代入表面温度求解，在高温段时，模型误差偏大[11- 12].文献[13- 14]对导线径向热场分布的研究表明，由于各层单导线空气间隙的存在，架空导线钢芯与最外层铝绞线存在温度梯度.文献[15]对导线径向应力分布随时间的变化进行了研究，结果表明，随着温度升高，导线的应力向钢芯处转移.对于钢芯铝绞线，通常在40～110 ℃的时候，架空导线会变得松弛，在某个温度时，架空线的拉力全部由钢芯承担[15- 17].这种状态下，仅以表面温度为依据计算弧垂会造成误差.研究导线径向温差对弧垂计算造成的影响，应分析各种条件下架空线径向温度梯度的变化规律，以此为依据，研究线路参数、设计参数造成的误差，并以实验检验其有效性.由于导线实际结构复杂，之前所建立的解析模型需要考虑较多因素，计算量大，不适合工程应用.若能采用场的数值分析方法求取导线径向温差，则可直观了解导线径向结构温度分布[18]，同时为架空线三维弧垂模型的建立带来便利.本研究结合LGJ240/30 mm2型导线的规格尺寸，建立径向切面的二维有限元模型，通过求取钢芯温度和表面温度，分析了导线径向温差对导线弧垂计算的影响；通过大电流实验，得到钢芯铝绞线型导线表层温度和钢芯层温差随电流变化的规律，并对该有限元建模方法的有效性进行了验证.

1 导线径向热场解析分析

1.1 导线径向热路模型

架空输电线路大多采用钢芯铝绞线型(ACSR)，由多股铝线和钢线组成，各层导线和同层各股导线接触面并非平整，存在空气间隙[13- 17].钢芯铝绞线截面如图1所示.

图1 钢芯铝绞线截面

热路模型基于热电类比理论，将电路中的欧姆定律和节点电压法应用到热传导分析中，可以简化热场的分析[19- 21].

本研究根据图1所示的钢芯铝绞线的实际截面结构，建立径向结构二维热路模型，如图2所示.图中，n是钢芯铝绞线的导体层数；T1、T2、T3、Tn是钢芯和铝层各层温度监测点温度，Th是环境温度；Rc1、Rc2、Rc3、Rcn是钢芯层和铝层各层导体本身热阻，Ra1、Ra2、Ra3是各层导体之间空气间隙的接触热阻，Rh是外部环境的热阻.Q1、Q2、Q3、Qn是钢芯层和铝层各层导体产生的热量，单位W/m2；Qh包括钢芯铝绞线吸收的太阳辐射量Qs、对流散热量Qc和以电磁波形式向外辐射的能量Qr，单位W/m2.

标准大气压下空气导热系数为2.04 W/(m·K)，钢芯铝绞线各组成材料(铝线、镀锌钢丝)的导热系数为169、43.2 W/(m·K).由此可知，20 ℃时空气的导热系数分别是铝线和镀锌钢丝的1.2%、4.7%，所以在计算和分析各层温度时可以忽略各层导线本身的热阻Rci[21].由热路原理可得：

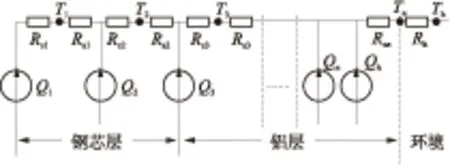
图2 钢芯铝绞线径向热场温度分布稳态热路模型

Fig.2 Steady thermal circuit model for radial temperature distribution of ACSR

(1)

考虑集肤效应和邻近效应，由于气隙和单导线氧化膜的存在，钢芯铝绞线结构中电流密度分布和圆柱型导体的差异很大，各层导线电流产生的热量通过导线之间的点接触和空气的热传导传递，空气热阻较大，温度主要降落在气隙中；此外，在运行中，导线温度不同、张力不同，接触面之间的空气隙结构也会发生变化，因而难以计算其热容和热阻.

1.2 钢芯铝绞线径向温度场有限元仿真

为了分析不同载流条件下钢芯铝绞线径向温度的差异，文中采用LGJ240/30型钢芯铝绞线实际结构尺寸，利用有限元分析软件建立导线截切面二维结构模型，并进行温度场的仿真分析.

(1)发热源计算

在施加发热源时，根据钢芯铝绞线的结构特点，钢芯热源由流过其电阻的电流产生，铝层热源包括焦耳热和吸收的太阳辐射.由于铝导体集肤效应深度远大于导线截面，假设流过各层导体之间、各股导体之间的电流值按照电阻串并联关系计算求得，钢芯铝绞线内部各导体之间的分流规律如图3所示.图中I为流过导体截面的总电流；Is为流过铝层导体的总电流；Isu为流过各股铝导体的电流；Ia为流过刚芯导体的总电流；Iav为流过各股钢导体的电流.

qsu、qav分别为单位长度每股钢导体和铝导体通电后的产热率(W/m2)， 按下式计算：

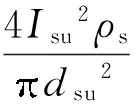
(2)

(3)

式中：dsu、dav分别为每股钢导体和铝导体的直径，m;ρs、ρa分别为20 ℃时钢线和铝线材料的电阻率，Ω·m；rs、ra分别为钢线和铝线材料的电阻温度系数，1/℃；Ts、Ta分别是钢线和铝线的运行温度，℃；β是导线的吸热系数，通常认为光亮新线的β为0.23～0.46，发黑旧线是0.9～0.95；Et是太阳辐射强度值，W/m2.

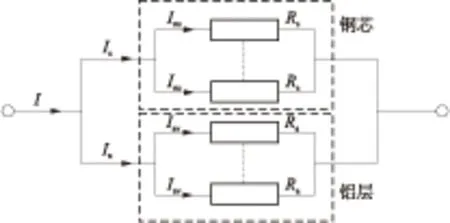
图3 钢芯铝绞线内部结构并联电阻图

(2)边界条件的施加

施加边界条件时，空气外边缘施加开放边界条件，热辐射边界条件[22- 23]为

(4)

绞线型导线表面结构较为复杂，难以准确确定表面综合散热系数，所以施加第三类边界条件.考虑到物性参数的温度相关性和流体场的求解，以导线轴心为圆心，建立半径为0.5 m的圆形空气域，环境温度设为24 ℃.自然对流情况下电流值为550 A时各层温度分布的仿真结果如图4所示.

由仿真结果的颜色区间可以看出，在自然对流、无日照条件下，导线各层温度分布存在明显梯度，钢芯层温度明显高于表面温度.根据复合散热量和温差的关系，导线表层与环境的温差比导线内外结构温差大，对流散热和辐射散热量较多，造成钢芯温度最高.此外，导线在无风情况下，导体产生的焦耳热加热周围空气，热空气上升冷空气下沉形成气体运动，通过计算，当温差40 ℃时，气流运动相当0.2 m/s的风速，致使导线表面温度分布不均，造成上表面的温度高于下表面的温度；由于导线最外层导体与空气接触，散热条件比内部导体好，所以该层导体温度梯度明显.由此可知，在输电线路巡视中使用的远程红外测温装置和在线监测中的接触式测温并不能有效地得到导体运行中的最高温度，从而为增容后电力运行带来灾害.

图4 自然对流情况下电流值为550 A时各层温度分布

Fig.4 Radial temperature distribution under natural convection when currrent is 550 A

2 实验设计与结果分析

2.1 实验平台设计

为进一步验证架空导线径向温差随加载电流的变化规律以及模型的有效性，搭建了大电流实验平台，如图5所示.

图5 实验平台示意图

实验装置主要由调压器、补偿电容器、升流器、LGJ- 240/30 mm2型实验导线、测温仪和小型气象站6部分组成.导线温度监测采用铜-康铜T型热电偶丝，测量精度为±0.5 ℃，采集周期为1 s，其在钢芯铝绞线各部位的测温点位置如图6所示.实验电流通过升流器耦合到导线上，调节调压器接头的位置，即可改变加载到导线上的实验电流值.小型气象站安置在温度监测点附近0.4 m处，以便实时监测周围温度、风速和湿度[24].

图6 钢芯铝绞线断面测温点布置图

Fig.6 Scheme of thermocouples layout on cross section over ACSR

2.2 实验结果分析

导线径向温差同时受到负载电流、日照强度、风速和环境温度的影响.结合现有实验条件，为保证实验的严谨性，仅考虑自然对流情况.实验在封闭室内进行，可视为无风条件，使用恒温器控制温度在23.8～25.8 ℃之间.实验过程中，通过在线设置，改变调压器分接头，使耦合到导线上的电流分别为250、350、450、550 A，每一电流强度下分别加载70 min，确保导线温度达到稳态[25].系统稳定时读取各点处测温仪的数据并绘制成曲线,如图7所示.

图7 架空线钢芯温度和表层温度实验曲线

Fig.7 Experimental results of steel core and surface temperature in ACSR

由图7可见：每一电流强度下加载70 min时，导体各位置温度可视为已达到稳定状态.在电流为250 A时，表面温度最低为38.6 ℃，钢芯最高温度为39.5 ℃，径向温差为0.9 ℃；而当电流为550 A时，钢芯最高温度为84.7 ℃，表面最低温度为80.5 ℃，温度差异达4.2 ℃.在导体各层温度达到稳态的过程中，钢芯铝绞线的钢芯温度高于铝线表层温度，随着加载时间的增加和加载电流的增大，这种差异逐渐明显.钢芯层由于受到铝绞线的包裹，产生的热量除了使本身的温度升高外，还向铝线传递，散热条件差；铝线层表面存在对流散热、辐射散热，因与环境温差较大，热阻小，散热条件好，因而表面温度较钢芯温度低.实验结果表明，以导线表面温度作为整个导体的温度，当测得表面稳态温度为80.5 ℃时，径向温差为4.2 ℃，并且在强迫对流或者导线松弛时，温差会进一步扩大[13].文中是以LGJ240/30 mm2为例，铝层和钢芯共计4层，对于大截面导线，层数增加，空气间隙增加，等效的空气层厚度会加大，导线的径向温度差异会更严重.因此，将表面温度代入温度-张力模型或者状态方程计算弧垂，显然是不合理的.

为验证有限元模型的正确性，在加载电流分别为250、350、450、550 A的条件下，按照实际的实验条件设置有限元模型的边界条件，计算钢芯和表层的温度，并与实验温度进行比较，结果如表2 所示.

CFG桩复合地基由于其承载力高、地基变形小、工程造价低等优良特性。目前，在高层和超高层建筑中得到广泛应用。但在CFG桩复合地基的设计中，由于对基本概念不清楚，有些设计人员提供给做复合地基设计的岩土工程师的资料不全面，给设计带来很多困难；或在设计过程中对一些参数的取值范围不明确，造成设计失误。给工程造成损失。为此本文就CFG桩复合地基设计中常见问题进行分析和探讨，以规范设计，提高其安全性和合理性。

表2 实验温度和计算温度的对比

Table 2 Comparison between experimental temperature and calculations

电流/A实验温度/℃钢芯表层计算温度/℃钢芯表层相对误差/%钢芯表层25039.838.640.039.70.52.935050.648.651.450.21.33.445066.663.564.962.8-2.7-1.055084.880.686.982.42.4-2.3

由表2可见，在导体温度低于50 ℃时，钢芯层仿真计算误差在2%以内；而在温度较高时，由于各层绞线存在的空气间隙随温度的改变发生微小变化，使得钢芯层温度的计算误差偏大，相对误差在3%以内.由上述导体各部位实验温度与仿真结果温度比较可知，相对误差小于工程要求的5%，所以自然对流条件下，该模型是有效的.

3 径向温差对弧垂计算误差的影响

当环境温度、风速、太阳辐射强度和负荷等参数改变后，架空导线温度会发生变化，导线产生热胀冷缩，相对于制造温度t0和原始长度L0，伸缩量L1为

L1=α(t-t0)L0

(5)

式中,α为导线膨胀系数，10-6/℃.

考虑外界条件造成的比载变化，导致轴向应力分布的改变，由应力-应变之间的关系，导线的长度进一步发生变化.假设钢芯铝绞线拉伸时处于弹性变形阶段，弹性系数E保持不变.根据胡克定律，可计算出导线由于弹性变形导致的线长伸缩量L2，如式(6)所示:

(6)

式中，σcp为导线的平均张力，MPa.

导线长度的总变化为

(7)

不同的导线温度、不同的风速和覆冰厚度造成的比载差值导致导线的伸缩量不同，在档内原始线长L0保持不变的情况下，各个状态的线长、平均应力等参数之间存在一定的关系.架空线的状态方程式就是揭示这种参数关系的方程，利用状态方程式可以由一种导线温度下的应力求出另一温度下的应力值[26]，进而利用弧垂和应力的函数关系求得此时的弧垂值.

工程中最常用的架空线状态方程式是斜抛物线状态方程式(架空线斜抛物线状态方程式详细推导过程参考文献[26])，不等高悬点架空线的斜抛物线示意图如图8所示.即使对于重要跨越档和高差很大的档距也能满足精度要求[26]，因此文中以斜抛物线状态方程式为依据讨论径向温差造成的弧垂计算误差，该方程式如式(8)所示.为方便描述问题，作如下基本假设：

(1)架空线为完全弹性体，不考虑长期运行产生的沉降应变和蠕变应变，认为弹性系数E和膨胀系数α保持不变；

(2)架空线为理想柔线，只承受拉力而不承受弯矩；

(3)架空线比载γ沿斜档距均匀分布.

αEcosθ(t2-t1)

(8)

式中：δ01、δ02是两种状态下架空线端点应力水平分量；γ01、γ02为两种状态下架空线比载，MPa/m；t1、t2为两种状态下的导线温度，℃

图8 不等高悬点架空线的斜抛物线示意图

Fig.8 Oblique parabola used in unequal suspension point of overhead lines

文中根据架空线的状态方程，以LGJ 630/45 mm2、LGJ 300/40 mm2、LGJ 240/55 mm23种型号的钢芯铝绞线为例，在高差为0、导线初始应力为25%的抗拉强度、初始温度为0 ℃的条件下，讨论档距500 m、表层温度为70 ℃，钢芯温度分别为72、74、76、78、80 ℃时造成的弧垂计算差异，具体计算δ02时，t02采用钢芯温度，计算结果如图9所示.

图9 不同径向温差造成的弧垂计算误差

Fig.9 Calculation error of sag casued by radial temperature differernce

在高差为0、导线初始应力为25%的抗拉强度、初始温度为0 ℃、表层温度为70 ℃、钢芯温度为80 ℃的条件下，档距分别为200、400、600、800 m时的弧垂计算差异如图10所示.

由图9可见，随着钢芯铝绞线钢芯层和表层温度的差异增加，计算所得弧垂误差逐渐增大，呈线性增长关系；当径向温差达到10 ℃时，LGJ 630/45 mm2、LGJ 300/40 mm2、LGJ 300/40 mm2的弧垂差异分别可达0.54、0.51、0.47 m.

由图10可见，随着档距的增加，弧垂的绝对误差随之增加，而相对误差在减小.在钢芯和表面温差为10 ℃时，档距200 m的弧垂计算差值是0.27 m，相对误差为9.1%；在档距800 m时，弧垂计算误差为0.64 m,相对误差为2.3%.

图10 不同档距下温差10 ℃时弧垂计算误差

Fig.10 Calculation error of sag casued by radial temperature differernce of 10 ℃ at different span

我国线路规程规定，按照经济电流密度设计的线路，正常容量运行时，导线温度一般约为29～42.3 ℃，即使在事故输送量下，线路重载运行时，导线温度可能达到最高允许运行温度，但时间较短，仅为20～30 min，弧垂变化不足以导致放电事故发生，所以对于一般线路，按照最高气温40 ℃计算的弧垂校验最小垂直距离，对于重要的交叉跨越(如一级公路)，则按照导线最高允许运行温度70 ℃校验交跨限距[27].以220 kV电压等级、档距500 m、导线型号LGJ 300/40 mm2为例，跨越非居民区的最小对地限距是6.5 m，并考虑线路设计杆塔定位时预留的限距裕度1 m.假设折算到40 ℃的最小对地距离满足规程规定的限距7.5 m，折算至70 ℃时，最大弧垂下降1.7 m，已突破规程规定；此时，如果按钢芯温度比外表层温度高10 ℃，即按照80 ℃校验限距，最大弧垂下降2.2 m，对地距离仅为5.3 m，很大程度上不满足规程要求.

依照上述计算结果，当线路负荷抬升或者长期高温运行时，由于对弧垂状态评估失准，对输电走廊微地形变化不能及时掌握，很容易出现对地距离、交叉跨越距离不满足规程规定的现象，出现分裂导线的粘连、绞扭和树竹放电甚至线路跳闸等危害.

4 结论

由于钢芯铝绞线各层绞线之间点接触并且存在空气间隙，以及表层散热条件较好，造成在载流情况下，径向方向存在温度梯度.在使用表面温度计算温度弧垂时，会出现较大偏差.文中通过建立钢芯铝绞线有限元计算模型，以及搭建实验测温平台进行模型验证，得出以下主要结论：

(1)仿真和实验结果表明，在自然对流以及不考虑太阳辐射条件下，采用本文建立的有限元计算模型是有效的，可得到架空线径向温差随着负载电流的变化趋势.

(2)结合架空线径向热场的实验和仿真结果，依据架空线的状态方程式，在档距一定时，随着径向温差的增大,所计算的弧垂误差逐渐扩大；在钢芯层和表层温差一定时，随着档距的增加，计算误差逐渐增大，而相对误差逐渐减小，在导线增容时，极有可能造成危害.

[1] 黄新波，孙钦东，张冠军，等．输电线路实时增容技术的理论计算与应用研究 [J]．高电压技术，2008，34(6)：1138- 1144．

HUANG Xin-bo,SUN Qin-dong,ZHANG Guan-jun,et al. Theoretical calculaton and application study on real-time capacity-increase of transmission lines [J].High Voltage Engineering,2008,34(6):1138- 1144.

[2] 徐青松，季洪献，侯炜，等．监测导线温度实现输电线路增容新技术 [J]．电网技术，2006，30：171- 176．

XU Qing-song,JI Hong-xian,HOU Wei,et al. The novel technique of transmission line’s capacity increase by means of monitoring conductor’s temperature [J]. Power System Technology,2006,30:171- 176.

[3] 王红斌，陈扬，高雅，等．输电线路弧垂对动态增容的影响 [J]．华北电力大学学报，2014，41(2)：41- 46．

WANG Hong-bin,CHEN Yang,GAO Ya,et al. Impacts of transmission line sag on dynamic capacity increase [J]. Journal of North China Electric Power University,2014,41(2):41- 46.

[4] 张辉，韩学山，王艳玲．架空线输电线路运行载流量分析 [J]．电网技术，2008，32(14)：31- 36．

ZHANG Hui,HAN Xue-shan,WANG Yan-ling. Analysis on current carrying capacity of overhead lines [J]. Power System Technology,2008,32(14):31- 36.

[5] 刘刚，阮班义，林杰，等．架空导线动态增容的热路法稳态模型 [J]，高电压技术，2013，39(5)：1107- 1113．

LIU Gang,RUAN Ban-yi,LIN Jie,et al.Steady-state model of thermal circuit method for dynamic rating of overhead lines [J]. High Voltage Engineering,2013,39(5):1107- 1113.

[6] GB 5045—2010 ，110～ 750 kV 架空输电线路设计规范 [S]．

[7] 郭振宇，张林波，刘宗川．220 kV输电线路风偏事故及防风偏改造 [J]．山西电力，2015(3)：37- 41．

GUO Zhen-yu,ZHANG Lin-bo,LIU Zong-chuan. 220 kV transmission line windage yaw fault and windage proof renovation program [J]. Shanxi Electric Power,2015(3):37- 41.

[8] 包建强，张勇，吴依群．220 kV架空输电线路相双分裂垂直排列导线粘连原因分析及技术防范措施 [J]．电气设备，2008，9(5)：76- 78．

BAO Jian-qiang,ZHANG Yong,WU Yi-qun.Case study and technical countermeasures of conductor adhesion with phase twin bundled and vertical arrangement for 220 kV overhead transmission line [J]. Electrical Equipment,2008,9(5):76- 78.

[9] MORGAN V T. Effect of elevated temperature operation onthe tensile strength of overhead conductors [J]. IEEE Transactons on Power Delivery,1996,11(1):345- 353.

[10] 叶鸿声．提高导线允许运行温度的可行性研究和工程实施 [J]．电力建设，2004，25(9)：1- 8．

YE Hong-sheng. Feasibility study on increasing conductor allowable temperature and engineering practice [J]. Electric Power Construction,2004,25(9):1- 8.

[11] 任丽佳．基于导线张力的动态提高输电线路输送容量技术 [D]．上海：上海交通大学，2008．

[12] SEPPA T O. Accurate ampacity determation:temperature-sag model for operational real time ratings [J]. IEEE Trasactions on Power Delivery,1995,10(3):1460- 1471.

[13] DOUGLASS D A. Radial and axial temperaure gradients in bare stranded conductor [J]. IEEE Transactons on Power Delivery,1986,1(2):7- 16.

[14] BLACK W Z. Theoretical model for temperature gradients within bare overhead conductors [J].IEEE Transactons on Power Delivery,1988(2):707- 716.

[15] NIGOL O,BARRETT J S. Characteristics of ACSR conductors at high temperature and stresswes [J]. IEEE Transactions on Power Apparatus and Systems,1981,100(2):485- 494.

[16] 王春江．电线电缆手册 [M]．2版.北京：机械工业出版社，2014．

[17] SEPPA T O.Factors influencing the accurate of high temperature sag calculations [J].IEEE Trasactions on Power Delivery,1994,9(2):1079- 1090.

[18] 纽春萍，陈德桂，刘颖异，等．交流接触器温度场仿真及影响因素的分析 [J]．电工技术学报，2007，22(5)：71- 77．

NIU Chun-ping,CHEN Dejia,LIU Ying-yi,et al. Temperature field simulation of AC contactor and analysis of itsi nfluencefactors [J]. Transactions of China Electrotechnical Society,2007,22(5):71- 77

[19] 江淘莎，李剑，陈伟根．油浸式变压器绕组热点温度计算的热路模型 [J]．高电压技术，2009，35(7)：1635- 1640．

JIANG Tao-sha,LI Jian,CHEN Wei-gen. Thermal model for hotspot temperature calculation in oil-immersed transformer [J]. High Voltage Engineering,2009,35(7):1635- 1640.

[20] CHEN Wei-gen,PAN Chong,YUN Yu-xin. Power transformer Top -Oil temperature model based on thermal-elecric analogy heory [J]. European Transaction on Electrical Power,2009,19(3):341- 354.

[21] 刘刚，雷成华，刘毅刚．根据电缆表面温度推算导体温度的热路简化模型暂态误差分析 [J]．电网技术，2011，35(4)：212- 217．

LIU Gang,LEI Cheng-hua,LIU Yi-gang. Analysis on transient error of simplified thermal circuit model for calculating conductor temperature by cable surface temperature [J]. Power System Technology,2011,35(4):212- 217.

[22] 孙国霞，舒乃秋，吴晓文，等．基于多物理场耦合的气体绝缘母线触头接触温升有限元计算 [J]．电工技术学报，2013，28(2)：408- 413．

SUN Guo-xia,SHU Nai-qiu,WU Xiao-wen,et al. Finite element analysis of contact temperature rise in gas insulated busbars based on coupled multi-physics [J]. Transactions of China Electrotechnical Society,2013,28(2):408- 413.

[23] 陶文栓．传热学 [M]．西安：西北工业大学出版社，2006．

[24] 刘刚，阮班义，张鸣．架空导线动态增容的热路法暂态模型 [J].电力系统自动化，2012，36(16)：58- 62．

LIU Gang,RUAN Ban-yi,ZHANG Ming.A transient model for overhead transmission line dynamic rating based on thermal circuit method [J].Automation of Electric Power Systems,2012,36(16):58- 62.

[25] 毛先胤，盛戈皞，刘亚东，等．架空输电线路暂态载流能力的计算和评估 [J]．高压电器，2011，47(1)：70- 74．

MAO Xian-yin,SHENG Ge-hao,LIU Ya-dong,et al. Calculation and evaluation of overhead transmission line transientampacity [J]. High Voltage Apparatus,2011,47(1):70- 74．

[26] 孟遂民，孔伟．架空输电线路设计 [M]．北京：中国电力出版社，2007．

[27] 窦飞，乔黎伟．架空线路输电能力综述 [J].江苏电机工程，2011,30(1)：81- 84．

DOU Fei，QIAO Li-wei.Survey on the transmission capacity of overhead line [J] ．Jiangsu Electrical Engineer,2011,30(1)：81- 84．

EffectofRadialTemperatureDifferenceonSagCalculationforOverheadConductors

LIUGangLIYangCHENYuanYANGYu-hang

(School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China)

In this paper, firstly, a thermal circuit model of ACSR (Aluminium Cable with Steel Reinforcement) was established to analyze the radial temperature field distribution. Secondly, the temperature field of conductor section in different loading conditions was calculated via a finite element analysis. Then, the causes for radial temperature gradient were analyzed through the simulation and were verified by the experiments of temperature distribution on the steel-reinforced layer and the surface. Finally, on the basis of experimental results, the calculation errors of different sags caused respectively by temperature difference and span difference were discussed. It is found that, with the improvement of current carrying capacity, the radial temperature difference increases, leading to the gradual expansion of sag’s calculation error. For example, when the outer temperature achieves 70 ℃, the steel core temperature under natural convection is 73.5 ℃. Moreover, it is found that, at a certain radial temperature difference between the steel-reinforced layer and the surface, greater span may result in larger calculation error and smaller relative error.

overhead conductor; radial temperature difference; finite element analysis; sag

2016- 08- 17

国家高技术研究发展计划(863计划)项目(2015AA050201)

*Foundationitem: Supported by the National High-tech R&D Program of China(863 Program)(2015AA050201)

刘刚(1969-)，男，博士，副教授，主要从事电气设备在线监测与故障诊断、过电压及其防护、电力设备外绝缘技术研究.E-mail:liugang@scut.edu.cn

1000- 565X(2017)07- 0041- 07

TM 715

10.3969/j.issn.1000-565X.2017.07.006