基于GPS双天线的弹体姿态测量方法

丁传炳，卞伟伟，李海滨

(1.中国舰船研究设计中心，上海 201108；2.北京机械设备研究所，北京 100854)

基于GPS双天线的弹体姿态测量方法

丁传炳1，卞伟伟2，李海滨1

(1.中国舰船研究设计中心，上海201108；2.北京机械设备研究所，北京100854)

针对舰载武器弹体飞行姿态信息难以实时准确测定的问题，提出采用GPS双天线配置方案来测量飞行弹体姿态的方法，该方法首先建立用于飞行弹体姿态测定的观测模型，结合对GPS载波相位信息求解基线矢量及整周模糊数解算的分析推导，通过坐标系的变换得到弹体的姿态信息。数值计算表明，弹体的俯仰角误差范围在±0.8°之间；偏航角误差范围在±0.7°之间，计算结果验证了模型和算法的有效性。

舰载炮弹；GPS；差分GPS；姿态测量

0 引言

针对载武器弹体飞行姿态信息测定问题，长期以来一直采用惯性导航系统，且大多是在飞机、导弹等飞行器上的应用[1-2]，对舰载火箭弹或炮弹采用GPS姿态测量系统来获取弹体飞行姿态问题的研究较少，而弹体的姿态信息是导航、制导领域不可缺少的参数信息，传统上，GPS导航系统一般用来测量载体的实时位置和速度信息，且测量设备的组成简单、价格低廉、不受气候影响、误差不随时间积累、实施应用简便等优点。随着GPS导航技术水平的发展，近年来，GPS姿态测量技术逐渐发展和应用起来，它是基于GPS载波相位测量技术发展起来的一种全新的测姿方法。通过在载体上布置多个天线，然后获取各天线的载波相位测量值，再解算天线间各基线矢量，进而得到载体的姿态。但是GPS多天线测姿技术存在着天线安装困难等问题[3]，特别是对于高过载的飞行弹体，采用GPS多天线测姿技术来获取弹体飞行姿态，就更加困难，而安装GPS、双天线则具有较强的可实施性。

本文正是基于GPS双天线姿态测量技术的操作性较强的特点，提出采用GPS双天线确定弹体飞行姿态的方法，对采用双天线测定弹体飞行姿态的原理进行分析研究，并将该测姿算法在测定某舰载武器的飞行姿态进行了仿真计算分析。

1 GPS双天线测姿态原理

GPS测姿技术是通过在飞行载体上设置多天线[3](两个或以上)，通过获取各天线测量GPS载波信号的相位差，实时测定载体坐标系相对于当地地理坐标系的角位置信息，通过数学推导解算出载体的姿态参数。所谓载波信号的相位差就是通过测量基线两端天线GPS的瞬时相位，然后将两载波信号相位作差。通常来说，基线的长度相对于GPS卫星和测量载体之间的距离几乎可以忽略不计，因为可以将GPS载波信号等效看作是平面波，基波的波前平面与卫星视间线相垂直。而基线的长度可以看作是已知量，将基线矢量投影在卫星视间线上，卫星视间线上的载波相位差也就被此投影所决定，它包含整周数和小数相位两部分。如果同时对几个可见卫星观测它们的载波相位差，那么就可以确定基线的空间指向。

2 GPS双天线弹体姿态测量方法

2.1 最小二乘法解算基线向量

为了求解基线向量，首先引入这个概念，所谓的传播延时它是由卫星发送至用户接收机天线的载波信号的传播时间。因此，不难看出传播延时的大小与卫星至天线之间的距离成正比，而距卫星距离相等的两个点上所接收到的卫星载波信号在同一时刻将具有相同的相位，换而言之，若接收卫星信号的两点至可见星的距离不同，那么这两点的相位也不相同，如图1所示。

(1)

当天线1和天线2同时接收GPS卫星j的信号时，就同时得到两个载波相位的观测方程，将两个相位观测方程作差，就可以求取站际单差观测方程，它就是卫星接收天线1和天线2同时观测可见卫星j的载波相位单差，可表示成如下形式：

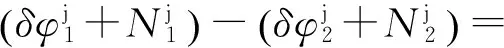
(2)

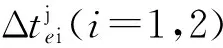
(3)

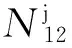
在两接收机天线共视GPS可见星j时，基线向量b12的确定可通过下式：

(4)

式中，Sj为GPS可见星j到接收机天线1和天线2的单位向量(两单位向量可视为相同)；λ为GPS载波信号波长。

根据式(3)和式(4)，当同时有3颗GPS可见星时，基线向量b12就可以求解出来。

2.2 整周模糊数解算

针对整周模糊度的求解方法一般常用的办法有最小二乘搜索算法、模糊函数法等，这些计算方法总体来说都比较复杂，运算量较大，最重要的问题是载体一旦在飞行过程中发生GPS接收机失锁而产生跳周现象，这就势必会出现整周单差无法解算的困难问题[9]。

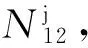
(5)

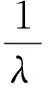
(6)

将式(5)代入式(6)可得：

(7)

将式(12)四舍五入运算：

(8)

因而有：

(9)

2.3 弹体姿态角解算

根据式(3)和式(4)可以将基线向量b12求解出来，用矩阵的形式可以形如下式[4]：

(10)

如果同时对3颗GPS可见星进行观测：j=1，2，3时，可以得到

(11)

当GPS可见星的观测数nj≥4时，可以考虑采用最小二乘法对所以可见星的观测信息进行解算求取基线向量，而且能够得到比选择3颗卫星更高的解算精度。此时式(10)可用误差方程的形式表示，如下式：

(12)

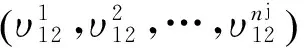
采用最小二乘法平差求解基线向量b12，可得

(13)

前面对于基线向量b12的解算是在协议坐标系(WGS-84)下计算出来的，为了方便对弹体姿态的求解，可以通过相应的坐标变换，将其变换至地理坐标系中进行表示[6]。

根据已经计算得到的基线向量b12，通过图2所示的姿态角变换关系，飞行弹体偏航角ψ、俯仰角θ可以分别表示为[4-5]：

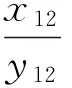
(14)

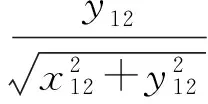
(15)

2.4 系统设计

本文研究的是利用双天线GPS的测量数据，通过数据处理，实时解算出飞行弹体的姿态信息。此测姿系统硬件组成主要由两个GPS天线和一个GPS接收机组成，通过两块OEM板实时读取跟踪到的GPS、卫星载波相位、天线坐标和卫星星历等信息，整个系统的计算流程如图3所示。

3 算例及分析

本文针对双天线GPS对舰载炮弹飞行姿态测量问题进行了计算，为了对GPS可见星进行模拟，首先根据舰载炮弹弹道模型求解出飞行炮弹的三维空间飞行运动轨迹(见图4)，然后模拟每个时间点上GPS可见星的数目和卫星坐标。采用单基线，基线长度为0.36 m，GPS载波相位的量测噪声为5×10-3m，炮弹飞行时间150 s。姿态信息仿真结果见图5-图6。

根据计算结果图5-图6可以看出，采用双天线GPS确定舰载武器的飞行姿态时，其俯仰角误差范围在±0.8°之间；偏航角误差范围在±0.7°之间，误差较小。

为了进一步说明模型和算法的正确性，结合弹载惯性测量装置测得的弹体飞行姿态信息，将仿真计算结果与试验测量结果进行对比(见表1)，由对比表可以看出，采用本文的数学模型和算法计算得到的弹体姿态值与试验采用惯性测量装置测得的值基本吻合，验证了模型和算法的正确性。

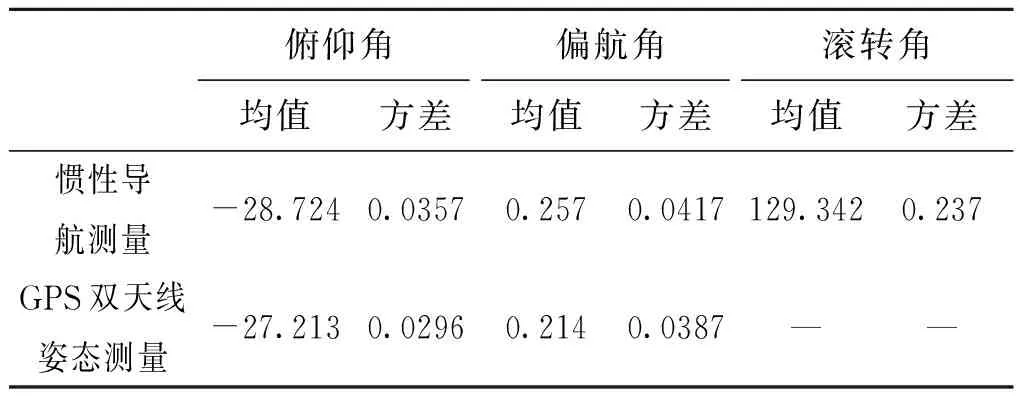
表1 姿态角均值、方差对比

另外，由于本文的GPS双天线是布置在弹体纵轴方向上，可以很好地解决舰载炮弹横向尺寸不足以安装多天线GPS的实际难题，且测量系统具有体积小、成本低、结构简单、重量轻特点，唯一不足的是无法测量飞行弹体的滚转姿态信息。

需要指出的是：受载体自身的特点和GPS接收机性能的影响，双天线GPS姿态测量系统的数据更新率较低(本文的姿态测量数据更新率为0.5 s)，且双天线GPS姿态测量系统无法测定弹体的滚转姿态角。鉴于此，有必要开展对高过载，大频率GPS接收机的研究以及将本文的测姿系统与惯性导航系统进行组合，组成全组合导航系统，从而提高平台失准角和惯性元件误差的估计能力。

4 结论

本文提出采用GPS双天线实时测定舰载制导炮弹飞行弹体姿态信息的方法，该方法通过建立GPS双天线姿态测量的数学模型，结合对GPS载波相位信息求解基线矢量及整周模糊数解算的分析推导，通过坐标系的变换得到弹体的姿态信息。数值计算表明：弹体的俯仰角误差范围在±0.8°之间；偏航角误差范围在±0.7°之间算法的计算精度高、解算速度快，能够很好地满足弹载控制系统对弹体飞行姿态信息量的需求。

[1]曹岩，赵家胜，王伟，等.弹载捷联惯性导航系统算法及仿真[J].西安工业大学学报，2011,31(3):231-235.

[2]彭惠，熊智，刘建业，等.近空间高超声速飞行器惯性导航系统Simulink仿真研究[J].航天控制，2012,30(2):69-74.

[3]纪文章，王宝发.多天线GPS定姿接收机设计与实现近空[J].电子测量技术，2007,10(30)142-145.

[4]吴美平, 胡小平. GPS卫星定向技术[M]. 长沙: 国防科技大学出版社, 2007.

[5]PARK C,TEUNISSEN PETER J G. A baseline constrain-ed LAMBDA method for integer ambigulity resolution of GNSS attilitude determination systems[J]. Journal of Control,Robotics and Systems,2008,14(6):587-594.

[6]Zhen D,STEFAN KNEDLIK,OTMAR LOFFELD. A MATLAB toolbox for attitude determination with GPS multi-antenna systems[J]. GPS Solution,2009,13:241-248.

[7]王惠南. GPS导航原理与应用[M]. 北京: 科学出版社, 2003.

[8]Gang L, Cannon M E, Lachapelle G,et al. Attitude determination in a survey launch using multi-antenna GPS technologies[C]//National Technical Meeting, ION.San Francisco,1993:20-22.

[9]范胜林，秦岭，袁信.GPS姿态系统中周跳的检测及修复方法[J].数据采集与处理，2002,17(1):50-53.

MissileAttitudeMeasurementMethodBasedonGPSDoubleAntenna

DING Chuanbing1，BIAN Weiwei2，LI Haibin1

(1.China Ship Development and Design Center, Shanghai 201108, China; 2.Beijing Machine and equipment Institute,Beijing,100854,China)

Aiming at the problem that it is hard to accurately determine the information of shipborne weapon projectile attitude to real-tim, a method of measuring the attitude of flying projectile using GPS dual antenna configuration scheme was put forward t. The method established the observation model of flying projectile attitude determination, based on GPS carrier phase information solution analysis and baseline vector integer ambiguity solution.the attitude information of the body was obtained by coordinating transformation. The numerical simulation results showed that the pitch angle error of the missile was in the range of the yaw angle error, and the validity of the model and algorithm.

shipboard gun; GPS;differentia GPS; attitude measure

2017-05-10

兵科院重点预研项目资助(20402020101)

丁传炳(1984—)，男，安徽阜南人，博士，工程师，研究方向：水面舰艇作战系统总体技术。E-mail:chuanbingding@yahoo.com.cn。

TJ413.6

A

1008-1194(2017)05-0026-05