不同升温速率对风帽温度分布的影响

谢 磊，席占稳，聂伟荣，黄 刘

(南京理工大学机械工程学院，江苏 南京210094)

不同升温速率对风帽温度分布的影响

谢 磊，席占稳，聂伟荣，黄 刘

(南京理工大学机械工程学院，江苏南京210094)

针对弹药在制造、存贮、运输及实战环境中可能会遭受意外热刺激的问题，对不同升温速率烤燃环境下风帽结构的传热规律进行研究。建立了引信风帽的烤燃模型，根据烤燃试验对不敏感弹药的升温速率要求，选取3.3 K/h，0.02 K/s，0.05 K/s，1 K/s，1.5 K/s等5种不同升温速率，对引信风帽的烤燃过程进行数值分析。利用数值仿真软件Fluent对引信风帽结构的传热过程进行数值模拟,从而获得了引信风帽结构关键部位的温度分布情况。计算结果及分析表明，在烤燃过程中，火焰升温速率对风帽内部温度分布有很大的影响，随着升温速率的增加，风帽内部温度分布的梯度变大，电子元器件发生失效的时间提前。

烤燃；升温速率；风帽；温度分布；数值分析

0 引言

弹药库房、大型舰艇等重要设施，由于意外发生火灾或受到敌方打击酿成的重大灾难，造成己方人员和财产的不必要损失，欧美等发达国家首先注意到了这一现象[1]，开始考虑如何降低弹药对于加热、撞击、弹药攻击等剧烈的外界刺激的敏感性，以提高作战人员、武器装备的生存能力。不敏感弹药[2](IM-Insensitive Munition)就是指具有对加热、冲击、爆轰等外界刺激不敏感或在这种外界刺激下不会引起强烈反应的弹药。

烤燃试验[3]作为不敏感弹药测试评估标准的重要试验，对于弹药与引信设计的安全性评估具有十分重要的意义。随着一些专业数值模拟平台的飞跃发展，数值分析方法成为研究烤燃现象主要的方向之一，国外从20世纪90年代起对含能材料开展大量烤燃数值模拟研究，国内近几年也开展了相应工作。1991年，美国Jones[4]等用FORTRAN语言开发的HEAT软件对小型烤燃弹(SCB)实验进行了一维计算。2004年，国内冯长根[5]等通过软件PHOENICS 3.3对RDX炸药在热烤过程中的热响应情况进行了数值模拟，并利用传热学理论对炸药的热作用过程进行了分析，建立了炸药在烤燃实验中的热作用模型。2009年，王沛等对不同升温速率下火炸药的烤燃过程进行了数值模拟计算[6]，得到烤燃试验样件的温度分布情况，分析出含能材料热安全特性，为烤燃试验结果预测提供了理论依据。2016年，王洪伟[7]等研究了升温速率对限定条件下烤燃弹热起爆临界温度的影响，结果表明，炸药置于恒定高温环境中比慢速加热更加危险，其发生反应的环境温度更低，响应更剧烈，随升温速率的提高，烤燃弹的热起爆临界温度缓慢升高。此外，还有关于约束条件、装药密度、物理界面等因素对含能材料烤燃响应特性影响的报道，然而关于引信方面烤燃试验的研究却鲜有报道。

本文通过借鉴国内外对弹头引信气动热传热过程以及固体火箭发动机烤燃过程的研究情况，建立了引信风帽结构烤燃过程的二维传热数学模型，并通过数值求解的方法分析了升温速率对风帽内部温度场分布规律的影响，为不敏感弹药引信的隔热吸能、泄压结构设计提供理论支持。

1 风帽烤燃传热模型

1.1 物理模型及基本假设

不敏感弹药烤燃试验对引信影响最为明显的两部分是火工品和电子元器件。国内王晓峰[8]等人进行的烤燃试验发现传爆药PBXN-7的反应温度在215 ℃左右，而军品级电子元器件的正常工作温度范围是-55～+125 ℃[9]，因此引信的烤燃试验必须优先考虑在电子元器件发生误触发的情况，虽然引信形状各异，内部各功能模块繁杂，但是引信的电子元器件大多集中在风帽内部。风帽基本形状可以概括为一种带有空腔的锥形旋成体[10]，为了方便研究且不失典型，假设风帽外表面由球面和锥面组成，风帽内部主要由电磁屏蔽罩、灌封体两部分组成。由于风帽及其内部是对称的锥形旋成体，为了减少计算同时也为方便显示其内部温度分布云图，建立1/2风帽二维结构作为计算模型，并对烤燃物理模型采用整体求解计算，烤燃风帽物理模型如图1所示。风帽锥面厚度各处相同均为2 mm，球面半径为10 mm，电磁屏蔽罩的厚度取1 mm，风帽的总长度取90 mm，模拟计算时将风帽外壁设为加热边界与火焰热流进行传热，模拟实验中设置了5个特征点进行观测，记录其温度变化，5个点的位置分布如图1所示，模拟实验将升温速率作为参数变量讨论风帽结构传热特性。根据所建立的计算模型，对风帽烤燃试验作以下简化假设：①灌封体是均质固相，烤燃过程不发生相变；②风帽、电磁屏蔽罩和灌封体各向同性，其物理化学参数均为常数，不随温度变化；③风帽、电磁屏蔽罩和灌封体三者之间紧密接触，无间隙；④模型底面是假想绝热面(观测点1，2，3，4所在面)。

1.2 控制方程及数值计算模型

考虑到风帽是锥形旋成体，温度场具有轴向及角度的对称性，可以采用二维导热方程进行计算，引信风帽在烤燃加热下的传热问题可以简化为如图2所示的外流场—风帽—电磁屏蔽罩—灌封体之间的流固耦合传热问题。

图2中，qw为风帽外表面上受到的烤燃加热热流密度，qr为外表面向环境的辐射热流密度，qe为高温热流向风帽外壁的辐射热流密度，qλ1、qλ2分别为风帽内部不同材料接触面之间的传热热流密度。对于外部高温热流与风帽表面之间的传热，主要体现在两者之间的对流和辐射上，对风帽外表面进行分析，传入风帽外壁的净输入热流密度可表示为：

q=qw-qr+qe

(1)

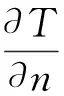
(2)

式(1)、式(2)中，Tw为风帽外壁温度；Tf为火焰温度；h为对流换热系数；σ为黑体辐射常数，其值为5.67×10-8W·m-2·K-1；εw、εf为风帽壁面的辐射率和火焰的辐射率。

根据能量守恒定律和傅里叶导热定律，烤燃环境下风帽二维导热方程在直角坐标系中的基本表达式[11]，如式(3)、式(4)所示。

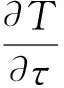
(3)

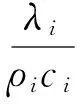
(4)

式中，ai、ρi、λi、ci分别为第i层的扩散系数、密度、导热系数、比热容；T为温度；τ为时间；S为内热源项，烤燃试验中不考虑电子元器件的自发热，内热源项等于0。

风帽内部不同材料之间的导热，由于两种材料接触良好，在两种材料的分界面上的温度相等，可以采用界面连续条件，如式(5)所示。

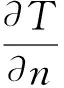
(5)

上述式(1)～(5)构成了风帽及其内部结构的烤燃数学模型。

从式(2)可知影响传入风帽壁面热流密度的主要因素有：火焰温度Tf、风帽壁面辐射率εw、火焰热流的辐射率εf、风帽壁面的对流换热系数h。

火焰温度Tf的确定：根据北约《不敏感弹药评估和研发指南》中对烤燃试验相关要求规定：快速烤燃试验必须以大于1 K/s的升温速度从初始温度快速加热到火焰平均温度1 073 K，并保持20 min，弹药不发生爆轰，慢速烤燃试验则是以小于0.05 K/s的升温速度从初始温度缓慢加热到638 K，弹药不发生爆轰反应，对于引信的烤燃试验而言，完全可以借鉴不敏感弹药的烤燃标准。

对流换热系数h的确定：由于烤燃试验热流场运动的复杂性，目前尚无准确的关联式计算热流与风帽外壁之间的对流换热系数，本论文依据Sandia国家实验室[12]在火烧试验中测得的数值56 W·m-2·K-1作为火焰高温热流与风帽外壁之间的对流换热系数。

考虑到烤燃实验中风帽外壁会被燃料的燃烧熏黑，风帽外壁的辐射率εw和高温热流εf的辐射率取恒定值0.85。

2 计算方法及条件设置

本模拟实验使用Ansys软件中的Fluent进行计算，Fluent是个功能强大、应用广泛的有限体积法数值计算软件，可用于涉及流体、热传递等工程问题的计算分析。本文采用Fluent软件对风帽结构进行二维非稳态热分析，计算内容包括外部高温热载荷与风帽外表面的对流、辐射传热和固体(风帽、电磁屏蔽罩和灌封体)导热，关于对流与导热耦合问题，已有不少文献运用数值方法进行求解并获得较好的计算结果。本次烤燃模拟实验需要通过Fluent提供的用户自定义函数(User-Defined Function，简写为UDF)加载风帽外壁火焰热流的对流和辐射边界条件，风帽、电磁屏蔽罩、灌封体的初始温度为293 K，各结构之间紧密贴合，设定其界面为耦合接触界面。

通常弹头引信的风帽材料多为高分子化合物材料[13]，我国用于弹头引信风帽的高分子材料有聚醚矾、聚矾、聚苯醚、尼龙、聚苯硫醚等工程塑料，而高速飞行弹丸头部引信的风帽材料需要使用铝合金、陶瓷等耐高温材料，对于快速烤燃模拟实验来说，由于火焰温度最高可达到1 073 K，超过了高分子化合物的熔点，显然上述材料已不再适用。本文选择使用能耐受此高温，应用广泛的结构陶瓷材料碳化硅(SiC)作为风帽材料，电磁屏蔽罩选用金属材料铝，灌封体材料选择使用与电子元器件相兼容的环氧树脂，表1是所选材料的热物理性质参数。Fluent在求解压力耦合方程用SIMPLE算法，求解能量方程选择二阶迎风格式，松弛因子选择默认值，在考虑非稳态传热过程计算时间和收敛性的基础上，选择每个时间步长为0.05 s，每个时间步最大伪迭代步数为50步。

表1 风帽材料物性参数

3 计算结果及分析

通过对烤燃过程的模拟实验，数值解算不同升温速率下风帽结构及其内部关键点的温度变化并进行定量分析，将烤燃模拟实验数值解算求得的内部关键点温度与加载温度进行差值分析，不同升温速率下风帽内部观测点温度差值随加载温度的变化曲线如图3所示(温差=加载温度-观测点温度)。其中不管升温速率如何变化，观测点1和观测点2的温差曲线几乎重合在一起，说明风帽与电磁屏蔽罩的传热热阻很小，在烤燃过程中对内部温度分布的影响可以忽略不计。

3.1 升温速率对风帽内部温度梯度的影响

由图3可以看出，当升温速率为3.3 K/h时，整个慢速烤燃过程中，各点的温度与加载温度之间的温差保持不变，几乎为零，因此在3.3 K/h的慢烤试验中可以认为，风帽及其内部的温度趋于一致，整体在同一瞬间均处于同一温度下。当升温速率为0.02 K/s和0.05 K/s时，在初始一段时间内，各点温差值呈明显的上升趋势，随着时间的推移，温差达到相应最大值后，各点温度又以微小的变化趋势向加载温度靠近，温差值与加载温度表现出平缓的线性减小关系。观测点4的温差比其他观测点大，且不同升温速率下，观测点4的最大温差值分别为28 K和62 K。当升温速率为1 K/s和1.5 K/s时，各点与加载温度之间的差值不再有明显的最大值，其差值随温度的增加而不断变大，点3，4，5的温度差值曲线与加载温度基本呈线性关系，点3，5的温差曲线几乎重合在一起。

出现这种现象是因为当升温速率较大时，受到热量扩散速度的限制，内部温度与表面温度温差较大，风帽及其内部结构在不同升温速率下隔热效果有限，同时灌封体在风帽内部具有较好的隔热效果。在升温速率非常小的时，隔热效果几乎可以忽略，此时可以认为风帽整体在同一瞬时与环境温度保持一致，随着升温速率的不断增大，引信风帽表现出较好的隔热效果，风帽内部出现了明显的温度梯度，当升温速率在0.02～0.05 K/s之间时，风帽内部温度梯度有一段时期的平缓区，在平缓期中温度梯度随着时间的增加以较缓的速度减小，随着升温速率的增加，慢速烤燃变为快速烤燃即升温速率达到1 K/s以上时，风帽内部的温度梯度随时间的增加不断增大，此时风帽整体表现出良好的隔热效果，并且温度梯度的平缓期消失了。上述计算结果可以为不同要求的烤燃试验对升温速率的选择提供理论依据。

3.2 升温速率对电子元器件失效的影响

图4(a)给出了加载温度为1 073 K时，风帽表面、灌封体表面、灌封体内部温度的时间变化曲线，图4(b)、(c)给出了不同升温速率下加热到1 073 K不变时，加载温度、风帽外表面温度、灌封体外表面温度、灌封体内部温度的时间变化曲线。电子器件在风帽内部的放置位置各不相同，以风帽内温度最低点4的变化情况为参考，以军用电子元器件极限工作温度125 ℃作为电子元器件的失效温度，从图3可以看出以3.3 K/h，0.02 K/s，0.05 K/s进行慢速烤燃时，电子元器件的失效时的火焰温度(时间)分别为398 K(约1.36×105s)、423 K(7 500 s)、460.5 K(3 750 s)。从图4中可以看出，以1 K/s和1.5 K/s的升温速率加热到1 073 K并保持不变时，电子元器件失效时间变为830 s和710 s，加载温度恒定保持为1 073 K时，超过电子元器件工作温度的响应时间大约为420 s。由此可知，随着升温速率的增大，灌封体对加载温度的响应越快，电子元器件发生失效的时刻提前。

4 结论

本文对不同升温速率烤燃环境下风帽结构的传热规律进行研究。建立了引信风帽的烤燃模型，根据烤燃试验对不敏感弹药的升温速率要求，选取3.3 K/h，0.02 K/s，0.05 K/s，1 K/s，1.5 K/s等5种不同升温速率，对引信风帽的烤燃过程进行数值分析。利用数值仿真软件Fluent对引信风帽结构的传热过程进行数值模拟,从而获得了引信风帽结构关键部位的温度分布情况。计算结果及分析表明：

1)在引信烤燃过程中，火焰的升温速率对风帽结构内部温度分布有很大影响，随着升温速率的增加，风帽内部的温度梯度不断增大。

2)火焰的升温速率对风帽内部电子元器件发生失效的时间有显著的影响，火焰升温速率越大，电子元器件的失效时间越早。

3)烤燃环境下，灌封体的隔热效果较好，风帽与电磁屏蔽罩对温度传递的影响极小，可以忽略。

[1]邹金龙, 雷雅茹. 不敏感弹药对引信技术的要求内涵[J]. 探测与控制学报, 2016, 38(1):1-6.

[2]张春海. 不敏感弹药,让士兵和武器更安全[J]. 现代军事, 2006(2):54-59.

[3]梁晓璐, 梁争峰, 程淑杰,等. 不敏感弹药试验方法及评估标准研究进展[J]. 飞航导弹, 2016(6):84-87.

[4]Jones D A, Parker R P. Heat flow calculations for the small-scale cook-off bomb test, DA236829[R]. US: DTIC,1991.

[5]冯长根, 张蕊, 陈朗. RDX炸药热烤(Cook-off)实验及数值模拟[J]. 含能材料, 2004, 12(4):193-198.

[6]王沛, 陈朗, 冯长根. 不同升温速率下炸药烤燃模拟计算分析[J]. 含能材料, 2009, 17(1):46-49.

[7]王洪伟, 智小琦, 郝春杰,等. 升温速率对限定条件下烤燃弹热起爆临界温度的影响[J]. 含能材料, 2016, 24(4):380-385.

[8]王晓峰, 戴蓉兰, 涂健. 传爆药的烤燃试验[J]. 火工品, 2001(2):5-7.

[9]周婕, 刘鉴莹, 何冰.军品型号用塑封工业级元器件的可靠性控制研究[J].电子质量, 2014(5):16-19.

[10]齐杏林, 余春华, 高敏,等. 弹头引信风帽内表面温度影响因素[J]. 探测与控制学报, 2015(2):15-18.

[11]杨世铭，陶文铨.传热学第四版[M].北京：高等教育出版社,2006:4-15.

[12]Planas-Cuchi E, Casal J. Modelling temperature evolution in equipment engulfed in a pool-fire[J]. Fire Safety Journal, 1998, 30(3):251-268.

[13]张维莹. 某小口径弹头引信风帽失效问题的内应力研究[D]. 南京：南京理工大学, 2008.

DifferentHeatingRatesEffectingFalseCapTemperatureDistribution

XIE Lei, XI Zhanwen, NIE Weirong, HUANG Liu

(School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing, 210094,China)

In ammunition manufacture, storage, transportation and combat environment, thermal stimulation may occur accidentally. With different heating rates of cook-off, heat transfer rule of the fuze’s false cap structure should be studied. According to requirement of cook-off test, the physical cook-off model of fuze’s false cap is built and the heat transfer process of fuze’s false cap at different heating rates such as 3.3 K/h, 0.02 K/s, 0.05 K/s, 1 K/s, 1.5 k/s were simulated. Based on the established model, heat transfer process was calculated by numerical simulation software FLUENT to obtain the temperature distribution in the key parts of the fuze’s false cap structure. Numerical simulation and the results showed that the flame heating rate had great effects on the temperature distribution inside the fuze’s false cap. With the heating rate increasing, the gradient of temperature distribution inside the fuze’s false cap was increased and the failure of electronic components was ahead of time.

cook-off; heating rates; false cap; temperature distribution; numerical analysis

2017-04-15

国家自然科学基金项目资助(51475245)

谢磊(1993—)，男，江苏泰州人，硕士研究生，研究方向：探测制导与控制。E-mail:2431824162@qq.com。

TJ430

A

1008-1194(2017)05-0031-05