基于处理增益的连续波多普勒引信干扰效能分析方法

郭云鹏，闫晓鹏，李 泽，李 冉

(1.陆军装备部科研订购局，北京 100072；2.北京理工大学机电学院，北京 100081)

基于处理增益的连续波多普勒引信干扰效能分析方法

郭云鹏1，闫晓鹏2，李 泽2，李 冉2

(1.陆军装备部科研订购局，北京100072；2.北京理工大学机电学院，北京100081)

针对国内外研究关于连续波多普勒引信的干扰有效性只作了大量的定性描述，几乎没有合适的量化表征参量的问题，提出了以处理增益为表征参量的分析方法，得到了连续波多普勒引信干扰波形的参数选择依据。该方法理论推导了射频噪声干扰、噪声调幅干扰、噪声调频干扰、正弦波调幅干扰、正弦波调频干扰、三角波调幅干扰和三角波调频干扰作用下连续波多普勒引信的处理增益，并进行了仿真验证。定量分析和仿真结果表明：针对连续波多普勒引信来说，调幅类干扰信号干扰效能明显优于调频类干扰信号，干扰信号的调制频率要尽量与引信多普勒频率一致。

连续波多普勒引信；处理增益；干扰效能；调幅干扰；调频干扰

0 引言

连续波多普勒引信由于结构简单、体积小、成本低的特点，至今仍被广泛应用于常规弹药武器中[1-2]。早在上世纪四十年代，无线电引信诞生之初就有了针对无线电引信干扰的技术研究[3]。连续波多普勒引信作为目前主流装备的引信体制之一，针对其干扰技术的研究一直没停止过[4-6]。文献[4]从自差机理论出发，研究了模拟回波对连续波多普勒引信的干扰有效性；文献[5]仿真研究了高斯白噪声干扰对连续波多普勒引信的干扰效果；文献[6]从干扰信号频谱的角度，分析了扫频式干扰对连续波多普勒引信的干扰机理。

无线电引信具有瞬时工作、一次作用的特点，这就对干扰波形的有效性提出了很高的要求。国内外文献对干扰波形的有效性只作了大量的定性描述，但几乎没有量化的对比，这是因为缺乏合适的量化表征参量。处理增益体现了引信系统对干扰信号的抑制能力[7-12]，同时由于处理增益是基于干扰波形获得的，因而也可用来量化对比不同干扰波形的干扰效果。

为此，本文以处理增益为表征参量，对典型干扰波形作用于连续波多普勒引信的干扰效果进行量化分析。

1 连续波多普勒引信工作原理

连续波多普勒引信是一种非调制连续波体制的无线电引信，其基本工作原理框图如图1所示。它首先向目标发射一定能量的电磁波，当电磁波遇到目标后部分能量被反射回引信的接收端，目标回波信号同本振信号进行混频检波得到含有目标信息的多普勒信号，引信对多普勒信号进行信号处理进而感知识别目标并适时引爆战斗部。

连续波多普勒引信发射信号为：

St(t)=Atcos(2πf0t+φ0)

(1)

式中，At为发射信号幅值，f0为载频频率。

引信接收到的回波信号为：

Sr(t)=λAtcos[2πf0(t-τ)+φ0]

(2)

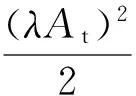
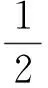
(3)

式中，λ为空间传播损耗因子，τ为回波信号相对发射信号的延迟时间；k为混频系数。

混频信号经由多普勒带通滤波器，高频分量被滤除，得到目标的多普勒信号的功率表达式：

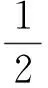
(4)

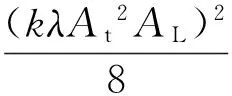
对地无线电引信获的多普勒信号幅值会随着弹目距离的减少而增大，当达到预定幅值且多普勒频率落入多普勒通频带内时，引信会给出起爆信号，从而触发执行机构。

根据连续波多普勒引信工作原理，本文考虑射频噪声干扰、噪声调幅干扰、噪声调频干扰、正弦波调幅干扰、正弦波调频干扰、三角波调幅干扰和三角波调频干扰这七种典型干扰作用下连续波多普勒引信的处理增益。

2 典型干扰波形对连续波多普勒引信的干扰效果

处理增益G定义为系统的输出信干比SJRO与输入信干比SJRi的比值，即G=SJRO/SJRi，体现了引信对干扰信号的抑制能力。同时由于处理增益是基于干扰波形的，因而也可用来表征不同干扰波形对引信的干扰效果。本文理论推导了几种典型干扰波形作用于连续波多普勒引信的处理增益，并通过仿真对其干扰效果进行了量化研究。

2.1 射频噪声的干扰效果

设引信高频振荡电路通带宽带为BH，则引信实际接收到的噪声可视为高斯窄带噪声，时域表示为[10]：

J(t)=Un(t)cos[2πfjt+φ(t)]

(5)

若引信接收端高斯白噪声功率密度为N0，则其接收到的噪声功率为PJi=2BHN0，引信输入信干比：

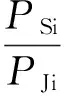
(6)

(7)

于是引信的输出信干比：

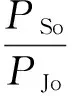
(8)

射频噪声干扰作用下引信的处理增益：

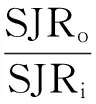
(9)

2.2 噪声调幅信号的干扰效果

噪声调幅信号可以表示为[9]：

J(t)=[Uj+Un(t)]cos(2πfjt+φn)

(10)

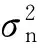
Pn=2FnN0

(11)

由噪声调幅干扰信号J(t)表达式，可得其平均功率为：

(12)

若引信高频振荡电路带宽为BH，则引信实际接收到的干扰信号的功率为：

(13)

引信输入信干比为：

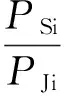
(14)

噪声调幅干扰信号同引信本振信号混频后经过带宽为BS低通滤波器后，输出信号功率为：

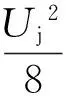
(15)

引信输出信干比为：

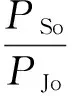
(16)

噪声调幅干扰作用下引信处理增益为：

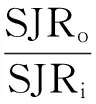
(17)

2.3 噪声调频信号的干扰效果

噪声调频干扰信号可表示为[10]：

(18)

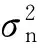
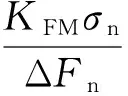
(19)

设引信振荡器通带宽度为BH，通带范围为[fL,fH]，则引信接收到的干扰功率为：

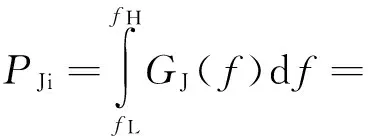
(20)

式中，Φ(x)表示标准正态分布随机变量的分布函数。引信的输入信干比：

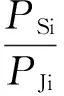
(21)

噪声调频信号同引信本振信号混频，并经滤波器后得到：

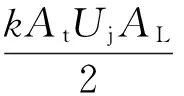
(22)

设引信多普勒低通滤波器的通带截止频率为flp，则引信实际输出的干扰信号的总平均功率为：

(23)

于是引信输出信干比：

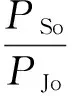
(24)

则噪声调频干扰作用下引信的处理增益为：

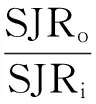
(25)

2.4 正弦波调幅信号的干扰效果

正弦波调幅干扰信号可表示为：

J(t)=Aj[1+macos(2πfdjt)]×cos(2πfjt+φj)

(26)

其中，Aj为干扰信号幅值，ma为调制深度(0≤ma≤1)，fdj为调制信号频率，fj为干扰信号载波的频率，φj为干扰信号相位。所以，干扰信号的输入功率为：

(27)

则输入信干比为：

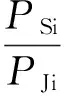
(28)

正弦波调幅信号与引信本振信号混频，并经过多普勒低通滤波，可得输出信号为：

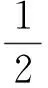
(29)

所以，干扰信号输出功率为：

(30)

输出信干比为：

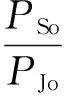
(31)

则正弦波调幅干扰作用下引信的处理增益为：

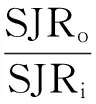
(32)

2.5 正弦波调频信号的干扰效果

正弦波调频干扰可以表示为：

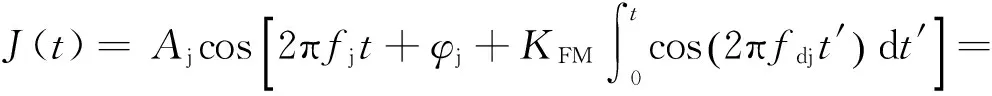
(33)

其中，Aj为干扰信号幅值，KFM为最大频偏，mF为调频指数，fj为干扰信号载波的频率，fdj为调制信号频率，φj为干扰信号相位，Jn(mF)为n阶贝塞尔函数。由贝塞尔函数的性质可知，干扰信号的输入功率为：

(34)

所以输入信干比为：

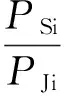
(35)

正弦波调频信号与引信本振信号混频，并经过多普勒低通滤波，可得输出信号为：

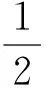
(36)

由上式，干扰信号输出功率

(37)

所以输出信干比为：

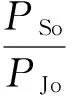
(38)

则正弦波调频干扰作用下引信的处理增益为：

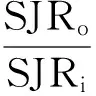
(39)

2.6 三角波调幅信号的干扰效果

三角波信号可以表示为如下傅里叶级数的形式：

(40)

那么，三角波调幅干扰信号可表示为：

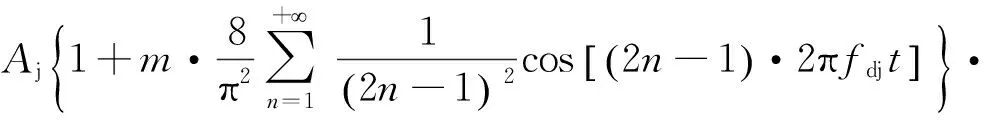
(41)

其中，Aj为干扰信号幅值，m为调制深度(0≤m≤1)，fdj为调制信号频率，fj为干扰信号载波的频率，φj为干扰信号相位。

则输入端干扰信号的功率为：

(42)

那么，输入信干比为：

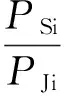
(43)

三角波调幅信号与引信本振信号混频，并经过低通滤波器，可得输出信号为 ：

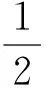
(44)

其中，AL是低通滤波器的增益。则输出干扰信号的功率为：

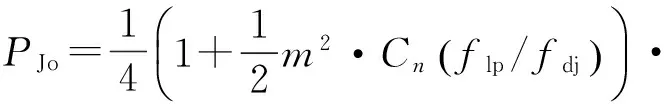
(45)

那么，输出信干比为：

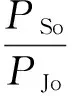
(46)

则三角波调幅干扰下引信的处理增益为：

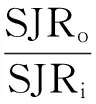
(47)

2.7 三角波调频信号的干扰效果

三角波信号可表示为：

(48)

其中，Tj=1/fdj，fdj为调制信号频率。那么三角波调频干扰信号可表示为：

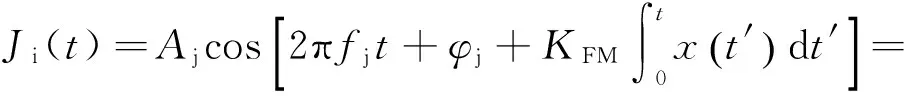
(49)

那么，输入信干比为：

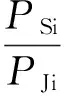
(50)

三角波调频信号与引信本振信号混频，并经过低通滤波器，可得输出信号为：

(51)

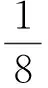
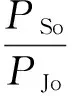
(52)

则三角波调频干扰作用下引信的处理增益为：

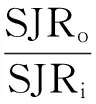
(53)

上述理论推导获取的不同干扰信号作用下连续波多普勒引信处理增益，汇总如表1所示。

表1 不同干扰信号作用下连续波多普勒引信处理增益

3 仿真与试验

3.1 仿真验证

根据连续波多普勒引信的工作原理，构建了基于MATLAB的引信仿真模型，并对7种干扰波形作用效果进行了仿真验证，计算其处理增益。仿真验证具体步骤如下：

1)根据多普勒引信的工作原理构建Simulink仿真模型，如图2所示。仿真工作参数设置如下：引信载波频率f0=500 MHz，高频振荡电路通带宽带BH=5 MHz，对应接收频带范围197.5～502.5 MHz，多普勒低通滤波器截止频率为flp=1 MHz，即BS=1 MHz，信号幅值为1 V，信号处理各级系数为1；

2)选择干扰信号的形式(见表2)，仿真参数如表3备注所示；

3)每次仿真时间为50 ms；

4)记录仿真数据并计算处理增益。

表3给出了不同干扰波形作用下连续波多普勒引信处理增益的仿真结果。可见，针对连续波多普勒引信开展的不同干扰波形作用下引信处理增益计算和仿真值一致，证明了解析表达式的正确性。理论计算和虚拟仿真得到的各干扰波形的干扰效果由好到坏依次为：正弦波调幅干扰、三角波调幅干扰、

噪声调幅干扰、三角波调频干扰、正弦波调频干扰、噪声调频干扰、射频噪声干扰。

3.1 干扰效果试验测试

为进一步验证理论推导和仿真分析所得结论，本文在微波暗室内测试了各种干扰波形对某连续波多普勒引信的干扰效果，试验中干扰系统与引信的空间位置不变。试验测试结果如表2所示，试验参数设置同表3备注。

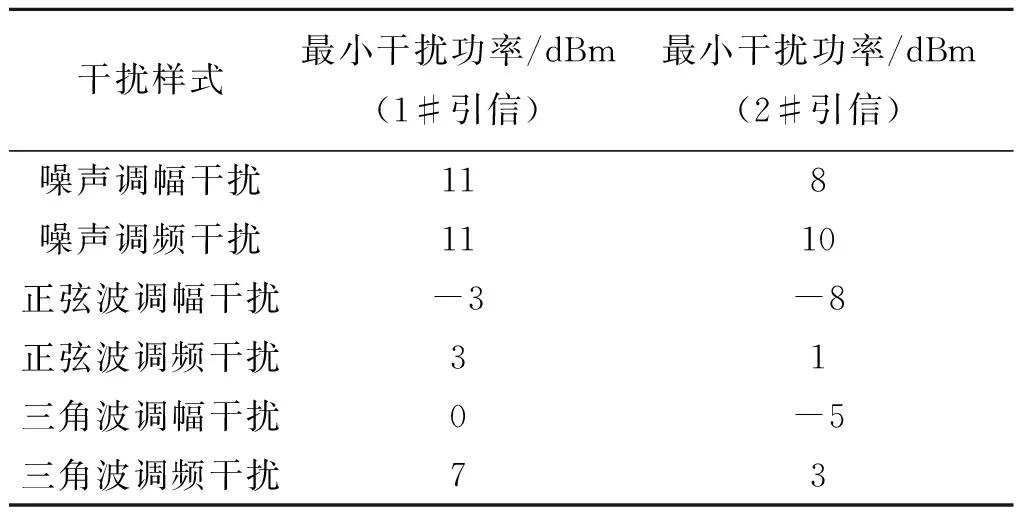
表2 干扰波形下引信启动的最小干扰功率测试结果

表3 不同干扰波形作用下连续波多普勒引信处理增益计算和仿真值对比

由表2可见，能使引信启动的干扰功率越小的干扰波形干扰效果越好，因此，调幅类干扰样式干扰效果明显优于调频类干扰信号。

4 结论

本文以处理增益为表征参量，对典型干扰波形作用于连续波多普勒引信的干扰效果进行了定量分析，为连续波多普勒引信干扰波形设计提供了理论依据。理论推导、仿真和试验测试表明多种干扰波形对连续波多普勒引信都有一定的干扰效果。同等干扰功率下，各干扰波形的干扰效果由好到坏依次为：正弦波调幅干扰、三角波调幅干扰、噪声调幅干扰、三角波调频干扰、正弦波调频干扰、噪声调频干扰、射频噪声干扰。因此，在进行连续波多普勒引信干扰波形设计时，应优先选择调幅类干扰信号，调制频率要根据对抗目标的多普勒频率范围来确定。

[1]崔占忠, 宋世和, 徐立新. 近炸引信原理[M]. 第 3 版 . 北京: 北京理工大学出版社, 2009.

[2]赵惠昌. 无线电引信设计原理与方法 [M]. 北京 : 国防工业出版社, 2012.

[3]韩传钊, 施聚生, 杨平. 模拟回波对自差式多普勒引信的干扰有效性研究 [J]. 北京理工大学学报, 1998,18(5):600-604.

[4]艾娜, 马伯渊. 外差式连续波多普勒引信干扰波形设计 [J]. 航天制造技术, 2004, 12(6):41-45.

[5]罗德宏, 孙永泽,郭东敏,等.模块化的连续波多普勒引信信号处理仿真平台[J].探测与控制学报, 2014(3):60-63.

[6]张彪, 闫晓鹏, 栗苹, 等 . 基于支持向量机的无线电引信抗扫频式干扰研究 [J]. 兵工学报, 2016, 37(4):635-640.

[7]周新刚, 赵惠昌,邓建平,等.连续波线性调频引信中多普勒频率抑制研究[J].探测与控制学报, 2007,29 (5):44-47.

[8]闫岩, 崔占忠. 超宽带无线电引信抗干扰性能研究 [J]. 兵工学报, 2010, 31(1):13-17.

[9]周新刚, 赵惠昌, 邓建平,等 连续波线性调频引信中多普勒频率抑制研究 [J].探测与控制学报, 2007,29(5):44-47.

[10]周新刚, 赵惠昌, 涂友超, 等 . 基于多普勒效应的伪码调相及其与PAM复合引信的抗噪声性能分析[J]. 电子与信息学报, 2008, 30(8):1874-1877.

[11]李泽, 栗苹, 郝新红, 等. 脉冲多普勒引信抗有源噪声干扰性能研究[J]. 兵工学报, 2015, 36(6):1001-1008.

[12]赵国庆. 雷达对抗原理[M]. 第二版. 西安:西安电子科技大学出版社, 2012.

AnalysisofCWDopplerFuzeJammingPerformanceBasedonProcessingGain

GUO Yunpeng1，YAN Xiaopeng2，LI Ze2，LI Ran2

(1.Scientific Research and Procurement Bureau of Army Equipment, Beijing 100072, China； 2.School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)

The research on interference effectiveness of CW Doppler fuze is lack of suitable quantitative characterization parameter. To solve the problem, the jamming effect of typical jamming waveform on continuous wave Doppler fuze were quantitatively analyzed based on the characterization parameters of processing gain. The CW Doppler processing gains under the radio frequency noise jamming, noise AM(amplitude modulation) jamming, noise FM(frequency modulation) jamming, sine-wave AM jamming, sine-wave FM jamming, sine-wave jamming, triangle-wave AM jamming, triangle-wave FM jamming were theoretically deduced, and the simulation verifications were carried out. The quantitative analysis and simulation results indicated that, for the CW Doppler fuze, jamming effects of AM signals were obviously better than those of FM signals, and it's necessary to adjust the modulation frequency to match the Doppler frequency.

CW Doppler fuze; processing gain; jamming performance; AM jamming; FM jamming

2017-03-10

郭云鹏(1978—)，男，山西曲沃人，硕士，工程师，研究方向：信息系统顶层设计和规划。E-mail：htcmisslv@163.com。

TJ434

A

1008-1194(2017)05-0020-06