活学活用 克服思维定势*
——兼谈2017年浙江省数学高考解答题
●
(台州市第一中学,浙江 台州 318000)
活学活用克服思维定势*
——兼谈2017年浙江省数学高考解答题
●洪昌强
(台州市第一中学,浙江 台州 318000)
2017 年浙江省数学高考解答题的题型似乎都比较熟悉,但解题方法灵活多样,尤其注重批判性思维的考查,要求考生活学活用,克服思维定势.
高考; 解答题; 思维定势
2017年是浙江省数学高考文理合卷首年,试卷设计在注重数学综合素养考查的同时,关注思维能力的层次性考查,试题比较性测试功能明显.试卷总体难度较近几年有所降低,但与全国或各省(市)卷相比较还具有一定的难度,尤其是解答题的第19,21,22题这3道题,多数考生反映失分较多(据评卷抽样统计:这3道题难度系数分别为0.6,0.37,0.2).为什么学生在这3道题上失分较多呢?导致失分的原因何在呢?笔者就此谈谈个人的一些见解.
1 向量法被先入为主

图1
例1如图1,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
1)证明:CE∥平面PAB;
2)求直线CE与平面PBC所成角的正弦值.
(2017年浙江省数学高考试题第19题)
空间向量为解决立体几何问题提供了一种工具,当下的立体几何教学中,对空间的角和距离计算偏重于向量法.受思维的惯性作用,大多数学生选用了向量坐标法.如图1,“如何建立空间直角坐标系?怎样求点P,E的坐标?”这是解决问题的关键.根据条件,多数学生把原点选在AD的中点N,此时,空间几何能力较弱的学生错误地把点P当作z轴上的点进行处理.也有部分学生知道点P不在z轴上,但如何求出点P,E的坐标并不轻松.题目条件提供了“PC=AD=2DC=2CB”,“怎样将这个条件用好”,即“如何将已知条件PC的长度关系转化到求点P,E的坐标”,部分学生感到有一定难度.一些考生就因为这道题出乱,不仅在时间上耗损了不少,而且在心理上造成过度紧张,影响了全局得分.
在教学中由于过度强化了向量法的作用,几何法的应用被削弱,学生的解题思维易被坐标法“套”住.若对一种方法过于强化,个性思维遭到压抑,造成解题思路单一,尤其面临新情境下的问题,受原有条条框框影响,按老套路行事,无法实现对原有认识和方法的超越,从而感到束手无策,难以改变现状.在立体几何教学中,教师在内容的选择、题目的难度要求以及解题方法的指导等方面,如何把握几何综合法和向量坐标法的“度”,及怎样培养学生灵活运用这两种方法,这都是高中数学教师所面临的十分具有挑战性的课题.
2 二面角被隐退到幕后
四棱锥P-ABCD可以看成是由△PAD和直角梯形ABCD沿AD翻折而成的.翻折到什么位置,条件中没有直接告知二面角P-AD-C的大小,而是通过由PC=AD来求出.这样问题就缺少了二面角的背景,削弱了条件“PC=AD”在求直线CE与平面PBC所成角的作用,增大了解题难度.此题若把条件“PC=AD”换成“二面角P-AD-C为120°”,学生自然会想到先作出二面角的平面角.有了这个背景,不仅PC易求,而且更易想到把求点E到平面PBC的距离,转化为在△PNB中求点Q(或点N)到PB的距离.同样地,在使用向量法进行处理问题时,若有了二面角P-AD-C的平面角∠PNB的背景,则给求点P的坐标带来了很大方便.虽然新高考降低了求二面角的要求,但二面角是空间几何中面与面之间的一种重要的位置关系,空间几何的研究与二面角息息相关.本题由于条件没有直接提到二面角,而是让二面角隐退到幕后,部分学生对问题情境发生改变或表面上稍作变动感到陌生,知识联系发生断链,信息之间无法进行交互转换,最后导致解题思路出现受阻.
3 弦长公式被“弦”蒙住

图2
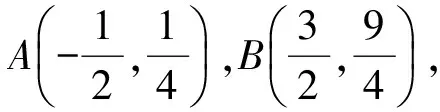
1)求直线AP斜率的取值范围;
2)求|AP|·|PQ|的最大值.
(2017年浙江省数学高考试题第21题)

4 向量数量积几何意义逆用被忽视

5 数与形被分离

解析几何是用代数方法研究几何,只不过研究工具是代数方法,问题的根源还是几何.若能充分利用几何的特性,数与形巧妙结合,解题往往会产生出奇制胜的功效.本题在垂直的环境下,研究两条线段长度之积.“垂直”是几何中最重要的数学核心概念之一,其内涵十分丰富,随知识的增长对其理解也应不断深入.根据答题情况来看,学生对垂直的理解还是比较浅薄.如何更有效地落实数学核心概念教学,是每位数学教师值得探究的课题.
6 逆向思维被削弱
例3已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(其中n∈N*),证明:当n∈N*时,
1) 0 (2017年浙江省数学高考试题第22题) 导致本题失分的原因是多方面的,其主要原因是:新的问题情境带来的紧张心理.解答题的压轴题难度虽然较大,但第1)小题对中等以上水平的学生来说还是可以拿分的.本题所给出的递推关系xn=xn+1+ln(1+xn+1),与平时所做过的数列递推题目的类型xn+1=f(xn),存在一定差距,增加了陌生感,再加上要把xn=xn+1+ln(1+xn+1)转化为xn+1=f(xn)又有一定的困难,难免会产生解题畏惧心理.另外,学生缺乏逆向思维训练.要从xn>0推出xn+1>0,即由xn+1+ln(1+xn+1)>0得到xn+1>0.若从正向去想,不易直接推出所要的结论.此时需要变换角度,换个方法思考,用反证法可使问题变简单,从而轻松得到结果. 即证f(x)=x2-2x+(x+2)ln(1+x)在[0,1)上单调递增,且f(0)=0. 由于此式结构比较复杂,xn与xn+1“纠缠”在一起,较难得出xn与xn+1有“好”的关系.采用以退求进,先对式子变形,得 即 这3道试题表面上看题型似乎都比较熟悉,但解题思维方法灵活多样,需要学生对题目条件和结论有较深刻理性的认识,才能准确理解题意、正确判断解题方向.数学高考关注了发散性、批判性思维的检测,体现了试题对高层次理性思维和创新思维的考查,让凭借题海战术或重复操练学数学的考生在高考中占不了便宜,走老套路会吃亏.这就是2017年浙江试卷的亮点之一.同时,教师要转变教学观念,学生的成长需要经历过程,而不是依靠教师就能把知识送给他们.教学中应注重引导学生自主学习,活学活用,鼓励学生敢于质疑,大胆探索问题,标新立异,培养学生创造性思考和独立解决问题的能力,切忌让学生盲目跟着老师,避免学生的思维被教师控制. 2017-09-01 洪昌强(1963-),男,浙江台州人,中学高级教师.研究方向:数学教育. O123. 2 A 1003 - 6407(2017)11-43-03
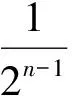
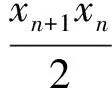
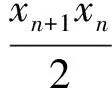


7 结束语

