寻图形之关联 搭模型之框架*
——“一线三等角”模型中考试题归类赏析及启示
●
(曙光中学,浙江 宁波 315040)
寻图形之关联搭模型之框架*
——“一线三等角”模型中考试题归类赏析及启示
●胡伟斌
(曙光中学,浙江 宁波 315040)
在2017 年的各地数学中考试卷中,涌现出不少可用同一类基本模型求解的试题. 这些试题虽呈现的背景、条件和问题互不相同,但解法类似,这就要求教师通过研究试题来挖掘并提炼其中蕴藏的基本模型,从而实现“掌握模型,举一反三,通一类题”.
一线三等角; 中考试题; 归类赏析
1 缘从何起
在近些年的数学中考复习中,模型教学与渗透越来越受到广大数学教师的关注,而在众多的基本模型中,相似模型因其种类多、图形美、内涵丰富,常常成为各类公开课和展示课上的“嘉宾”.而“一线三等角”模型作为其中的“翘楚”,更是受到了许多中考命题者的青睐,以其为基本框架而精心设计的试题,在近些年各省市的中考中,屡见不鲜,精彩纷呈.其中有些试题,“一线三等角”直接跃然于纸上,让人一目了然,茅塞顿开;另有部分试题,“一线三等角”并非直观呈现,而是隐藏在所给的图形中,这就需要我们通过观察辨别和分析探究,合理地予以构造,挖掘出图中隐藏的“一线三等角”.但无论模型是“显”亦或“隐”,试题之精彩让笔者留下了深刻的印象.基于此,笔者收集并整理了2017年可用“一线三等角”模型求解的部分中考试题,并对其进行分类赏析,与同仁们分享.
2 模型呈现
如图1和图2,在△ABC和△CDE中,点C是直线BD上的点.若∠ACE=∠ABD=∠EDF,则△ABC∽△CDE.特别地,当AC=CE时,△ABC≌△CDE.
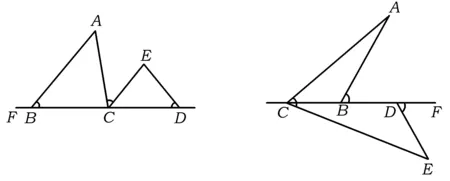
图1 图2
上述两个图呈现的是两种最典型的“一线三等角”模型,即同侧型和异侧型,两者所求证的结论均可通过导角证明.该模型最本质的特点为:有3个等角的顶点在同一条直线上,且这个角可以是锐角、直角或钝角.而随着角顶点位置的适当改变或角绕顶点旋转一定角度,常会产生许多和谐美观的图形,且结论仍然成立.正因如此,近年来各地命题专家们命制了许多可用“一线三等角”模型求解的中考试题,这些试题大都突出对学生能力与思维的考查,重视数学经验与思想方法的获得,常常具有较高的区分度.
3 试题赏析
类型1三角齐见,模型自现
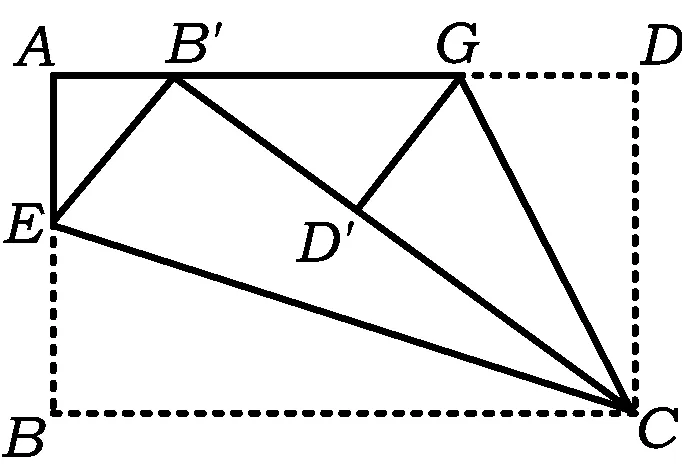
图3
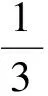
(2017年山东省潍坊市数学中考试题第18题)
分析因为∠A=∠EB′C=∠D=90°,且点A,B′,D在同一直线上,由“一线三等角”模型,得△AEB′∽△DB′C,则
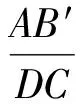
若设AB′=x,则
CD=CD′=3x,
由此可得CB′=CB=AD=3x+2,
从而
B′D=2x+2.
易得
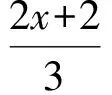
于是
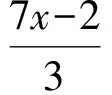
进而
CB′=3B′E=7x-2=3x+2,
解得x=1,故矩形纸片ABCD的面积为15.
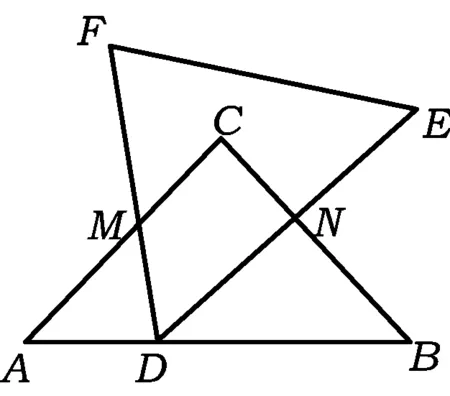
图4
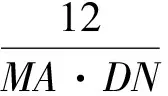
(2017年四川省绵阳市数学中考试题第17题)
分析由于∠A=∠MDN=∠B,且点A,D,B在同一直线上,因此根据“一线三等角”模型可得△MAD∽△DBN,则
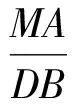
即
MA·DN=DB·MD=4MD,
故
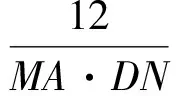

评注以上两例都是典型的“一线三等角”试题,由于模型的框架已搭建,因此降低了试题的起点.两道题虽涉及不同的图形变换,但解法本质一致,均为利用模型构建比例式解决问题.两道题都着重考查学生在图形变换过程中的观察理解、直观感知、推理转化等数学能力和思想.
类型2隐藏局部,小修小补
例3如图5,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为
( )
(2017年山东省泰安市数学中考试题第14题)
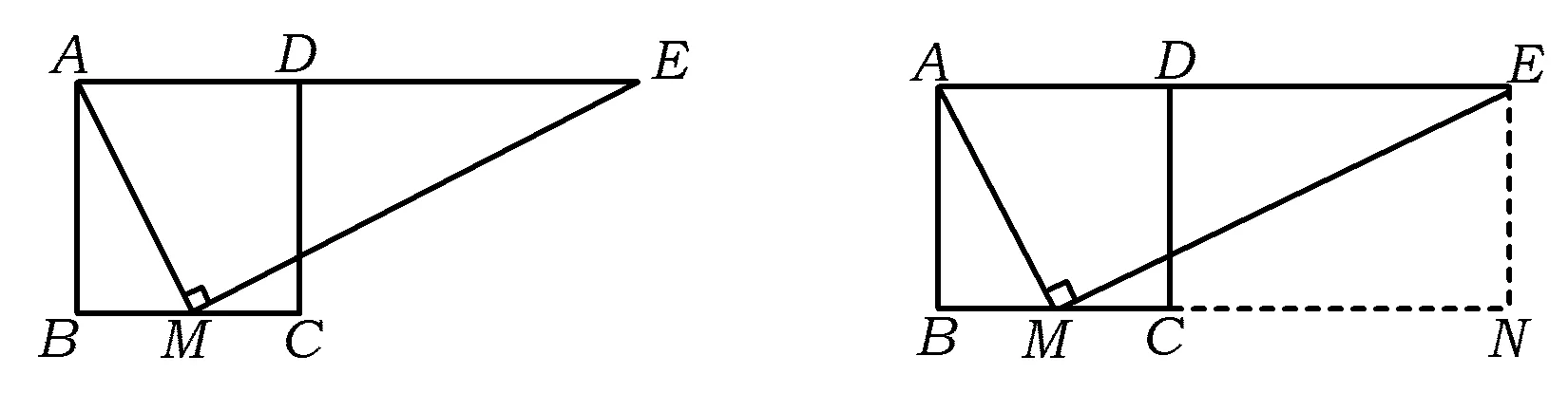
图5 图6
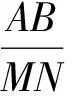

例4如图7,在平面直角坐标系xOy中,直线y=-x+m分别交x轴、y轴于点A,B,已知点C(2,0).
1)当直线AB经过点C时,点O到直线AB的距离是______;
2)设点P为线段OB的中点,联结PA,PC,若∠CPA=∠ABO,则m的值是______.
(2017年浙江省丽水市数学中考试题第16题)
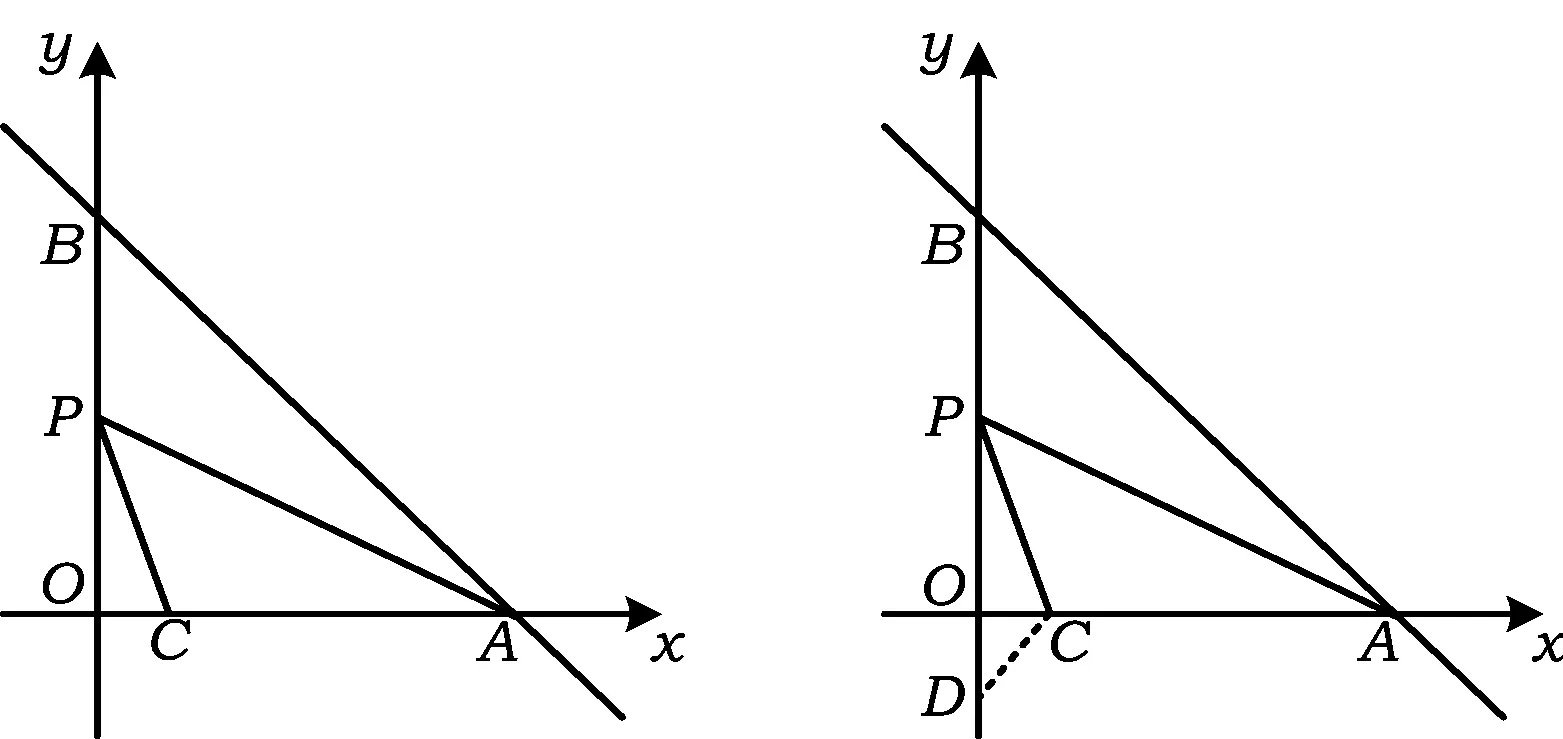
图7 图8

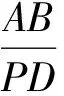
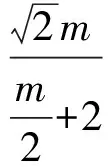
解得m=12.
评注上述两道题虽分别以四边形和一次函数为命题背景,但图形的共性较明显:均将原有“一线三等角”模型中的一角进行了隐藏,而这就要求学生理性地从图形的角度进行思考与联想,发现其中最本质的特征,挖掘蕴含在图中的几何模型.两道题均较好地体现了对“四基”的综合考查,提升了学生思维的层次性和灵活性.
类型3一角独处,两侧添补
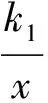
(2017年湖南省株洲市数学中考试题第17题)
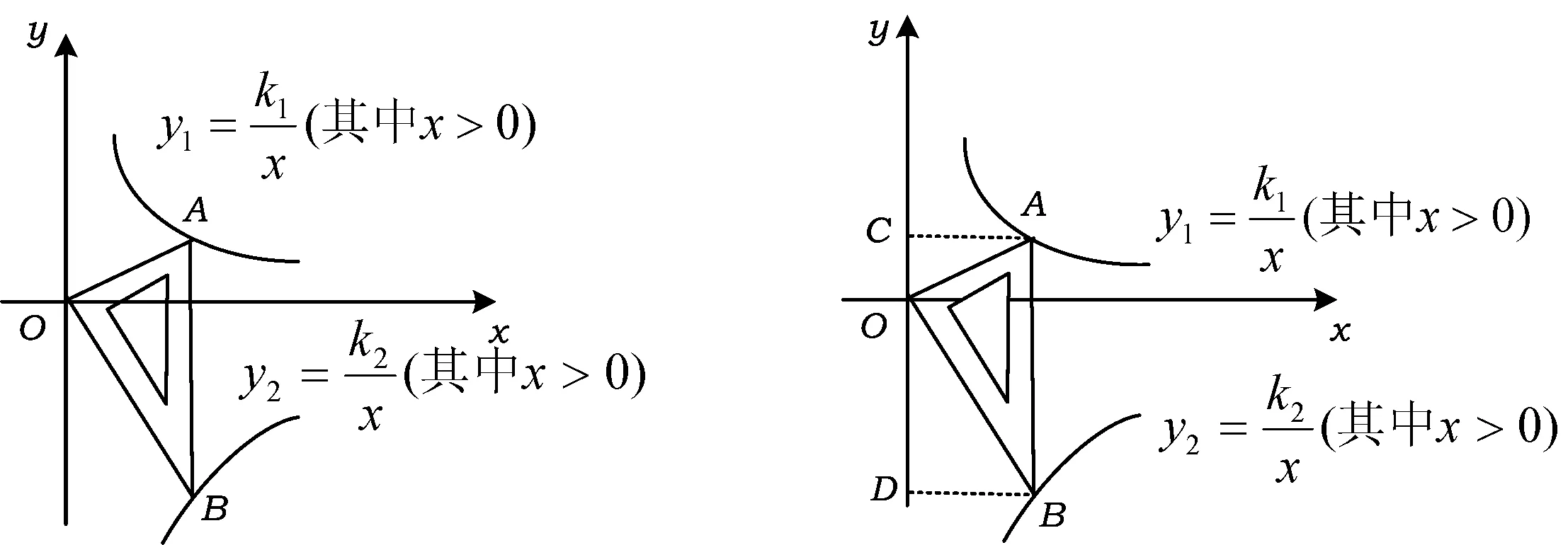
图9 图10
分析如图10,由于∠AOB=90°,因此过点A,B分别作y轴的垂线,垂足分别为点C,D.由“一线三等角”模型可得△ACO∽△ODB,则
而k1=2S△ACO,k2=-2S△ODB,于是
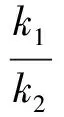
事实上,该题亦可利用异侧型“一线三等角”(如图9,设AB交x轴于点E,则△AOE∽△OBE)求解,由于与上面的解法类似,这里不再赘述.
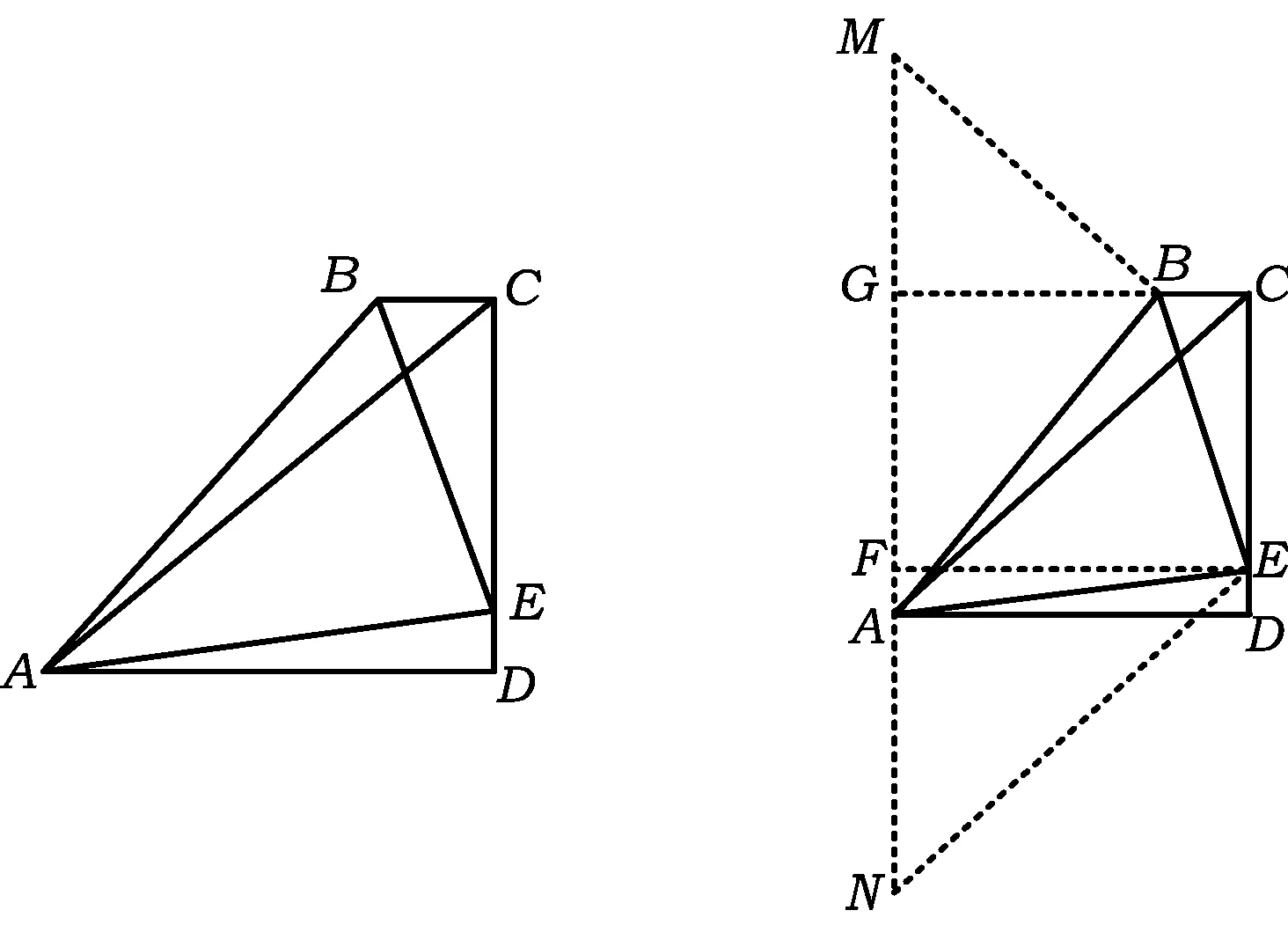
图11 图12
例6如图11,在四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为
( )
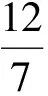
(2017年湖北省鄂州市数学中考试题第10题)
分析如图12,由于∠BAE=45°,因此过点A作AD的垂线,在该垂线上分别找点M,N(其中点N在点A下方),使得∠BMA=∠ENA=45°.过点E作MN的垂线,垂足为点F,延长CB交MN于点G.易知四边形ADCG为正方形,则
AG=CG=CD=4.
而AB=BC+AD,不难推知
AB=5,BG=3,BC=1.
由于∠BAE=∠M=∠N=45°,根据“一线三等角”模型可得△ABM∽△EAN,则
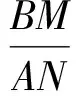
即
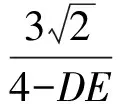
解得
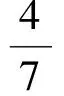
于是
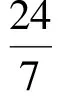
故
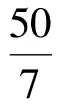
评注上述两道题虽呈现的背景不同,但都蕴知识技能、思想方法、数学模型于图形之中.题中的“特殊角”是解题的关键,也是搭建模型框架的基础,更是学生解题思路的来源与“脚手架”.两道题实质上是考查学生利用模型进行数学思考的能力,同时也有效地检测了学生对数学本质属性的把握情况.
类型4线角齐藏,经验来帮
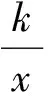
(2017年浙江省金华市数学中考试题第15题)
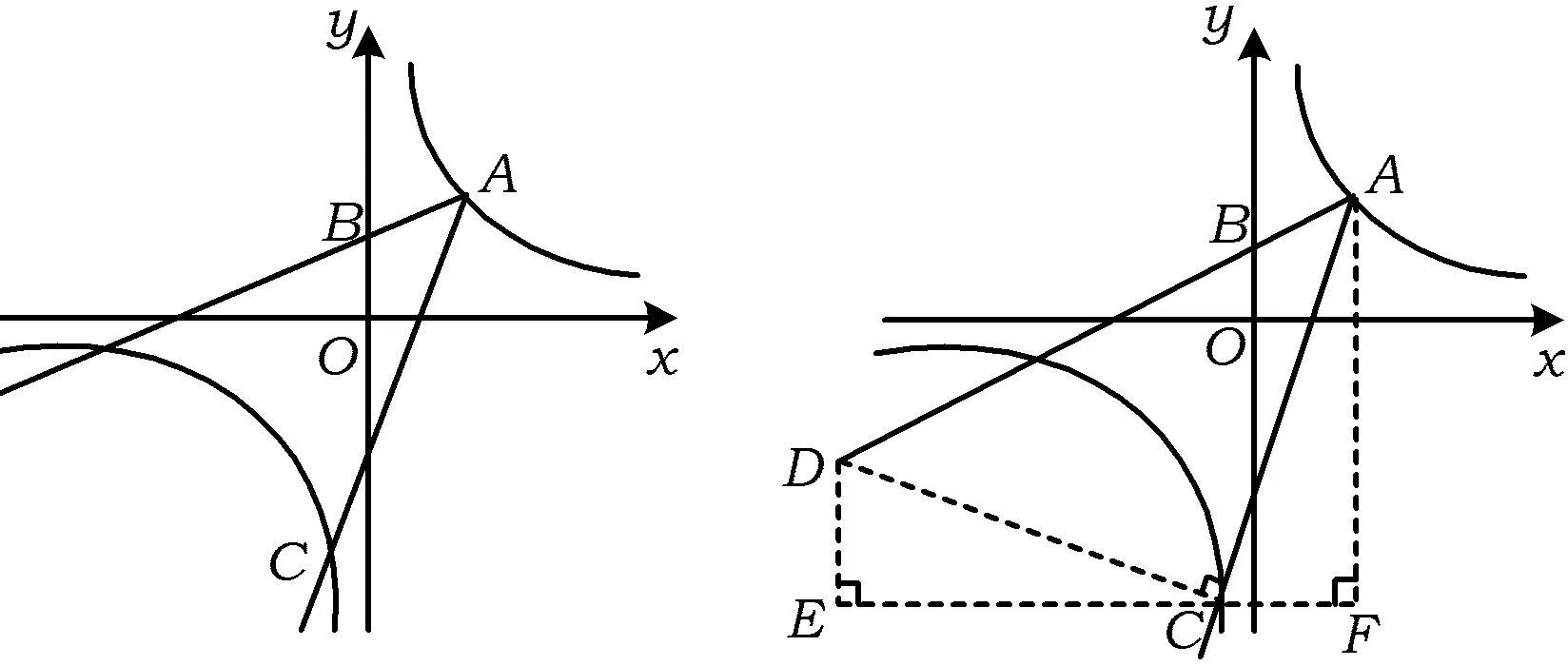
图13 图14
分析如图14,过点C作AC的垂线,交射线AB于点D,过点C作x轴的平行线,在该平行线上分别找点E,F,使得∠DEC=∠AFC=90°.由“一线三等角”模型及∠DAC=45°,得△DEC≌△CFA.又点A,B坐标分别为(2,3),(0,2),从而k=6,于是
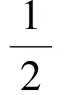
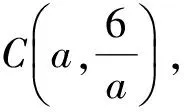
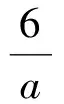
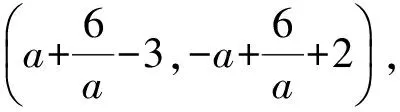
于是
解得a1=-1,a2=2(舍去),故点C的坐标为(-1,-6).
例8如图15,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是______.
(2017年浙江省台州市数学中考试题第16题)
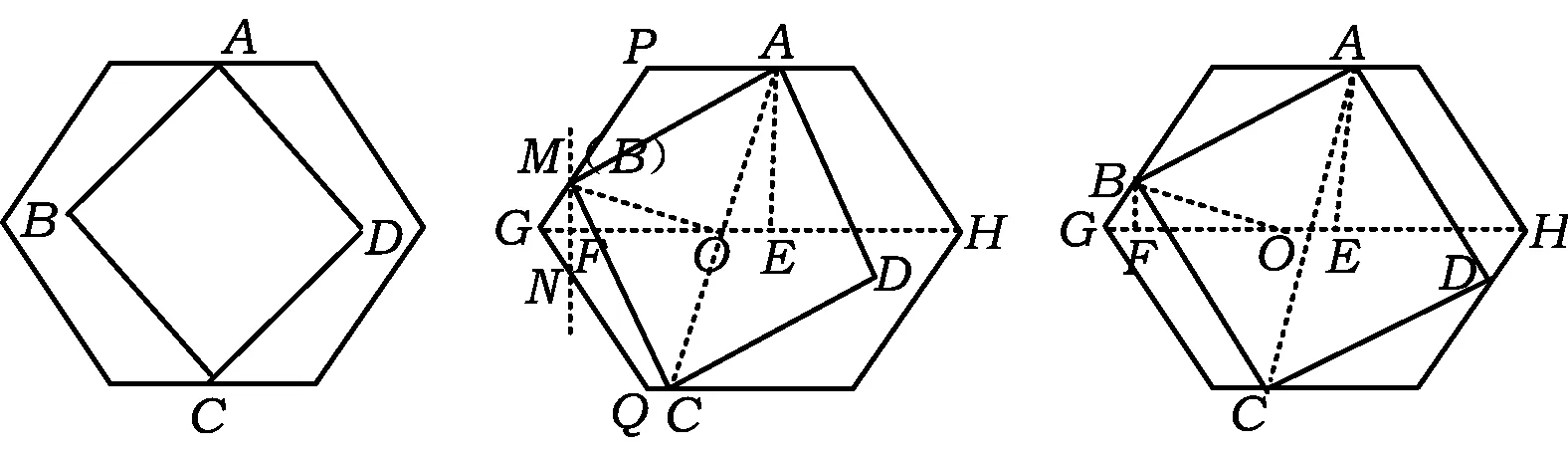
图15 图16 图17
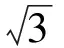

此时

即

故
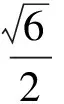
评注上述两道题实质上都以图形的旋转为问题的切入点,能较好地激发学生探索的意愿,促使学生在模拟图形运动的同时,自发地利用题中所蕴含的特殊角,展开适当的联想,寻找图形间的联系,利用数学解题经验,搭建模型框架.两道题都意在寻求突破,体现分层考查,有着较好的考试信度与效度.
通过上述的例3~例8,不难发现:对于有些中考试题,“一线三等角”并非直观、完整地呈现,而是在原图中隐藏了局部或全部结构,因此思维层次随之提升.若我们能充分利用题中所给的已知角或挖掘图中隐藏的特殊角,通过“找角,定线,搭框架”,让模型“现出原形”,则解题思路便会油然而生,豁然开朗.
4 教学启示
在近几年的各地中考试卷中,逐渐涌现出由同一类基本模型延伸而来的试题[1],这些试题虽呈现的背景不尽相同,但解决问题的方法和思想相通,这就要求教师在平时的解题教学中,充分挖掘习题的内在价值,鼓励学生对问题进行深入研究,引导并总结出一般化的方法,同时要让学生尝试利用在解题过程中所积累的经验,对试题中所蕴藏的基本模型进行挖掘与提炼.只有让学生学会自主地反思、推进、提炼,才能做到“掌握模型,举一反三,通一类题”,同时通过对一些基本模型和结论的挖掘,能更好地弄清问题的本质,为解决问题搭建好思维的“脚手架”,进而切实有效地提升学生的解题能力,发展学生的思维水平.当基本模型经过提炼并熟练应用后,教师应引导学生对该模型的变式与拓展进行更深层次地探究,通过让学生在拓展基本模型的过程中,感悟模型的本质,从而做到化题为型、串题成链、结题成网[1],真正实现思维品质的提升.
[1] 姜晓翔.关注“模型教学” 提升“思维品质”[J].中国数学教育:初中版,2017(5):34-36;44.
2017-08-21
胡伟斌(1986-),男,浙江宁波人,中学一级教师.研究方向:数学教育.
O123. 1
A
1003 - 6407(2017)11-13-04

