关注基本模型提炼 拓宽问题解决思路*——以2017年丽水市数学中考第16题为例

●

(温州市第十七中学,浙江 温州 325000)

关注基本模型提炼拓宽问题解决思路*
——以2017年丽水市数学中考第16题为例

●叶茂恒

(温州市第十七中学,浙江 温州 325000)

文章梳理了常见的几何基本模型( 一线三等角型、倍半角模型、12345 型等) ，应用这些模型，并采用多种方法解决了2017 年浙江省丽水市数学中考试题第16 题，呈现解题中基本模型的选择、联想、应用等过程，凸显基本模型与结论在数学解题中的实用价值．

一线三等角型; 倍半角模型; 12345 型

近年来，大量教师在网络上开展解题研究，他们对初中数学实用解题模型较为关注，并注重研究初中数学解题的有效方法，从而实现初中数学解题技能的提升与数学思想方法的有效落地.目前初中阶段数学常用的几何模型有一线三等角型、倍半角模型、12345型等等.这些模型在很多中考问题的解决上有着重要作用，它是分析与解决数学问题的利器.如2017年浙江省丽水市数学中考第16题的第2)小题，应用这些模型可快速找到解题突破口.笔者以此题为例，应用各种模型一题多解.

图1 图2

1 试题呈现

例1如图1，在平面直角坐标系xOy中，直线y=-x+m分别交x轴、y轴于点A，B，已知点C(2，0).

1)略.

2)设点P为线段OB的中点，联结PA，PC，若∠CPA=∠ABO，则m的值是______.

(2017年浙江省丽水市数学中考试题第16题)

模型1一线三等角型[1]

如图2，若∠A=∠DBE=∠C，则△ADB∽△CBE.此模型中，一直线(AC)的同侧有3个相等的角(∠A=∠DBE=∠C)，通常称为一线三等角型，也称为M型相似.当∠A=∠DBE=∠C=90°时，称为三垂直型也称为K型相似，三垂直型是一线三等角型的一种特殊情况.

在图1中直线OB的一侧,若有∠CPA=∠ABO=45°，则可在直线OB的同侧构造一个45°角，即可构造出一线三等角模型.

解法1如图3，在y轴的负半轴上取点E(0，-2)，则可得△OCE为等腰直角三角形，即

∠CPA=∠ABO=∠PEC=45°，

从而

△ABP∽△PEC，

于是

AB∶BP=PE∶CE，

即

解得m=12.

评注一般地，在一直线上已有两个相等的角时，往往可以再添加一等角，构造一线三等角模型求解.在求解过程中，不难证明∠PAB=∠OPC，而△OPC为直角三角形，以∠BAP为锐角构造一个与△OPC相似的直角三角形即可求解.

图3 图4

解法2如图4，过点P作PE⊥AB，垂足为E.由∠BPE=∠CPA=45°,得

∠APE+∠CPO=90°，

又∠APE+∠PAE=90°，从而

∠CPO=∠PAE，

于是

△AEP∽△POC，

可得

AE∶OP=PE∶OC，

即

解得m=12.

评注事实上，由∠CPA=45°往往会联想到构造等腰直角三角形，有了直角三角形进一步会联想到构造三垂直型[2]的一线三等角，这也是在平面直角坐标系中常用的方法.

解法3如图5，过点A作AE⊥PC，垂足为点E，过点E作EF∥x轴，交y轴于点F，过点A作AG⊥EF，垂足为G，则△PAE为等腰直角三角形，且△PFE≌△EGA.设EF=t，则

因为EF+EG=OA=m，所以

OC∶EF=PO∶PF，

即

解得m=12.

类似地，还可以过点C作AP的垂线段构造等腰直角三角形，再构造一线三等角型.

图5 图6

解法4如图6所示作辅助线，则图6中含母子相似三角形(△CEF∽△EAF∽△ACE)、一线三等角型(△CEF∽△EPG)、A型相似(△PAO∽△EAF)等基本图形，从而

△CEF∽△EAF∽△PAO,

于是CF∶EF=EF∶AF=OP∶OA=1∶2，

进而

CF∶AF=1∶4，

即

EF=2CF，AF=4CF.

又因为OF=PG=EF，所以

OC+CF=2CF，

即

CF=OC=2，

故

m=AC+OC=6OC=12.

评注解法3与解法4都是过点C或点A作45°角的另一边的垂线段构造等腰直角三角形.事实上，也可以过点C或点A作45°角上点C或点A所在边的垂线段构造等腰直角三角形，然后构造三垂直型求解.

图7

解法5如图7，过点C作CD⊥PC，交PA于点D，过点D作DE⊥OA，垂足为E，则

△OPC≌△ECD，

从而DE=OC=2，

又因为△DEA∽△POA，所以

DE∶EA=OP∶OA=1∶2，

从而

AE=2DE=4，

于是

解得m=12.

图7

解法6如图8，过点A作AD⊥PA，交PC的延长线于点D，过点D作DE⊥OA，垂足为E，则

△POA≌△AED，

又因为△DCE∽△PCO，所以

OC∶CE=OP∶DE=1∶2，

从而

CE=2OC=4，

于是

m=OA=2OE=12.

模型2倍半角模型

倍半角模型是指两个有公共顶点的有倍角或半角关系，在这种图形模型中存在一些常用的结论或方法.较为常用的是正方形内45°半角模型结论：如图9，在正方形ABCD中，从顶点A出发的45°角的两条射线与边BC，CD分别交于点E，F，联结EF，则BE+DF=EF.简证如下：

图9 图10

如图10，可将△ADF旋转到△ABF′，进而证得△AEF≌△AEF′，于是

EF=EF′=BE+BF′=BE+DF.

解法7如图11，过点P作PE∥x轴交AB于点E，过点E作EF⊥OA，垂足为F，EF交AP于点G.由∠ABO=45°,得

从而四边形PEFO为正方形.由正方形45°半角结论知

EG+OC=CG,

故

解得m=0(舍去)或m=12.

图11 图12

解法8也可如图12所示作辅助线，类似于解法7可列出方程

从而求得m=12.

这种两角之间存在一半或一倍的关系，往往可联想到同弧所对的圆周角与圆心角之间的联系，不妨将45°角看成是某个圆的圆周角，那么此角所对弧所对的圆心角为直角，可利用倍角关系构造出直角三角形，进而结合勾股定理与垂径定理解决问题.

解法9如图13，作AC的中垂线ME交AB于点M，交AC于点E，联结CM，PM，则△CMA为等腰直角三角形.又∠APC=45°，从而点P落在以M为圆心、AM为半径的圆上，于是

PM=CM.

过点M作MF⊥OB，垂足为F，则

MF2+PF2=CM2，

解得m=12.

图13 图14

模型312345型

如图14，在边长为3，4，5的Rt△ABC外构造两个边长为5的等腰△ABE和△ABD，则CE=9，CD=8.设∠D=β，∠E=α，则∠BAC=2β，∠ABC=2α，计算可得

α+β=45°.

整理可得一般性结论如下：

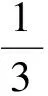
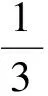
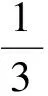
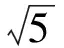
图15

解法10仿解法7做辅助线(如图15)，则

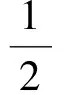
又∠HPI+∠OPC=45°，由12345型相关结论得

即

OP=3OC=6，

从而

解得m=12.

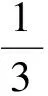
图16 图17

图18 图19

在数学解题中，“如何发现问题的突破口”是很多学生较为困惑的.很多学生在解题时抱着一种盲目心态，而基本模型的提炼学习，可以引导学生从众多的数学问题中寻找到具有共性的模型，这样在提高归纳能力的同时，还能为学生解题提供准确的思考方向和线索.

波利亚在《怎样解题》中提出：在拟订方案时应当回顾是否解过类似的问题，能否将问题转化为已解决的问题[3].由于学生已接触过大量的数学问题，一方面在大脑中的检索过慢，另一方面很多问题没有归纳典型模型，大量信息相互干扰，不利于回顾.在回顾与解题之间增加一个提炼数学模型的过程，可以减少大量数据记忆，在大脑加深典型模型印象，提高回顾检索效率，从而更好地拓展解题思维.

[1] 周礼寅．一线三等角模型的建立与应用[J]．中国数学教育，2012(10)：27-30．

[2] 沈占立．例说与正方形有关的“三垂直”[J]．中学生数理化，2015(6)：23．

[3] 波利亚．怎样解题[M]．涂泓，冯承天，译．上海：上海科技教育出版社，2002．

2017-09-11

叶茂恒(1975-)，男，浙江温州人，中学高级教师.研究方向：数学教育.

O123． 1

A

1003 - 6407(2017)11-09-04