二维完全弹性碰撞的理论研究
周 游 刘 程 涂灿辉 刘 华 郑才龙
(湖北师范大学化学化工学院 湖北 黄石 435002)
二维完全弹性碰撞的理论研究
周 游 刘 程 涂灿辉 刘 华 郑才龙*
(湖北师范大学化学化工学院 湖北 黄石 435002)
用相关的物理知识解决二维碰撞的问题,发现碰撞中更为普遍的规律.对于二维完全弹性碰撞问题,可以用矢量分解、能量守恒和动量守恒解决.
二维弹性碰撞 矢量分解 能量守恒 动量守恒 速度
在生活或学习中,有许多的碰撞现象,例如桌球之间的碰撞、微观粒子之间的轰击、天体之间的相互撞击等.这些过程有明显的特点:一般发生在二维平面内,相互作用的时间极短,相互作用力极大,运动状态瞬间发生急剧改变,在物理学中这类问题叫做碰撞[1~3].
碰撞是生活中常见的现象,也是经典物理学的重点,更是动量中的核心内容.最初动量守恒定律正是为了解决碰撞问题而发现的.我们在中学物理中学习了对心碰撞,领悟到动量的巨大魅力.
通常所说的碰撞包括正碰和斜碰,本次研究较为复杂且应用更广的斜碰,即二维碰撞.发生斜碰的两个物体光滑,没有摩擦,碰后两物体只有平动没有转动,这是完全弹性二维碰撞的条件.如果系统有摩擦,则碰后物体既有平动又有转动,且有能量损失,属于普通二维碰撞,此问题难以解决[4~6].
关于二维碰撞问题,不少学者对其进行理论或实验的研究,如用质心系法、矢量三角形、计算机程序、碰撞实验等方法进行研究;基于他们的工作,我们用基础物理学知识系统地研究了二维完全弹性碰撞[7,8].本文介绍了用通俗易懂的物理方法解决较为复杂的问题,得到了速度大小和方向的准确解析解,对各种碰撞情况进行分类讨论,并通过作图辅助说明均得到了相应的结论,从而拓展了碰撞研究的广度和深度.
从简单情况出发,处理两个小球的二维完全弹性碰撞.设质量为m1的小球A以初速度v0射向质量为m2静止的小球B,如图1所示,初速度v0方向和两球碰撞时球心连线方向所成的入射夹角为α(0≤α<90°),发生弹性碰撞后,求解末速度大小和散射角.

图1 二维完全弹性碰撞分析图
1 解决思路
由于两球碰撞为理想的二维碰撞,故碰撞过程能量守恒、动量守恒.A和B碰撞瞬间如图1状态.以两球球心连线方向为x轴,垂直于球心连线且过A球心的方向为y轴;可以设A的末速度v1沿x轴方向分量为vx,在y轴方向上分量为vy,故与B发生作用的只有vx,根据一维碰撞规律,B碰后末速度方向必然和vx方向共线.在任意两个正交方向上运用分动量守恒,并结合能量守恒和分速度关系,即可求解末速度.
2 解决过程
设A碰后的末速度大小为v1,B碰后的末速度大小为v2,v1在x和y轴方向的分量分别为vx和vy,A碰后v1与碰前v0方向夹角为β,碰后两球末速度v1和v2之间的夹角为θ,即有角度关 系α+β=θ.
若引入恢复系数

本次研究情形即e=1,可用于求解检验.
由x轴方向分动量守恒有
m1v0cosα=m1vx+m2v2
(1)
由y轴方向分动量守恒有
m1v0sinα=m1vy
(2)
由系统碰撞前后能量守恒有
(3)
由v1的合、分速度关系有
(4)
由式(1)~(4)即可求解.
由式(1)得

由式(2)得
vy=v0sinα
将vx和vy代入到式(4)有
化简得
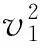
化简得

因
将v2代入上式有
化简得
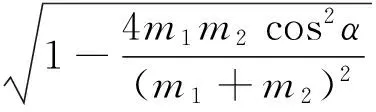
或

因为动量在v0方向上守恒,故
m1v0=m1v1cosβ+m2v2cosα
将v1和v2代入上式得
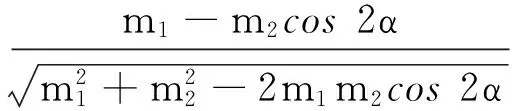
又因为

联立并将v1和v2代入得

3 分析讨论
二维弹性碰撞的两球末速度大小为
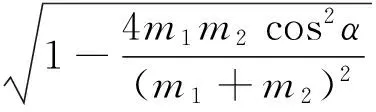

A的末速度v1与v0方向夹角为
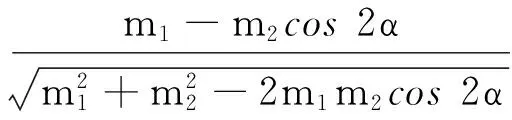
两球末速度方向夹角为

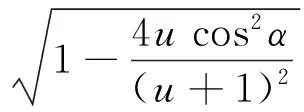

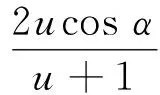

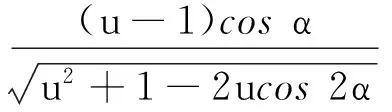
特别地,可以分下列几类情况讨论:
(1)当两球质量相等时,即u=1时,公式可以简化为
v1=v0sinαv2=v0cosα
β=90°-αθ=90°
(2)当碰前夹角α=0,碰撞前后速度始终共线,变为一维弹性碰撞,即弹性正碰情形


β=θ=0
(3)当m1>m2,两球末速度夹角为锐角;
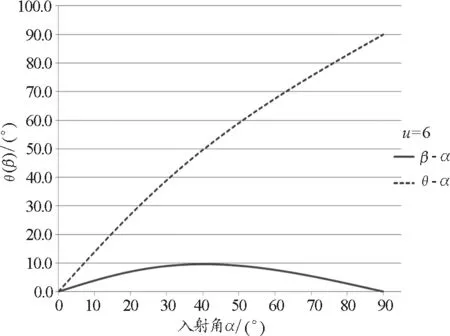
当m1 当m1=m2,两球末速度夹角为直角. (4)当m1≫m2,即u很大时 v1≈v0v2≈2v0cosα β≈0θ≈α 当m1≪m2,即u≈0时 v1≈v0v2≈0 β≈180°-2αθ≈180°-α (1)v1和v2随α变化图像 1)当u=0.5时,v1和v2随α变化图像如图2所示. 图2 u=0.5时,v1和v2随α变化图像 2)当u=1时,v1和v2随α变化图像如图3所示. 图3 u=1时,v1和v2随α变化图像 3)当u=2时,v1和v2随α变化图像如图4所示. 图4 u=2时,v1和v2随α变化图像 小结:无论质量比如何变化,v1随α改变而递增至v0,v1随α改变而递减至零. (2)β和θ随α变化图像 1)当u=0.1时,β和θ随α变化图像如图5所示. 图5 u=0.1时,β和θ随α变化图像 2)当u=2时,β和θ随α变化图像如图6所示. 图6 u=2时,β和θ随α变化图像 3)当u=6时,β和θ随α变化图像如图7所示. 图7 u=6时,β和θ随α变化图像 小结:当u≤0.3时,β和θ随α变化的图像接近递减的直线,θ在两端点取值为180°和90°;β在两端取值为180°和0;且u越小,拟合度越高. 当u≥6时,θ随α变化的图像接近递增的直线,且u越大,拟合度越好;而β有极大值,且β在两端点均为零,u越大β的极大值越小. 鉴于当质量比u>1时,在入-散射角图像中发现A的散射角度β有极大值,通过求导,即 得 ucos 2α=1 即β在 处有 在上述图像中,将质量比代入极值公式 u=2α=30.00°βmax=30.00° u=6α=40.20°βmax=9.59° 本文从理论上严谨地推导了二维完全弹性碰撞的速度公式,并对其进行深入地分析讨论.通过一维碰撞等特殊情况的验证,以及图像的直观变化规律,我们对较为陌生的斜碰有了更为完整的认识和深刻的理解.本文解决了中学尚未学习而大学忽略讨论的斜碰问题,发现了斜碰的力学规律,拓展了经典力学研究碰撞的范围. 1 陈亚兰.一维对心完全弹性碰撞的速度分析.河南科技,2014(01):184~184 2 朱晓波,黄奚超,邹毅.二维碰撞的简化计算及其电脑程序.吉林工业大学自然科学,2001(31):91~95 3 曾奇军,戈静,徐元国,等.弹性碰撞的图示分析法.信阳师范学院学报(自然科学版),2013,26(3):343~347 4 人民教育出版社.高中物理选3-5.北京:人民教育出版社,2010 5 漆安慎,杜婵英.力学(第3版).北京:高等教育出版社,2012 6 H.Orland,R.Schaeffer.Two-body collisions and time dependent Hartree-Fock theory.Zeitschrift für Physik A:Atoms and Nuclei,1979,290(2):191~204 7 李忠相.处理斜碰问题的三种方法.物理通报,2014(5):35~37 8 刘金铭,陈阳,陈琪.关于弹性斜碰前后系统动能的讨论.湖南中学物理,2015(2):82~84 TheTheoreticalResearchonTwo-dimensionalPerfectElasticCollision Zhou You Liu Cheng Tu Canhui Liu Hua Zheng Cailong (School of Chemistry and Chemical Engineering,HuBei Normal University,Huangshi,Hubei 435002) The Collision is a common phenomenon in our life,and it is important for classical physics,as well as it is the core content in the momentum.The first law of conservation momentum was found in order to solve the problem of collision.We have learnt the central collision in the high school and comprehended the great charm of momentum.In this article,we use the relevant physical knowledge to solve the two-dimensional collision problem,and find the more general regular in collision.As for the problem of two-dimensional perfect elastic collision,the vector decomposition,energy conservation and momentum conservation can be used to solve it. two-dimensional elastic collision; vector decomposition; energy conservation;conservation of momentum;speed 2017-03-23) *指导教师:郑才龙(1971- ),男,讲师,主要从事物理教学工作.4 图像解析







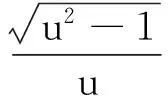
5 研究总结
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

