例谈运动学图像的妙用①*
何崇荣
(武汉市黄陂区第一中学 湖北 武汉 430300)
张 黎
(武汉市黄陂区第三中学 湖北 武汉 430317)

例谈运动学图像的妙用①*
何崇荣
(武汉市黄陂区第一中学 湖北 武汉 430300)
张 黎
(武汉市黄陂区第三中学 湖北 武汉 430317)
举例介绍利用图像法巧妙解决一些比较复杂的运动学问题.
运动学 图像 妙用
图像法是解决物理问题常用的方法,它往往能直观地反映物理规律.利用图像法解题有时能将复杂问题简单化,形成巧解.下面通过具体例子来谈谈运动学图像的巧妙应用.
1 速率-时间图像
【例1】如图1所示,一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC,已知AB和AC的长度相等.两个小球p和q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面的先后( )
A.q小球先到 B.p小球先到
C.两小球同时到 D.无法确定

图1 例1题图
答案:A.
解析:小球p沿光滑斜面做匀加速直线运动,小球q沿光滑曲面下滑,沿曲面切线方向的加速度不断减小.根据机械能守恒,两小球到达水平面的速率相同.于是画出两者运动的速率-时间图像如图2所示,图像直观表明:tq

图2 速率-时间图像1

图3 速率-时间图像2
评析:要比较两小球到达水平面的时间,可以考虑将两者到达水平面的时间表示出来.但是小球q沿光滑曲面下滑,做一般的曲线运动,很难表示小球q到达水平面的时间.而利用速率-时间图像,不用求两者到达水平面的时间表达式,就能直观反映两者所用时间大小关系.
2 速度-时间图像
【例2】(原创题)机车启动往往有两种方式:以恒定功率(即额定功率)启动和以恒定的加速度启动,设机车分别按这两种方式从静止启动到获得最大速度所用时间分别为t1,t2,行驶距离分别是s1,s2,则关于机车两种启动方式所用时间及行驶距离比较正确的是( )
A.t1>t2B.t1 C.s1 答案:B,C. 解析:如图4所示,是机车启动过程的速度-时间图像.曲线OBC表示以恒定功率启动,曲线OAD表示以恒定加速度启动.设机车从静止启动,获得的最大速度为vm,机车以恒定的加速度启动,匀加速持续的时间为t0,此时机车的速度为v1m,机车的额定功率为Pm,曲线上A,B两点对应的牵引力分别为FA,FB,两点的加速度分别为aA,aB. 图4 机车启动的速度-时间图像 在A点有 Pm=FAv1m 在B点有 Pm=FBv1m 于是FA=FB,根据牛顿第二定律得 aA=aB 所以曲线BC与曲线AD完全相同,所以t1 由于曲线BC与曲线AD完全相同,所以曲线BC与坐标轴围成的面积和曲线AD与坐标轴围成的面积相同.对于曲线OBC,设曲线上B点的切线与t轴相交于E点,则OA//BE,于是△BB′E≅△AA′O,所以曲线OB与坐标轴围成的面积小于直线OA与坐标轴围成的面积.所以s1 评析:机车不管采用哪种方式启动,运动过程中都有一阶段做的是变加速直线运动,那么很难定量表示机车行驶时间和距离.但利用速度-时间图像可直观反映两种启动方式中所用时间的大小关系以及行驶距离间的大小关系. 【例3】在地面上以初速度2v0竖直上抛一物体A后,又以初速度v0在同一地点竖直上抛另一个物体B,若要使两物体能在空中相遇,则两物体抛出的时间间隔Δt必须满足的条件是(不计空气阻力)( ) 答案:C. 解法1:找出临界情况 当时间间隔Δt较小时,会导致B已落地,A还在空中,所以最短时间间隔为B落地时,A也恰好落回原处相遇,因此 当时间间隔Δt较大时,会出现A已落地,B还没有抛出,所以最长时间间隔为B抛出时,A也恰好落回原处相遇,因此 所以要使两物体能在空中相遇,两物体抛出的时间间隔Δt必须满足 解法2:根据运动学知识列方程求解 设B抛出后经过时间t,两者在空中相遇.则 然后根据xA=xB,B在空中运动的时间t满足 解法3:利用位移-时间图像求解 两物体的位移-时间图像,如图5所示,两条图线的交点表示A,B相遇时刻,由图可直观看出两物体抛出的时间间隔Δt必须满足 图5 位移-时间图像 拓展:当两物体抛出的时间间隔Δt必须满足什么条件时,B在上升(或下降)阶段与A相遇呢? 图像很直观地显示B刚好到达最高点时与A相遇这种临界情况. 设B刚好到达最高点时与A相遇,根据xA=xB得 解得 于是当 时,B在下降阶段与A相遇;当 时,B在上升阶段与A相遇. 评析:第一种解法两种临界情况不是那么容易判断出来;第二种解法利用运动学知识列方程计算比较麻烦;第三种利用位移-时间图像求解就很直观明了,借助图像可以很容易理解两种临界情况,也能直观显示两物体相遇具体情景. 【例4】(改编题)如图6所示,把一重为G的物体,用水平推力F=kt(k为恒量,t为时间)压在竖直的足够高的平整墙上,从t=0开始,求物体运动的时间和最大速度. 解析:分析物体的运动情况,对物体,根据牛顿第二定律有 mg-μN=ma N=F=kt 所以 mg-μkt=ma 物体先做加速度逐渐减小的加速运动,当加速度减为零时 之后正压力N继续增大,则摩擦力继续增大,于是物体开始减速,减速阶段加速度大小 所以第二阶段物体做加速度逐渐增大的减速运动,当物体速度减为零时,物体静止. 图6 例4题图 这两个阶段,物体的加速度关于t=t1对称,如图7所示,于是全过程物体的运动时间 由于物体加速度a与时间t满足线性关系,于是a-t图像与坐标轴围成的面积很容易计算,从而求出物体的最大速度 Δv=Sa-t=vm-0 则 图7 加速度-时间图像 评析:由于物体做的是变加速直线运动,高中阶段不可能用运动学公式求解.而物体加速度a与时间t满足线性关系,于是可以利用a-t图像求解物体运动的最大速度和时间. 2017-03-14) *①《物理通报》武汉工作室供稿.
3 位移-时间图像










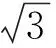


4 加速度-时间图像