关于特征值及特征向量的教学分析

(盐城工学院 数理学院，江苏 盐城 224003)

关于特征值及特征向量的教学分析

卞小霞

(盐城工学院 数理学院，江苏 盐城 224003)

工程技术及科学研究中的很多问题常可归结为求矩阵的特征值、特征向量的问题，结合教学实践探讨如何引起学生的学习兴趣，如何讲解概念、性质并进行延伸分析。

特征值；特征向量；矩阵；应用

特征值和特征向量是重要的代数概念，在经济、工程、基础研究等领域都有广泛的应用。例如，特征值的符号可以确定一类工程系统的稳定性，可以判断特定经济模型的有效性等，而判断依据特征值、特征向量的概念比较抽象，其概念及性质适合引导学生自主发现、探索，有利于培养学生的分析能力和创新能力。国内不少高等代数教材及线性代数教材[1-3]都以行列式为工具介绍特征值理论，文献[4-5]介绍了特征值理论的非行列式观点。本文在已有理论的基础上，结合学校线性代数作为工科学生公共基础课的教学实践，分析了更为合理的特征值、特征向量的教学设计。

一、创设情境、激发兴趣

通过现实生活中的例子说明教学内容的重要性，比如，桥梁坍塌的实例。塔科马海峡大桥于1940年建成，位于美国华盛顿州，而同年11月7日，在19 m/s的低风速下因颤振而破坏，此消息震惊了世界，也引起了科学家们对振动问题的研究，正是他们的研究为后人减少了很多不必要的灾害。

在振动问题的研究中，很多数学模型为常微分方程，常微分方程是在高等数学中已经学过的知识点，我们学习了各种求解方法，但仍有很多方程较难求解，此时，方程的稳定性可以不需要求出具体解，而只通过一阶项系数矩阵的特征值来判断。

比如某实际问题的数学模型为：

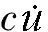
(1)

为了分析其平衡点的稳定性，首先将方程改写成：

(2)

其派生系统为：

(3)

该系统有唯一的平衡点(0，0)，对于派生系统(3)，系数矩阵的特征值有一个为正值，则(0，0)是不稳定的鞍点，由Lyapunov稳定性定理[6]知原系统(1)在(0，0)处也是不稳定的，那么对于这个实际问题，需要修正它的结构参数才能使其稳定。

在上述问题分析过程中，避开了求解较复杂的常微分方程，只是利用系数矩阵的特征值进行了判断。什么是特征值？如何求解矩阵的特征值呢？

二、概念剖析、性质初探

定义[2]：设A是n阶矩阵，如果数λ和n维非零列向量x使关系式

Ax=λx

(4)

成立，那么，这样的数λ称为方阵A的特征值，非零向量x称为A的对应于特征值λ的特征向量。

学生在高等数学中利用λ作为拉格朗日乘数求极值问题。此处，若是求满足约束xTx=k时xTAx的极值，则构造拉格朗日函数L=xTAx-λ(xTx-k)，令▽L=2Ax-2λx=0，得到Ax=λx时，可取得xTAx的极值。可见极值问题中，λ正是特征值的定义，这是从表达式的角度直接诠释了特征值的意义。

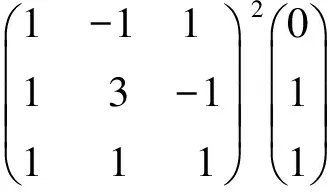
由例1的结果，学生会提出问题：

2.对于一般的n阶方阵A，x≠0，λ∈R，若Ax=λx，则Anx=λnx吗？

3.定义中的λ，x怎么求？

这三个问题的讨论也是对特征值性质的分析。

三、问题追踪、归纳方法

对于问题1，结合例1中已做的计算，再由n=k的假设，可得n=k+1的结论，根据数学归纳法，得到问题1的回答是肯定的；对于问题2，k=1时，Ax=λx，设k=n时，Anx=λnx，则k=n+1时，

An+1x=A(Anx)=A(λnx)=

λn(Ax)=λnλx=λn+1x

故问题2的回答也是肯定的。

对于问题3，要使Ax=λx有非零解x，即(A-λI)x=0有非零解，由齐次方程组有非零解的充要条件是|A-λI|=0，解得特征值λ，代入(A-λI)x=0，得到解x为对应的特征向量。

由以上分析归纳得到求解方阵的特征值、特征向量的一般方法：

(1)称|A-λI|=0为特征方程，此方程为一元高次方程，求解得到所有的特征根λ1，λ2…λn；

(2)对每一个λi求出方程(A-λiI)x=0的基础解系，相应的通解即为对应于λi的全部特征向量。

四、例题讲解、性质总结

例2：求出下列方阵的全部特征值和特征向量。

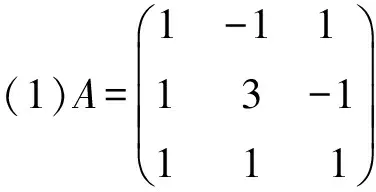
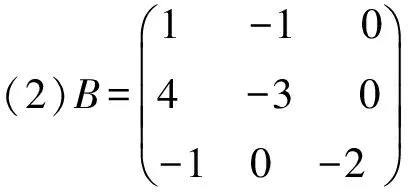
这两个小例题介绍的特征值与特征向量对应情况由浅入深，(1)(2)的特征值都有重根，(2)中重根对应的线性无关的特征向量个数小于重根数，为引入性质奠定基础，考虑其实际意义，矩阵(1)对应的系统在平衡点(0，0，0)处不稳定；矩阵(2)对应的系统在平衡点(0，0，0)处渐进稳定。

讲解完例2，介绍以下性质：

性质1：若λ是方阵A的特征值，则λk是方阵Ak的一个特征值，k∈N；

性质2：方阵A的属于不同特征值的特征向量是线性无关的；

性质3：任一特征值的代数重数不小于它的几何重数。

性质1由前面例1总结可得，性质2由线性无关的定义容易证得，而性质3可由学生课后讨论总结。

五、扩展应用、延伸分析

由矩阵的特征值，可以容易得到矩阵行列式的值、迹、惯性、是否可逆、能否对角化等，此外，也可得到矩阵多项式的特征值、逆等，这些延伸性的应用大多是在实际工程技术、科学研究中的收获。为了让学生体会到这一点，有必要作如下学习要求：

1.了解特征值、特征向量在工程技术领域的应用情况，学生通过查阅相关资料，总结出应用报告；

2.本节课介绍了利用行列式的方法求得特征值，请学生尝试用其他的方法求得特征值[3-4]；

3.课堂上没有严格证明的性质，请学生补充证明过程。

六、结论

本节课设计由生动的引例引出了特征值、特征向量的概念，认识了特征值和特征向量能解决的问题，通过方程分析找到了求特征值、特征向量的一般方法，归纳了特征值与特征向量的性质。

特征值及特征向量的概念本身具有实际的背景意义，相关内容丰富，应用广泛，研究的方法多样，与学生一起探讨分析有利于他们研究能力、创新能力的培养。

[1]北京大学数学系几何与代数教研室代数小组.高等代数(第二版)[M].北京：高等教育出版社，2003.

[2]同济大学数学系.工程数学线性代数[M].北京：高等教育出版社，1990.

[3]陈万勇，等.线性代数[M].北京：电子工业出版社，2013.

[4]邓勇.关于矩阵特征值理论的教学新设计[J].数学教育学报，2015，24(6)：44—46.

[5]钟凤远，王树忠，葛斌.矩阵初等变换的应用[J].哈尔滨师范大学自然科学学报，2016，32(1)：19—21.

[6]胡海岩.应用非线性动力学[M].北京：航空工业出版社，2001.

AnalysisonEigenvaluesandandEigenvectorofMatrixTeaching

BIAN Xiao-xia

(School of Mathematics and Physics, Yancheng Institute of Technology, Yancheng 224003, China)

Many problems in science and technology research projects often can be attributed to the eigenvalues and eigenvector of matrix. The paper explores how to arouse students’ interest in learning, how to explain the concept, nature and make an extension analysis combined with the teaching practice .

eigenvalue; eigenvector; matrix; application

10.3969/j.issn.1008-6714.2017.11.028

O172.1

A

1008-6714(2017)11-0068-03

2017-07-12

卞小霞(1984— )，女，江苏盐城人，讲师，博士研究生，从事一般拓扑学研究。

〔责任编辑：李海波〕