三维Lotka-Volterra系统的全局扇形稳定性

周 武, 陆征一

(1. 西南民族大学 计算机科学与技术学院, 四川 成都 610041; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

三维Lotka-Volterra系统的全局扇形稳定性

周 武1, 陆征一2

(1. 西南民族大学 计算机科学与技术学院, 四川 成都 610041; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

将Volterra-Lyapunov矩阵稳定性蕴含全局扇形稳定的结论推广到三维情形,得到了Volterra-Lyapunov矩阵半稳定性蕴含全局扇形稳定.

Volterra-Volterra半稳定; 边界平衡点; 全局稳定性

考虑如下Lotka-Volterra系统

(1)

关于此系统正平衡点的存在性及其全局稳定性,特别是在相互作用矩阵A=(aij)n×n的Volterra-Lyapunov稳定性和平衡点的局部稳定下,对于链型系统[1-4]、环形系统[4-5]和一般系统[1,6-7]的全局稳定性研究已经有很多结果,这些问题的解决最终都化为LaSalle不变集的确定,一旦其LaSalle不变集得到确定[1,7],就可得到系统的全局动力学行为.

本文利用Volterra-Lyapunov函数,将边界平衡点的稳定性问题化为系统对应的LaSalle不变集的确定问题,通过分析其LaSalle不变集的结构,得到系统的全局扇形稳定性.

考虑三维系统

(2)

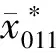
为了讨论扇形稳定性,本文给出几个相互作用矩阵的稳定性概念.

定义2[7]矩阵A称为是Volterra-Lyapunov稳定的,如果存在正对角矩阵C,使得CA+ATC负定.

定义3[1]矩阵A称为是Volterra-Lyapunov半稳定的,如果存在正对角矩阵C,使得CA+ATC半负定.

对于Lotka-Volterra系统正平衡点的全局稳定性来说,相互作用矩阵A为Volterra-Lyapunov稳定是充分的[1,6-7].而A为Volterra-Lyapunov半稳定是不够的,还需要矩阵的结构或平衡点的局部渐进稳定性作为附加条件[3,7].

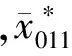
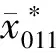
例1

(3)

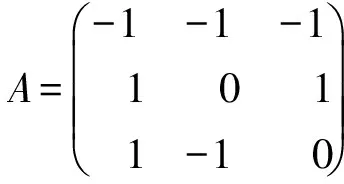
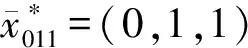
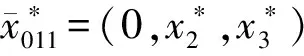
1 主要结果

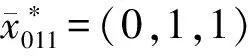
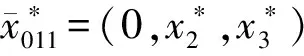
(4)

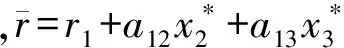
又因为A为Volterra-Lyapunov半稳定的,故存在正对角矩阵C=diag(c1,c2,c3),使得Volterra-Lyapunov函数

V(x)=c1x1+c2(x2-lnx2)+c3(x3-lnx3)

满足

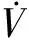
(5)

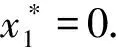
(6)

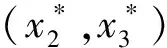
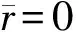
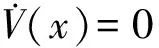
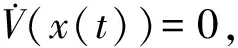
(7)

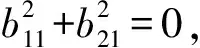
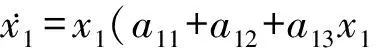
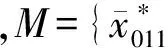
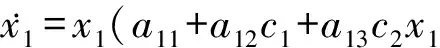
(8)

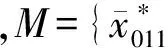
情况3当秩(B)=1时,不妨设

当b12=b13=0时,x1=0,故有

(9)

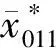
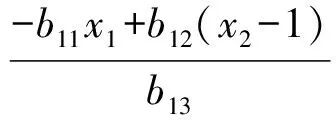
代入(4)式有

(10)

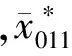
综上,定理得证.

[1] 陈兰荪,宋新宇,陆征一. 数学生态学模型与研究方法[M]. 成都：四川科学技术出版社，2003.

[2] GÜRLEBECK K, JI X. Lotka-Voterra system with Volterra multiplier[C]//ARABNIA R H, TRAN Q N. Software Tools and Algorithms for Biological Systems. New York:Springer-Verlag,2011:647-655.

[3] LIU L, LU Z Y, WANG D M. The structure of LaSalle’s invariant set for Lotka-Volterra systems[J]. Science in China:Math,1991,A34(7):783-790.

[4] LU G, LU Z. Geometric approach for global asymptotic stability of three-dimensional Lotka-Volterra systems[J]. J Math Anal Appl,2012,389(1):591-596.

[5] 彭芬国,周之铭. 环状三维捕食-被捕食Volterra系统的全局渐近稳定性[J]. 生物数学学报,1988,3(2):159-170.

[6] GOH B S. Global stability in many-species systems[J]. The American Naturalist,1977,111(977):135-143.

[7] HOFBAUER J, SIGMUND K. Evolutionary Games and Population Dynamics[M]. Cambridge:Cambridge University Press,1998.

[8] TAKEUCHI Y. Global Dynamical Properties of Lotka-Volterra Systems[M]. Singapore:World Scientific,1996.

[9] REDHEFFER R. A new class of Volterra differential equations for which the solutions are globally asymptotically stable[J]. J Diff Eqns,1989,82(2):251-268.

[10] SOLIMAN A A, AL-JARALLAH E S. Asymptotic stability of solutions of Lotka-Volterra predator-prey model for four species[J]. Appl Math,2015,6(4):684-693.

Global Sector Stability for Three-dimensional Lotka-Volterra Systems

ZHOU Wu1, LU Zhengyi2

(1.SchoolofComputerScienceandTechnology,SouthwestUniversityforNationalities,Chengdu610041,Sichuan;2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

The global stability for a positive equilibrium of a three-species Lotka-Volterra system is generalized to the global stability for a nonnegative equilibrium under the Volterra-Lyapunov stability for the interaction matrix of the system.

Volterra-Volterra semistability; boundary equilibrium; global stability

2016-08-30

高等学校博士学科点专项科研基金(20115134110001)

周 武(1962—),男,副教授,主要从事运筹学与控制论及微分方程的研究,E-mail:744971475@qq.com

O193

A

1001-8395(2017)05-0606-03

10.3969/j.issn.1001-8395.2017.05.007

2010MSC:34D05

(编辑 周 俊)