Cn-内射模及其刻画

王 茜, 王芳贵, 何 可

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

Cn-内射模及其刻画

王 茜, 王芳贵*, 何 可

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

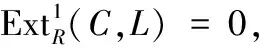
n-余挠模; Cn-内射模; Artin半单环; CnI-遗传环

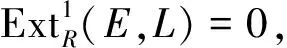
1959年,D. K. Harrison[5]为了刻画非有限的Abelian群的结构性质,开展了余挠模的研究(如文献[6-7]).左R-模C称为余挠模,是指对一切平坦模F,都有

2006年,Mao L. X.等[8]引入了n-余挠模概念,左R-模C称为n-余挠模,是指对一切平坦模F,都有

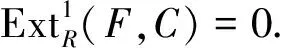
本文借助n-余挠模类引入了Cn-内射模的概念,并讨论其相关性质和等价刻画,证明了L是内射模当且仅当L是n-余挠维数不超过1的Cn-内射模.借助于Cn-内射模的概念,给出了Artin半单环和弱整体维数不超过n的环的新刻画.证明了每个R模都是Cn-内射模的环就是Artin半单环,每个n-余挠模是Cn-内射模的环就是弱整体维数不超过n的环;从而有每个余挠模是C-内射模的环就是von Neumann正则环,1-余挠模是C1-内射模的整环就是Prüfer整环.最后用Cn-内射模的商模是Cn-内射模定义了CnI-遗传环并得出了其等价刻画和一些性质,即R是CnI-遗传环当且仅当R上每个n-余挠模的投射维数不超过1.

以下恒设R是有单位元的结合环,n是非负整数,模指左模.用F、P和I分别表示平坦模类、投射模类和内射模类,Fn和Cn分别表示平坦维数不超过n的模类和n-余挠模类.另外,pdRM与idRM分别表示R-模M的投射维数和内射维数,w.gl.dim(R)表示环R的弱整体维数,其他涉及到的符号可以在文献[14]中找到.

1 Cn-内射模定义和基本性质

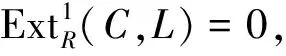
注1.2下面的事实是显然的.

1) 内射模是Cn-内射模.

2) 若m≥n≥0,则CnI⊆CmI,即Cn-内射模是Cm-内射模.

3) 由于I⊆Cn,故CnI⊆CPI,即Cn-内射模是余纯内射模.

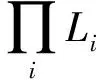
证明由自然同构

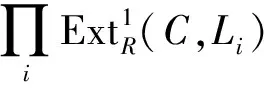
即得.

命题1.4设0→X→Y→Z→0是正合列.若X、Z是Cn-内射模,则Y也是Cn-内射模.

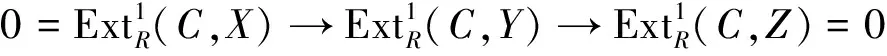
设L是一个模类.设M∈L,X是R-模,φ:M→X是同态.若对任何N∈L,以及任何同态g:N→X,恒有同态h:N→M,使下图

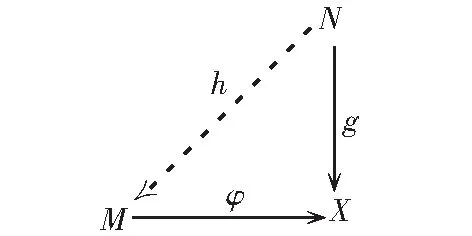
完备为交换图,则(M,φ)称为X的L-预盖.显然,φ:M→X是L-预盖当且仅当对任何N∈L,诱导同态

φ*:HomR(N,M)→HomR(N,X)

是满同态.

定理1.5对R-模L，以下各条等价:

1)L是Cn-内射模;

2) 若ξ:0→L→C→Z→0是正合列,其中C∈Cn,则C→Z是Z的Cn-预盖;

3)L是某个Cn-满预盖φ:A→B的核,其中A是内射模;

4) 若ξ:0→A→B→C→0是正合列,其中C∈Cn,则HomR(ξ,L)也是正合列;

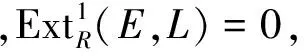
2)⟹3)L能嵌入内射模E,注意E∈Cn.取A=E,B=E/L.由条件,L是Cn-满预盖φ:A→B的核.

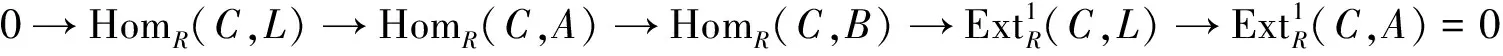
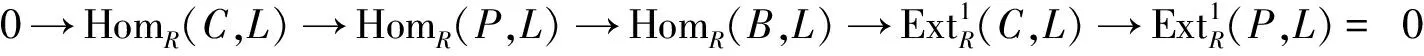
设R是环,M是R-模.若M有如下形式的n-余挠分解0→M→C0→C1→…→Cm-1→Cm→0,其中C0,C1,…,Cm是n-余挠模,则称M的n-余挠维数不超过m,记为cndRM.自然地,M的n-余挠维数cndRM就是M的n-余挠分解的最短长度.当M没有上述形式的n-余挠分解时,则记cndRM=∞.对环R,记

Cn.D(R)=sup{cndRM|∀M∈RM},

称为R的n-余挠整体维数.关于模与环的n-余挠维数的讨论,n=0的情形参见文献[15],一般情形参见文献[10].

定理1.6设L是R-模,则L是内射模当且仅当L是Cn-内射模,且cndRL≤1.

证明若L是内射模,显然有L是Cn-内射模,且cndRL≤1.反之,考虑正合列0→L→E→C→0,其中E是内射模.由条件有cndRC=0,即C是n-余挠模.由文献[16]的推论7.20,此正合列分裂,因此有L是内射模.

回顾环R称为Cn-遗传环,是指每个n-余挠模的商模是n-余挠模,等价于说Cn.D(R)≤1(参见文献[10]).称环R是完全环当且仅当所有R-模是余挠模(参见文献[17]),由定理1.6,可得如下推论.

推论1.7设R是Cn-遗传环,L是R-模,则L是内射模当且仅当L是Cn-内射模.

推论1.8设R是完全环,L是R-模,则L是内射模当且仅当L是C-内射模.

2 环的刻画

下面利用Cn-内射模来刻画环,首先讨论环的半单性,即环R上每个模都是Cn-内射模时,R所具备的一些性质.

定理2.1对环R,以下各条等价:

1) 对任何n≥0,有RM=CnI,即每个R-模是Cn-内射模;

2) 对任何n≥0,有Cn⊆P,即每个n-余挠模是投射模;

3) 存在n≥0,使得RM=CnI,即每个R-模是Cn-内射模;

4) 存在n≥0,使得Cn⊆P,即每个n-余挠模是投射模;

5)R是Artin半单环;

6) 每个余挠模是投射模;

7) 对任何n≥0,有Cn=P;

8) 存在n≥0,使得Cn=P.

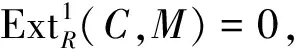
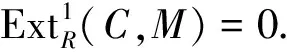
3)⟺4) 类似于1)⟺2).

1)⟹3) 显然.

4)⟹5) 见文献[9]的推论6.5.

5)⟹6) 显然,因为半单环每个模都是投射模.

6)⟹2) 由对任何n≥0,n-余挠模都是余挠模即得.

1)⟹7)⟹8)⟹1) 显然.

下面通过n-余挠模与Cn-内射模的关系来刻画环的性质.

定理2.2设n是非负整数.对环R,以下各条等价:

1)w.gl.dim(R)≤n;

2) Cn⊆CnI,即每个n-余挠模是Cn-内射模;

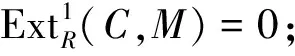
4) 对任何C,M∈Cn,及任何k≥1,有

5) 若cndRX<∞,则对任何M∈Cn有

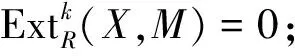
7) Cn⊆Fn,即n-余挠模的平坦维数不超过n.

证明1)⟹2) 由文献[9]的定理6.4,w.gl.dim(R)≤n当且仅当每个n-余挠模是内射模,从而有Cn⊆CnI.

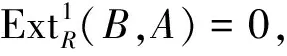
w.gl.dim(R)≤n.

2)⟺3)和2)⟹4)⟹3) 显然.

4)⟹6) 设0→X→C0→C1→…→Cs→0是正合列,其中C0,C1,…,Cs是n-余挠模.由假设,对任何i≥0,及k>0,有

故

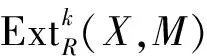
6)⟹5)⟹3) 显然.

3)⟺7) 由(Fn,Cn)是余挠理论即得.

目前已有许多刻画von Neumann正则环和Prüfer整环的方法,也得到诸多结果.借助Cn-内射模的概念,在定理2.2中的分别取n=0和n=1,得到下面关于von Neumann正则环和Prüfer整环的新刻画.

推论2.3对环R,以下各条等价:

1)R是von Neumann正则环;

2) 余挠模是C-内射模;

3) 对任何C,M∈C,有

4) 对任何C,M∈C,及任何k≥1,有

5) 若cdRX<∞,则对任何M∈C,有

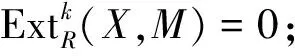
7) C⊆F,即余挠模是平坦模.

推论2.4对整环R,以下各条等价:

1)R是Prüfer整环;

2) 1-余挠模是C1-内射模;

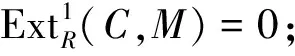
4) 对任何C,M∈C1,及任何k≥1,有

5) 若cdRX<∞,则对任何M∈C1,有

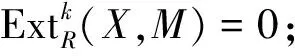
7)C1⊆F1,即1-余挠模的平坦维数不超过1.

对于遗传环的研究已经很普遍,众所周知,可以用内射模的商模是内射模来刻画遗传环;类似的,也可以用Cn-内射模来定义一类广义的遗传环.

定义2.5若Cn-内射模的商模还是Cn-内射模,则称R为CnI-遗传环,C0I-遗传环简称CI-遗传环.

注2.61) 若m≥n≥0,则CnI-遗传环是CmI-遗传环;

2) 对任何n,Artin半单环是CnI-遗传环;

3) 由定理1.6易知R是遗传环当且仅当R是CnI-遗传环且R是Cn-遗传环.

定理2.7对环R,以下各条等价:

1)R是CnI-遗传环;

2) 内射模的商模是Cn-内射模;

3) 每个n-余挠模的投射维数不超过1.

证明1)⟹2) 由内射模是Cn-内射模显然.

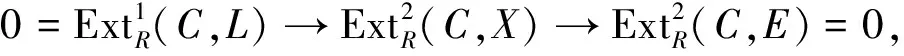
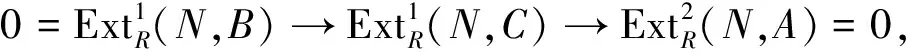
推论2.8若R是CnI-遗传环且每个Cn-内射模是内射模,则R是遗传环.

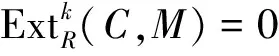
推论2.10对任意的n,Noether的CnI-遗传环是1-Gorenstein环.

证明由定理2.7知R是CnI-遗传环当且仅当n-余挠模的投射维数不超过1,又内射模是n-余挠模,所以内射模的投射维数不超过1,从而R是1-Gorenstein环(详见文献[18]的定理9.1.11).

[1] ENOCHS E E, JENDA O M G. Copure injective modules[J]. Quaestiones Math,1991,14(14):401-409.

[2] MAO L X, DING N Q. Relative copure injective and copure flat modules[J]. Pure and Applied Algebra,2007,208(2):635-646.

[3] ENOCHS E, JENDA O M G. Copure injective resolusions, flat resolvents and dimensions[J]. Comment Math Univ Carolin,1993,34(2):203-211.

[4] DING N Q, CHEN J L. On copure flat modules and flat resolvents[J]. Commun Algebra,1996,24(3):1071-1081.

[5] HARRISON D K. Infinite abelian groups and homological methods[J]. Ann Math,1959,69(2):366-391.

[6] MAO L X, DING N Q. Notes on cotorsion modules[J]. Commun Algebra,2005,33(1):349-360.

[7] MAO L X, DING N Q. Cotorsion modules and relative pure-injectivity[J]. J Australian Math Soc,2006,81(2):225-244.

[8] MAO L X, DING N Q. Relative cotorsion modules and relative flat modules[J]. Commun Algebra,2006,34(6):2303-2317.

[9] MAO L X, DING N Q. Envelopes and covers by modules of finite FP-injective and flat dimensions[J]. Commun Algebra,2007,35(3):833-849.

[10] 熊涛. 模类Fn确定的同调理论及其应用[D]. 成都:四川师范大学,2016.

[11] ENOCHS E E, HUANG Z Y. Injective envelopes and (gorenstein) flat covers[J]. Algebra Represent Theory,2012,15(6):1131-1145.

[12] 任伟,刘仲奎. 余挠模与n-余挠模[D]. 兰州:西北师范大学,2009.

[13] 任伟. 关于cotorsion模与n-cotorsion模[J]. 甘肃科学学报,2008,20(4):33-36.

[14] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006.

[15] MAO L X, DING N Q. The cotorsion dimension of modules and rings[J]. Abelian Groups Rings Modules & Homological Algebra,2006,249:217-233.

[16] ROTMAN J J. An Introduction to Homological Algebra[M]. London:Academic Press,1979.

[17] XU J Z. Flat cover of modules[C]//Lecture Notes of Math,1634. Berlin:Springer-Verlag,1996.

[18] ENOCHS E E, JENDA O M G. Relative Homological Algebra[M]. Berlin:Walter de Gruyter,2000.

[19] 徐龙玉,王芳贵,陈翰林.P-投射模的刻画[J]. 四川师范大学学报(自然科学版),2013,36(4):500-503.

[20] 熊涛,王芳贵,胡葵. 余纯投射模与CPH环[J]. 四川师范大学学报(自然科学版),2013,36(2):198-201.

[21] 谢晋,王芳贵,熊涛. Pn-内射模及其刻画[J]. 四川师范大学学报(自然科学版),2016,39(2):159-162.

[22] 朱占敏. 一类广义遗传环[J]. 纯粹数学与应用数学,2003,19(1):68-71.

[23] IWANAYA Y. On rings with finite self-injective dimension[J]. Tsukuba J Math,1980,4(1):107-113.

[24] GÖBEL R, TRLIFAJ J. Approximations and Endomorphism Algebras of Modules[M]. New York:Walter de Gruyter,2006.

The Characterization on Cn-injective Modules

WANG Xi, WANG Fanggui, HE Ke

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

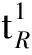
n-cotorsion module; Cn-injective module; Artin semisimple rings; CnI-hereditary ring

2016-11-08

国家自然科学基金(11671283)和教育部博士点专项科研基金(20125134110002)

*通信作者简介:王芳贵(1955—),男,教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:wangfg2004@163.com

O154

A

1001-8395(2017)05-0588-05

10.3969/j.issn.1001-8395.2017.05.004

2010MSC:16D50; 16E10; 16E30

(编辑 余 毅)