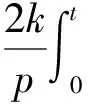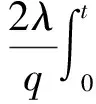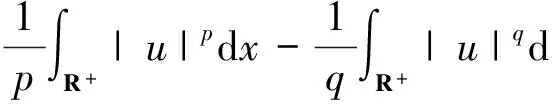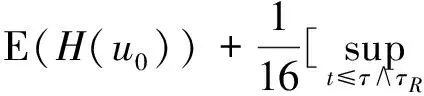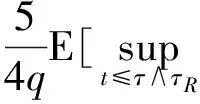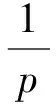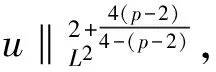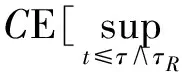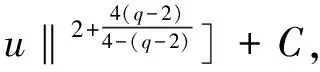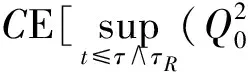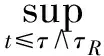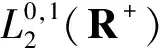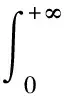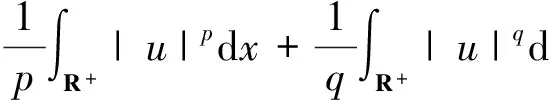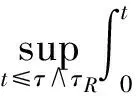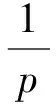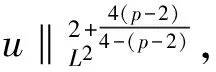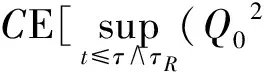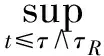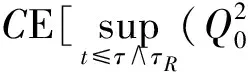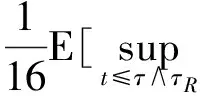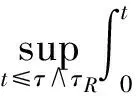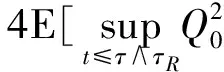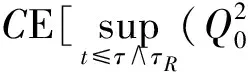带非齐次Dirichlet边界的随机非线性Schrödinger方程解的整体存在性
谢灵燕, 陈光淦
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
带非齐次Dirichlet边界的随机非线性Schrödinger方程解的整体存在性
谢灵燕, 陈光淦*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
研究带有非齐次Dirichlet边界条件且带有加性白噪声的随机非线性Schrödinger方程在H1(R+)空间中的整体解存在性.在偏微分方程理论、泛函分析和随机分析等知识基础上,在质量泛函和能量泛函的基础上引入第三个“桥梁”泛函,通过It公式建立3个泛函之间的关系,最终获得带非齐次Dirichlet边界的随机非线性Schrödinger方程在具有竞争非线性的各种情况下解的有界性,从而获得方程的解的整体存在性.
随机非线性Schrödinger方程; 非齐次Dirichlet边界条件; 加性白噪声; 整体存在性
近年来非线性Schrödinger方程广泛地应用在量子力学、光学、物理、电磁等多个领域中.对于非线性Schrödinger方程,非线性项会影响到解的适定性以及解的爆破行为.目前,非线性Schrödinger方程方面的研究非常多[1-9].随机非线性Schrödinger方程描述光或者波在随机介质中的传播过程,这个过程和时间相关,并且光或者波在传播的过程中会受到不确定因素的干扰.
本文研究同时具有噪声和非齐次的边界条件的非线性Schrödinger方程的整体解,因此,考虑一类带非齐次Dirichlet边界且具有加性白噪声的随机非线性Schrödinger方程
iut=uxx+k|u|p-2u+
x∈R+,t≥0,
(1)
赋予非齐次Dirichlet边界条件
u(0,t)=Q(t),t≥0,
(2)
初值为
u(x,0)=u0(x),
x∈R+,
(3)
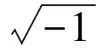
对于带非齐次Dirichlet边界条件的非线性Schrödinger方程的研究,文献[10-11]给出了方程的局部适定性、解的整体存在性以及有限时间内爆破,但此方法不适用于带非齐次Dirichlet边界条件的随机非线性Schrödinger方程相关的问题.对于带齐次边界条件的随机非线性Schrödinger方程,文献[12-13]获得了具有加性噪声或者乘性噪声的系统的局部适定性、解的整体存在性以及爆破,但他们的方法仍然不适用于带非齐次Dirichlet边界条件的随机非线性Schrödinger方程.
本文研究非齐次Dirichlet边界和白噪声同时对非线性Schrödinger方程的影响.为了克服非齐次边界条件和白噪声同时给方程带来的困难,运用偏微分方程理论、泛函分析和随机分析的相关知识,详细地分析系统的特征,在质量泛函和能量泛函的基础上引入第三个“桥梁”泛函,通过It公式建立3个泛函之间的关系,最终获得带非齐次Dirichlet边界的随机非线性Schrödinger方程在具有竞争非线性的各种情况下解的有界性,从而获得方程的解的整体存在性.
1 预备知识
设(Ω,F,P)是一个完备的概率样本空间,并赋予一个域流(Ft)t≥0,另外定义由相互独立的实值布朗运动组成的序列(βe)e∈N,相关于域流(Ft)t≥0,赋予1个希尔伯特正交基(ee)e∈N∈L2(R+),φ∈L2(R+)是有界线性算子.关于W这个维纳过程有
t≥0,x∈R+,ω∈Ω,
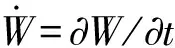
y.
此噪声的相关函数为
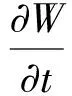
其中
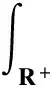
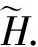
其中(ee)e∈N是空间H上的任意标准正交基.

[14]-[15],有如下局部适定性.
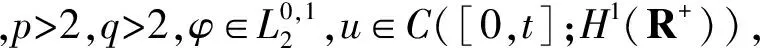
τ*(u0,ω)=+∞,

2 系统的特征分析
现在定义3个泛函,质量泛函
能量泛函
▽u(x)|2dx-
第三个泛函
x.
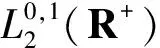
M(u(t))=M(u0)-

(4)
证明对M(u)运用It公式得
M(u(t))=M(u0)+


iλ|u|q-2u)ds+

(5)
其中Mu(u)h是一阶Fréchet微分,h∈H,H是一个Hilbert空间,计算可得
x.
Muu(u)(h1,h2)是二阶Fréchet微分,h1,h2∈H,H是一个Hilbert空间,计算可得
x.
进一步可得:

(6)

ik|u|p-2-iλ|u|q-2u)ds=

(7)

(8)
将(6)~(8)式代入(5)式可得(4)式.
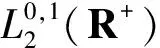


λ|u|q-2u)φee(x)dxdβe(s)-

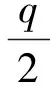
(9)
证明对H(u)运用It公式得


iλ|u|q-2u)ds+

(10)
Hu(u)h是一阶Fréchet微分,h∈H,H是一个Hilbert空间,计算可得
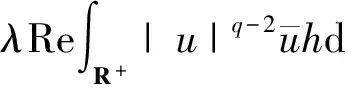
Huu(u)(h1,h2)是二阶Fréchet微分,h1,h2∈H,H是一个Hilbert空间,计算可得
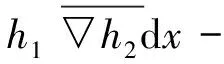
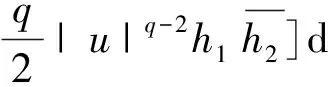
进一步可得:

(11)

iλ|u|q-2u)ds=
(12)



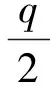
(13)
将(11)~(13)式代入(10)式可得(9)式.
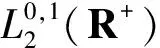

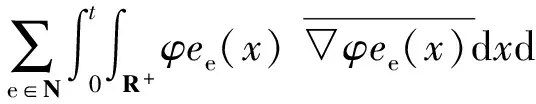
(14)
证明同样用It公式计算得到


ik|u|p-2-iλ|u|q-2u)ds+

(15)
其中Iu(u)h是一阶Fréchet微分,h∈H,H是一个Hilbert空间,可得
其中Iuu(u)(h1,h2)是二阶Fréchet微分,h1,h2∈H,H是一个Hilbert空间,可得
Iuu(u)(h1,h2)=
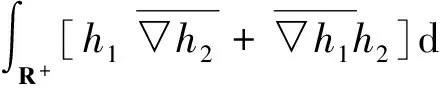
进一步得:

(16)

ik|u|p-2-iλ|u|q-2u)ds=

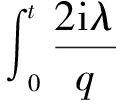
(17)

(18)
将(16)~(18)式代入(15)式可得(14)式.
3 系统的解的整体存在性
3.1非线性项系数k=1,λ=1时方程的解的整体存在性
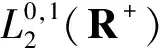
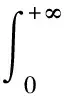
则方程(1)的解整体存在.
证明令
通常习惯用C表示常数.对任给的T0>0,任给停时τ τR=inf{t≤τ*(u0),‖u(t)‖H1(R+)≥R}. 由(14)式得 (19) 对以上等式两边同时取期望,通过Hölder不等式和BDG不等式等工具的处理可得 还可得 ‖u(t)‖2]≤ (21) 当k=1,λ=1时,有 ▽u(x)|2dx- 对H(u)两边同时估计期望,化简得 ‖ux‖2]≤ (22) (23) 由(20)~(23)式,运用Young不等式可得 ‖ux‖2]≤E(H(u0))+ (24) 将(21)式代入(24)式得 ‖ux‖2]≤E(H(u0))+ (25) 3.2非线性项系数k=1,λ=-1时方程的解的整体存在性 则方程(1)的解整体存在. 证明令 对任给的T0>0,任给停时τ τR=inf {t≤τ*(u0),‖u(t)‖H1(R+)≥R}. 当k=1,λ=-1有 ▽u(x)|2dx- 对H(u)两边同时估计期望可得 ‖ux‖2]≤E(H(u0))+ (26) 由Gagliardo-Nirenberg和Young不等式可得 (27) 将(20)、(21)和(27)式代入(26)式得 ‖ux‖2]≤E(H(u0))+ (28) 在(20)和(21)式的基础上,运用Young不等式可得 ‖ux‖2]≤E(H(u0))+ (29) 3.3非线性项系数k=-1,λ=-1时方程的解的整体存在性 则方程(1)的解整体存在. 证明令 对任给的T0>0,任给停时τ τR=inf{t≤τ*(u0),‖u(t)‖H1(R+)≥R}. 当k=-1,λ=-1时有 ▽u(x)|2dx+ 对H(u)两边同时估计期望得 ‖ux‖2]≤E(H(u0))+ (30) 在(20)和(21)式基础上,对(30)式用Young不等式进一步计算有 ‖ux‖2]≤E(H(u0))+ (31) 参考文献 [1] UEDA T, KATH W L. Dynamics of optical pulses in randomly birefrengent fibers[J]. Physica D Nonlinear Phenomena,1992,55(1/2):166-181. [2] CHEN G G, ZHANG J. Remark on global existence for the superctitical nonlinear Schrödinger equation with a harmonic potential[J]. J Math Anal Appl,2006,320(4):591-598 [3] CHEN G G, DUAN J Q, ZHANG J. Geometric shape of invariant manifolds for a class of stochastic partial differential equations[J]. J Math Phys,2011,52(7):072702. [4] 舒级,张健. 一类带无界势的非线性Schrödinger方程的整体性[J]. 四川师范大学学报(自然科学版),2005,28(4):20-22. [5] 步起跃. 半无穷直线上的非线性薛定谔方程[J]. 数学年刊,2000,21(4):437-448. [6] CARROL R, BU Q Y. Solution of the forced nonlinear Schrödinger equation using PDE techniques[J]. Appl Anal,1991,41(1):33-51. [7] BRZEZNIAK Z, PESZAT S. Space-time continuous solutions to SPDE’s driven by a homogeneous Wiener process[J]. Studia Math,1999,123(1):261-299. [8] BOUARD D A, DEBUSSCHE A. A Finite time blow-up in the additive supercritical stochastic nonlinear Schrödinger euqation:the real noise case[J]. Contemp Math,2002,301(4):183-194. [9] BANG O, CHRISTIANSEN P L. White noise in the two-dimensional nonlinear Schrödinger euqation[J]. Appl Anal,1995,57(7):3-15. [10] BU C. Forced cubic Schrödinger equation with Robin boundary data:continuous dependency result[J]. ANZIAM J,2000,41(3):301-311. [11] GUO B L, WU Y H. Global existence and nonexistence of the solution of a forced nonlinear Schrödinger equation[J]. I Math Phys,1995,36(7):3479-3483. [12] BOUARD D A, DEBUSSCHE A. The stochastic nonlinear Schrödinger equation inH1(Rn)[J]. Stochastic Anal Appl,2003,21(5):97-126. [13] BOUARD D A, DEBUSSCHE A. On the effect of a noise on the solutions of the focusing supercritical nonlinear Schrödinger Equations[J]. Probab Theory Related Fields,2002,123(1):76-96. [14] BU Q. On well-posedenss of the forced NLS equation[J]. Appl Anal,1992,46(1):219-239. [15] STRAUSS W. An inhomogeneous boundary value problem for nonlinear Schrödinger equation[J]. J Diff Eqns,2001,173(1):79-91. Global Existence of a Stochastic Nonlinear Schrödinger Equation with Inhomogeneous Dirichlet Boundary Value XIE Lingyan, CHEN Guanggan (CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan) We study the global existence of solutions in the energy spaceH1(R+) for the stochastic nonlinear Schrödinger equation with Dirichlet boundary value. Based on the partial differential equations theories, functional analysis and stochastic analysis, we introduce the third bridge functional on the basis of quality functional and energy functional and establish the relationship among these three functionals by Itformula. We get the boundedness of the solution of the the stochastic nonlinear Schrödinger equation with inhomogeneous Dirichlet boundary value, additive white noise and competitive nonlinear terms in each cases and finally obtain the global existence of solution of the equation. stochastic nonlinear Schrödinger equation; inhomogeneous Dirichlet boundary value; white noise; global existence 2015-04-08 国家自然科学基金(11347102)和四川省杰出青年带头人培育计划基金(2012JQ0041) *通信作者简介:陈光淦(1978—),男,教授,主要从事随机偏微分方程的研究,E-mail:chenguanggan@hotmail.com O159 A 1001-8395(2017)05-0593-07 10.3969/j.issn.1001-8395.2017.05.005 2010MSC:60H15; 35L05; 60H30 (编辑 郑月蓉)