双参数扰动下有理函数的线性化

丁志瑛, 周 吉

(1. 成都东软学院, 四川 成都 611844; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

双参数扰动下有理函数的线性化

丁志瑛1, 周 吉2*

(1. 成都东软学院, 四川 成都 611844; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

利用多复变函数理论和Geyer的思想,通过对有理函数进行适当的双参数扰动,给出Douady猜想成立的一个充分条件.

线性化; Weierstrass预备定理; 有理函数

1 引言及预备知识

φ·R·φ-1(z)=λ(z-p),

称R在p点可线性化.人们发现:无理中性不动点p是属于函数R的Fatou集等价于该函数在p点是可线性化,并且当p属于Fatou集时,包含p点的Fatou分支是单连通的,该Fatou分支称为Siegel盘,p为Siegel盘的中心[1].因此，判定无理中性不动点是属于Fatou集还是属于Julia集是一个“中心”问题，已得到许多数学家的关注.

目前已知:上述问题与α的数论性质有密切的联系.如果α满足0<α<1是无理数,pn/qn是第n个渐进分数,即α的连分数表示的一个截断,且

则称α为Brjuno数,用B表示所有这些Brjuno数组成的集合.A.D.Brjuno[2]得到:当α是Brjuno数时,R在不动点p处是可线性化的.这个结论改进了C.L.Siegel的结果[3].后来,J.C.Yoccoz[4]得到Brjuno的这个条件对二次多项式

Pλ(z)=λz+z2,λ=e2πiαz

来说还是必要的.但对一般的有理函数而言,这个条件是否也是必要的还不得而知.1978年,A. Douady给出了猜想[5]：设R是度大于1的有理函数,如果α不满足Brjuno条件,则R在不动点p处不可线性化.

J.C.Yoccoz的结果[4]说明:对于二次多项式A.Douady猜想是真的.迄今为止,对于三次多项式该猜想是否成立仍然不知.L.Geyer[6]考虑了一些特殊的多项式类:

Pc,d=zd+c,d≥2,c∈C,

和

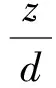
对于这些多项式Douady猜想是真的.

L.Geyer[6]借助于扰动多项式的二次项系数,将一般多项式转化成二次多项式,再利用J.C.Yoccoz[4]的结论来考虑Douady猜想.

引理1.1设δ>0,对所有的|a|<δ,函数

fa(z)=f(z)+az2g(z)

在0点都可线性化,其中f、g在原点是解析的,

f(0)=0,f′(0)=λ=e2πiα,

α∈RQ,g(0)≠0,

则二次多项式Pλ(z)=λz+z2也可线性化,所以α∈B.

L.Geyer[6]用的是单参数扰动,但是要研究有理函数的线性化问题,仅用单参数是不够的,因为对于单复变函数,唯一性定理说明了函数的零点是孤立的.为了研究有理函数,需要借助多复变函数理论.

接下来,本文将对有理函数进行适当的双参数扰动,从而证明Douady猜想是真的.

2 主要结果

利用多复变函数理论研究有理函数,得到如下结果.

定理2.1设δ>0,R(z)为有理函数,且

R(0)=0,R′(0)=λ,λ=e2πiα,

函数族Qa,b(z)定义为

Qa,b(z)=R(z)+A2(a,b)z2+A3(a,b)z3,

其中A2(a,b)、A3(a,b)在点(0,0)的某个邻域内解析,

A2(0,0)=A3(0,0)=0,

A2(a,b)A3(a,b)≠0,a,b≠0.

如果当|a|,|b|<δ时,Qa,b(z)在0点都可线性化,则二次多项式Pλ(z)=λz+z2也可线性化.

证明首先,分3种情形证明如下结论:在定理的假设条件下,存在r>0,使得对每个γ∈C,|γ|

情形1假如对任意a,|a|<δ,有A3(a,0)=0,则A2(a,0)是一个非常值解析映射,这表明了A2(a,0)是开映射,即集合{A2(a,0)∈C||a|<δ}是一个包含0的开集.由此,该集合包含了以0为中心,r为半径的圆盘.因此,所证结论成立.

情形2假如对任意a,|a|<δ,有A3(a,0)不恒等于0且0是A3(a,0)的一阶零点,则由Taylor定理知,在以0为中心,r为半径的开圆盘Dr(0)上,存在一解析函数a(b),使得当b∈Dr(0)时,A3(a(b),b)=0,则A2(a(b),b)在Dr(0)上是解析的,因此,A2(a(b),b)将Dr(0)映成一个包含0的开集.从而所证结论成立.

情形3假如对任意a,|a|<δ,有A3(a,0)不恒等于0且0是A3(a,0)的d>1阶零点.

引理2.2(Weierstrass预备定理)设函数f(a,b)在(0,0)的某个邻域内全纯,函数f(a,0)以0为k>0阶零点且不恒为零,则在(0,0)的某个邻域U内f可表示为

f(a,b)=P(a,b)h(a,b),

其中,h在U上全纯,

h(0,0)≠0,

P(a,b)=ak+gk-1(b)ak-1+…+g0(b),

gi(b)在0附近解析,

gi(0)=0,i=0,1,…,k-1.

形如上述引理中的多项式P(a,b)称为关于a的k次Weierstrass多项式.

对情形3,由Weierstrass预备定理知:存在在(0,0)附近解析的函数H(a,b)和Weierstrass多项式

G(a,b)=ad+k1(b)ad-1+…+kd(b),

使得

A3(a,b)=G(a,b)H(a,b),

从以上讨论发现,对γ∈C,|γ|

Qa,b(z)=R(z)+A3(a,b)z3+A2(a,b)z2=R(z)+γz2.

因此,每个多项式

Qγ(z):=R(z)+γz2, |γ|

都可以线性化.由引理1.1知二次多项式Pλ(z)=λz+z2可以线性化.

因此,如果一个有理函数对二次和三次项的系数作适当的扰动,仍然是可线性化的,则可以得到相应的二次多项式Pλ(z)是可线性化,因而Douady猜想是真的.这样,验证该猜想可转化为验证有理函数是否满足该定理的条件.

[1] MILNOR J. Dynamics in One Complex Variable[M]. Princeton:Princeton University Press,2006.

[2] BRJUNO A D. Analytical form of differential equations[J]. Trans Moscow Math Soc,1971,25:131-288.

[3] SIEGEL C L. Iteration of analytic functions[J]. Ann Math,1942,43:607-612.

[4] YOCCOZ J C. Theorem de Siegel, nombres de Brjuno et polynomials quadratiques[J]. Asterisque,1995,231:3-88.

[5] DOUADY A. Disques de Siegel et anneaux de Herman[J]. Sém Bourbaki,1986/1987,39:151-172.

[6] GEYER L. Siegel discs, Herman rings and the Arnold family[J]. Trans Am Math Soc,2001,353(9):3661-3683.

[7] AHLFORS L V. Complex Analysis[M]. New York:McGraw-Hill,1979.

[8] FRITZSCHE K, GRAUERT H. From Holomorphic Functions to Complex Manifolds[M]. New York:Springer-Verlag,2002.

[9] SHABAT B V. Introduction to complex analysis part II: functions of several variables[C]//Translations of Mathematical Monographs. Providence IR:Am Math Soc,1992.

[10] STEVEN G K. The Hartogs extension phenomenon redux[J]. Complex Variables and Elliptic Equations,2011,53(4):343-353.

Linearization of Rational Functions with Two-parameter Perturbation

DING Zhiying1, ZHOU Ji2

(1.ChengduNeusoftCollege,Chengdu611844,Sichuan; 2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

In this paper, a sufficient condition for Douady conjecture is proposed via a perturbation of two-parameters on rational functions, which is based on complex analysis of several variables and idea of Geyer.

linearizability; Weierstrass preparation theorem; rational functions

2016-02-04

国家自然科学基金(11371266)、教育部博士点专项基金(20095134110001)和四川省应用基础研究项目(07JY029-013)

*通信作者简介:周 吉(1963—),男,教授,主要从事复分析的研究,E-mail:zhouji@sicnu.edu.cn

Q949O174.5

A

1001-8395(2017)05-0585-03

10.3969/j.issn.1001-8395.2017.05.003

2010MSC:37F50

(编辑 周 俊)